Applied Survival Analysis

Chapter 10 - Competing/Semi-Competing Risks

Lu Mao

lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

Cause-specific hazard and cumulative incidence
Non- and semi-parametric methods
Analysis of bone marrow transplantation study
Semi-competing risks and examples

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\cc}{{\rm c}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Basic Quantities

Definition and Examples

Competing risks
- Definition: multiple types of failures, occurrence of one precludes others
  - Multiple latent risks competing with each other for first occurrence
- Examples: different causes of death

Defining feature
- One failure per subject
- Less info than multivariate failure times
- Implications for analysis and interpretation

Outcome Data & Identifiability

Target of inference: $(T, \Delta)$
- $T$: time to failure
- $\Delta \in \{1, \ldots, K\}$: type/cause of failure (categorical)

Multivariate perspective
- A conceptual framework \[\begin{equation}\label{eq:cmpr:mult} T=\min(T_1,\ldots, T_K) \hspace{1mm}\mbox{ and } \hspace{1mm}\Delta=\arg\min_{k=1,\ldots, K} T_k \end{equation}\]
  - $T_k$: time to $k$th latent risk $(k=1,\ldots, K)$ in absence of other risks
  - Competing risks $=$ partially observed multivariate failure times
- Identifiability: net distribution of latent $T_k$ not recognizable from $(T, \Delta)$
  - unless under unrealistic assumption of mutual independence of the $T_k$

Two Approaches

Two ways to characterize $(T, \Delta)$
- Cause-specific hazard
- Cumulative incidence (Sub-distribution)

Cause-specific hazard (CSH) \[\begin{equation}\label{eq:cmpr:cs_hazard} \dd\Lambda_k^\cc(t)=\pr(t\leq T<t+\dd t, \Delta=k\mid T\geq t) \end{equation}\]
- Interpretation: instantaneous incidence of $k$th risk given overall “survival”
- Example: $\dd\Lambda_1^\cc(t)=$ incidence rate for CV death among survivors at $t$
  - $k =1$: CV death; $k =2$: other causes of death
- Overall hazard: $\dd\Lambda(t)=\pr(t\leq T<t+\dd t \mid T\geq t) = \sum_{k=1}^K \dd\Lambda_k^\cc(t)$

Cause-Specific Hazard

Limitations
- The cumulative CSH $\Lambda_k^\cc(t)$ not a meaningful quantity
- $\exp\{-\Lambda_k^\cc(t)\}$ not a survival function of any kind

Correspondence with “net hazard”
- Under (unrealistic) mutual independence of the latent $T_k$
- Hazard of $T_k$ identifiable and equal to $\Lambda_k^\cc(t)$
- Not recommended

Cumulative Incidence

Cumulative incidence function (CIF) \[ F_k(t)=\pr(T\leq t, \Delta=k) \]
- Interpretation: probability of failure from $k$th risk in presence of other risks
- Marginal quantity, easy to interpret (a real-world probability)
- $F(t)=\pr(T\leq t) = \sum_{k=1}^K F_k(t)$ (sub-distribution functions)

Relationship
- CSH in terms of CIF (for a particular risk, no one-to-one correspondence) \[\begin{equation}\label{eq:cmpr:correspond} \dd\Lambda_k^\cc(t)=\frac{\dd F_k(t)}{1-\sum_{l=1}^K F_l(t-)} \end{equation}\]

CSH vs CIF

Example: effect on CSH may not align with CIF
- Treatment: $\Lambda_1^\cc(t)=\Lambda_2^\cc(t)=3t$
- Control: $\Lambda_1^\cc(t)=2t$ and $\Lambda_2^\cc(t)=t$

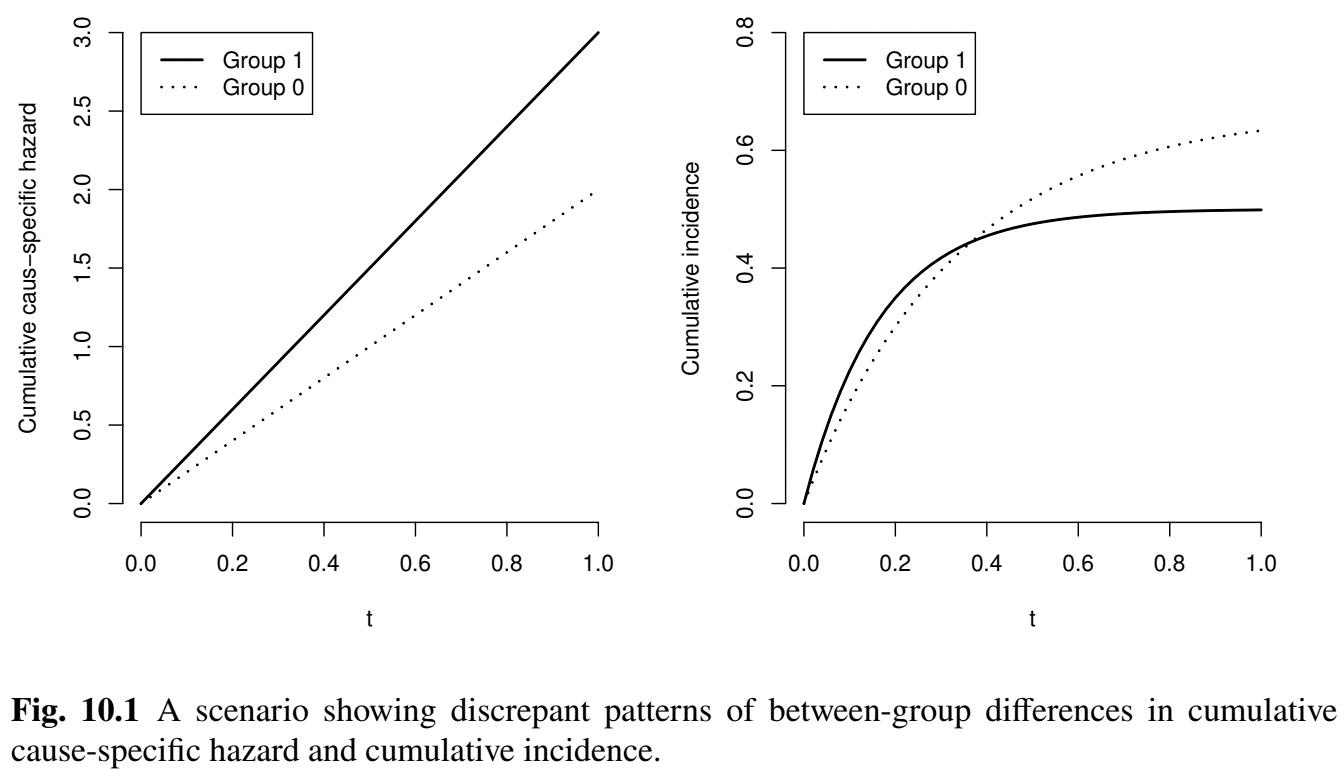
Comparison of Functions

CSH vs net hazard vs CIF

Methods for Competing Risks

Observed Data

A random $n$-sample \[(X_i, \delta_i, Z_i), \,\,\, i=1,\ldots, n\]
- $X=T\wedge C$
- $\delta=\Delta I(T\leq C)$ (0: censored; $k$: observed $k$th risk, $k=1,\ldots, K$)
- $C$: independent censoring time
- $Z$: covariates
- $N_{ki}(t)=I(X_i\leq t, \delta_i=k)$: Observed counting process for $k$th risk

Cause-Specific Hazard Models (I)

Proportional cause-specific hazards \[\begin{equation}\label{eq:cmpr:ph_csh} \pr(t\leq T<t+\dd t, \Delta=k\mid T\geq t, Z)=\exp(\beta_k^\T Z)\dd\Lambda_{k0}(t) \end{equation}\]
- A model on “survivors” (those who have not failed from any risk)
- $\beta_k$: log-hazard ratios for $k$th risk in survivors

Estimation
- Partial likelihood score for $k$th risk \[ U_{nk}(\beta_k)=\Pn\int_0^\infty\left\{Z_i-\frac{\sum_{j=1}^n I(X_j\geq t)Z_j\exp(\beta_k^\T Z_j)}{\sum_{j=1}^n I(X_j\geq t)\exp(\beta_k^\T Z_j)}\right\}\dd N_{ki}(t) \]
  - Essentially treating non-$k$ risks as censoring
  - Easy to implement in survival::coxph() (status == k)

Cause-Specific Hazard Models (II)

Under (unrealistic) independence of the latent $T_k$
- Proportional cause-specific hazards $\Longleftrightarrow$ proportional net hazards
- Frailty to relax independence
- Not recommended
  - Non-identifiability
  - Non-interpretability

Log-rank test
- Risk-specific log-rank statisic with other risks treated as censoring
- “Kaplan-Meier” doesn’t work $\to$ estimand $\exp\{-\Lambda_k^\cc(t)\}$ is non-quantity
- Competing-risks equivalent of KM is Gray (1988) estimator of $F_k(t)$

CIF: Nonparametric Estimation

Decomposition of $F_k(t)$ \[\begin{equation*} \dd F_k(t)=S(t-)\dd\Lambda_k^\cc(t) \end{equation*}\]
- $S(t-)=\pr(T\geq t)$: By KM estimator $\hat S(t-)$ for overall failure
- $\dd\Lambda_k^\cc(t)$: By Nelsen-Aalen estimator (non-$k$ risks as censoring) \[ \dd\hat\Lambda_k^\cc(t)=\frac{\sum_{i=1}^n\dd N_{ki}(t)}{\sum_{i=1}^n I(X_i\geq t)} \]

Gray estimator \[\begin{equation*} \hat F_k(t)=\int_0^t \hat S(u-)\dd\hat \Lambda_k^\cc(u) \end{equation*}\]

CIF: Sub-Distribution Hazard

Sub-distribution hazard (SDH) \[\begin{equation}\label{eq:cmpr:sdh} \dd\Lambda_k(t)=\pr(t\leq T_k^*<t+\dd t\mid T_k^*\geq t) \end{equation}\]
- Time to $k$th risk in presence of other risks \[ T_k^*=T\cdot I(\Delta=k)+\infty\cdot I(\Delta\neq k) \]
  - $F_k(t)=\pr(T_k^*\leq t)$
- Interpretation: incidence of $k$th risk given not failing from it
- Easier to work with hazard-like functions (unbounded)
- Correspondence with CIF \[\begin{equation}\label{eq:cmpr:subdist} F_k(t)=1-\exp\{-\Lambda_k(t)\} \end{equation}\]
- Model/test on SDH $\Longleftrightarrow$ Model/test on CIF

CIF: Gray’s Test

Discrete version ($k$th risk) \[ \dd\Lambda_k(t)=\frac{\dd F_k(t)}{1-F_k(t-)} \]

Log-rank-type test
- Testing $H_0: F_{k1}(t)=F_{k0}(t)$ \[\begin{equation}\label{eq:cmpr:gray_tests} \int_0^\infty W_k(t)\big\{\dd\hat\Lambda_{k1}(t)-\dd\hat\Lambda_{k0}(t)\big\} \end{equation}\]
- $\hat\Lambda_{ka}(t)$: Gray’s CIF plug-in estimator for SDH in group $a$ $(a=1, 0)$
- $W_k(t)$: Weight function
- Extensions: multi-group, stratification, etc.

CIF: Fine-Gray Regression

Proportional sub-distribution hazards (Fine and Gray, 1999) \[\begin{equation}\label{eq:cmpr:fg} \pr(t\leq T_k^*<t+\dd t\mid T_k^*\geq t, Z)=\exp(\beta_k^\T Z)\dd\Lambda_{k0}(t) \end{equation}\]
- $\beta_k$: log-hazard ratios for $k$th risk in entire population (under other risks)
- Estimation and inference: partial-likelihood score with IPCW to address dependent censoring by other risks

Target populations
- Cause-specific hazard: survivors
- Sub-distribution hazard: all, including those who have failed from other causes

Software: `cmprsk::cuminc()`

Basic syntax for Gray’s estimator & test

obj <- cuminc(ftime, fstatus, group, strata, rho = 0)

Input
- (ftime, fstatus): $(X, \delta)$
- group: group variable (optional); strata: strata variable (optional)
- rho: $\rho$ in weight $W_k(t)=\{1 - \hat F_k(t)\}^\rho$ (HF $G^\rho$ family)
Output: a list
- obj$Tests: tests results on each risk
- obj$"a k": CIF estimates for $k$th risk in group $a$
  - time: $t$; est: $\hat F_k(t)$; var: $\hat\var\{\hat F_k(t)\}$

Software: `cmprsk::crr()` (I)

Basic syntax for Fine-Gray model

obj <- crr(ftime, fstatus, cov1, failcode = k)

Input
- (ftime, fstatus): $(X, \delta)$; cov1: $Z$
- failcode = k: models $k$th risk

Output: a list of class crr
- obj$coef: $\hat\beta_k$; obj$var: $\hat\var(\hat\beta_k)$
- obj$uftime: $t$; obj$bfitj: $\dd\hat\Lambda_{k0}(t)$

Software: `cmprsk::crr()` (II)

Prediction of CIF by Fine-Gray model
- obj: a crr object for fit model
- z: new covariate data

# --- Method 1: use predict.crr() 
obj_pred <- predict(obj, z)

# --- Method 2: manual calculation
beta <- obj$coef
Lambda <- cumsum(obj$bfitj)
time <- obj$uftime
## Calculate CIF based on FG model
cif <- 1- exp(- exp(sum(beta * z)) * Lambda)
## Same as obj_pred from Method 1
obj_pred <- cbind(time, cif)

Software: `tidycmprk` Package (I)

Tidy competing risks analysis
- Wraps around cmprsk functions
- Formula-based interface $+$ Tidy output
- Integrated with ggsurvfit and gtsummary
Main functions
- Nonparametric analysis
  - tidycmprsk::cuminc(): model fitting
  - tidycmprsk::tbl_cuminc(): tabulation of CIF estimates
  - ggsurvfit::ggcuminc(): plotting of CIF estimates
- Fine-Gray regression
  - tidycmprsk::crr(): model fitting
  - gtsummary::tbl_regression(): regression table

Software: `tidycmprk` Package (II)

Sample code

# Compute and test on cumulative incidence function (CIF) -------------------
obj_cif <- tidycmprsk::cuminc(Surv(time, status) ~ group, data = df)
# Tabulate CIF estimates with 95% CI at specific times
tbl_surv <- tidycmprsk::tbl_cuminc(
    x = obj_cif,                     # Provide fitted object
    times = seq(12, 120, by = 36),   # Time points for CIF
    outcomes = c("1", "2"),          # Specify risks to include
) 
# Create group-specific CIF plot
ggcuminc(obj_cif, outcome = c("1", "2"))  # Specify risks to include

# Fine-Gray regression for risk "k" -----------------------------------------
obj_fg <- tidycmprsk::crr(Surv(time, status) ~ covariates, 
                           data = df, failcode = "k")
# Tabulate regression results
tbl <- tbl_regression(obj_fg, exponentiate = TRUE)

Bone Marrow Transplant Study

Study Information

Population
- 864 multiple-myeloma patients undergoing allo-HCT cell transplantation
Endpoints: time from surgery to
- Treatment-related mortality (TRM; death in remission)
- Relapse of leukemia
Risk factors
- Cohort indicator (years 1995–2000 or 2001–2005)
- Type of donor (unrelated or HLA-identical sibling)
- History of a prior transplant
- Time from diagnosis to transplantation (<24 months, or ≥ 24 months)

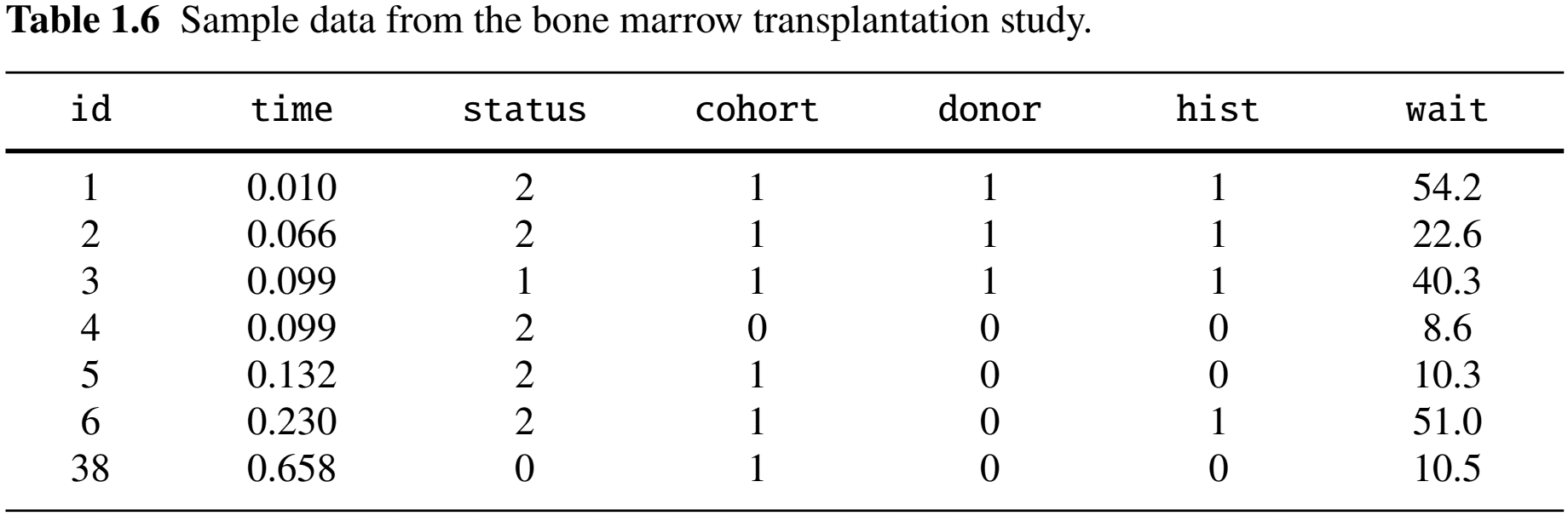
Study Data

Data format

head(cibmtr)
#>    time status cohort donor hist wait
#> 1 0.010      2      1     1    1    1
#> 2 0.066      2      1     1    1    0
#> 3 0.099      1      1     1    1    1
#> ...

CIF by Donor Type (I)

Estimation/testing by donor type

obj_cif <- tidycmprsk::cuminc(Surv(time, status) ~ donor, data = df)
obj_cif # Print results
#> ...
#> • Tests
#> outcome   statistic   df     p.value    
#> Relapse   17.3        1.00   <0.001     
#> TRM       12.3        1.00   <0.001

# Summarize CIF estimates at specific times 
tbl_surv <- tbl_cuminc(
    x = obj_cif,                     # Provide the fitted object
    times = seq(12, 120, by = 36),   # Time points for CIF
    outcomes = c("Relapse", "TRM"),  # Specify risks to include
    label_header = "{time} months"   # Column label format
) 
tbl_surv

CIF by Donor Type (II)

Table created by tbl_cuminc()

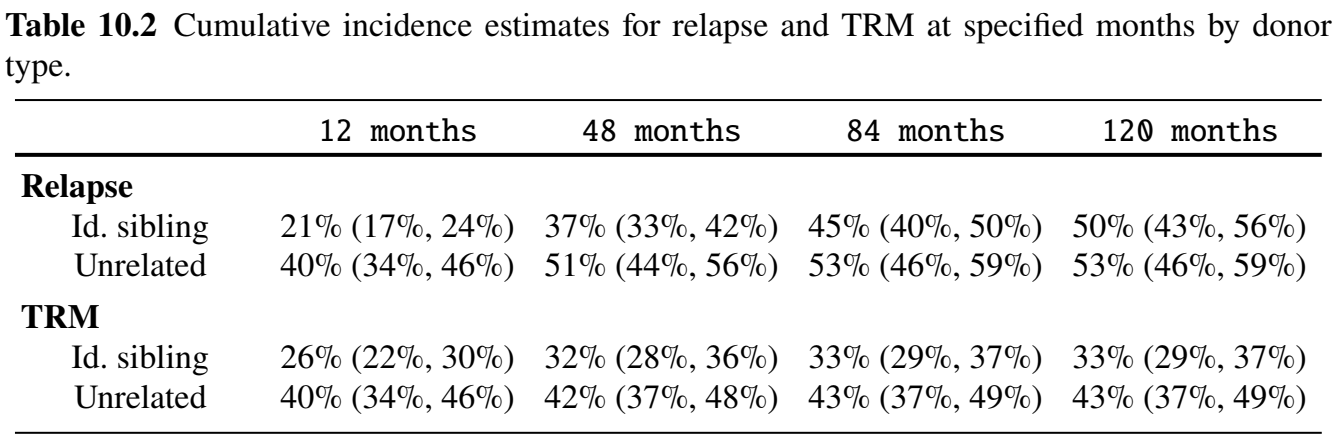
CIF by Donor Type (III)

Graphics

obj_cif |> ggcuminc(outcome = c("Relapse", "TRM")) # + ggplot2 formatting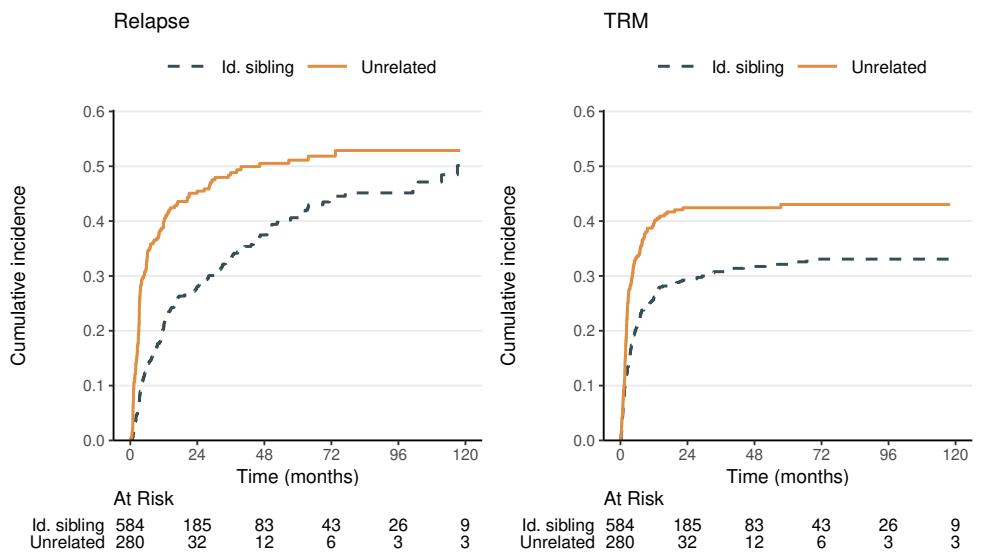

Regression Analysis

Semiparametric regression
- Proportional cause-specific hazard
- Proportional sub-distribution hazard (FG)

# Change k
k <- 1
#--- proportional cause-specific hazards -----------------------------
obj.cs <- coxph(Surv(time, status == k) ~ cohort + donor + hist + wait,
                data = cibmtr)

#--- Fine and Gray --------------------------------------------------
obj.fg <- crr(cibmtr$time, cibmtr$status, cibmtr[, 3:6], failcode = k)

Regression Results

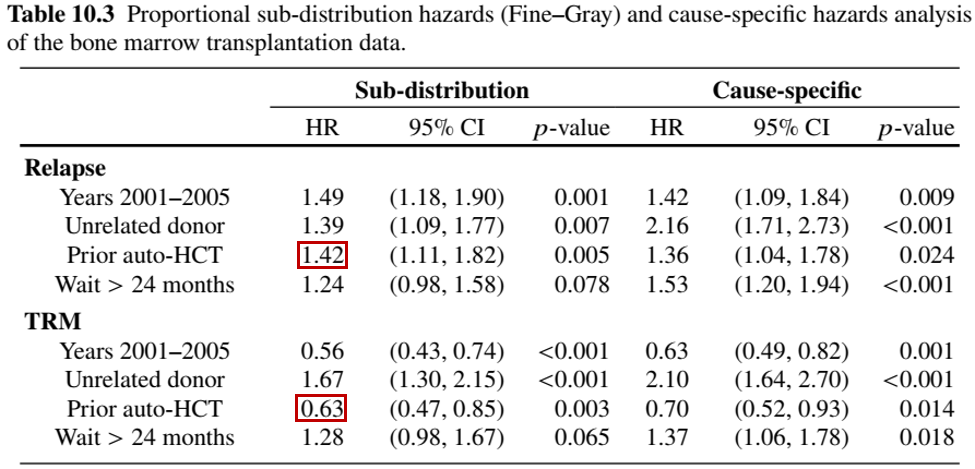
Differential effects of prior surgery
- Relapse: increases risk by $42\%$
- TRM: decreases risk by $1-0.63 = 37\%$

Semi-Competing Risks

Definition and Examples

Semi-competing risks
- Terminal event (competing): death
- Non-terminal events (non-competing): hospitalization, relapse, etc.

Examples
- Death + relapse of cancer (German breast cancer study)
- Death terminates nonfatal event but not vice versa

Methods
- Marginal: cumulative incidence/frequency
- Frailty (Ch. 8); Multistate (Ch. 12); Composite (Ch. 13)

Data and Identifiability

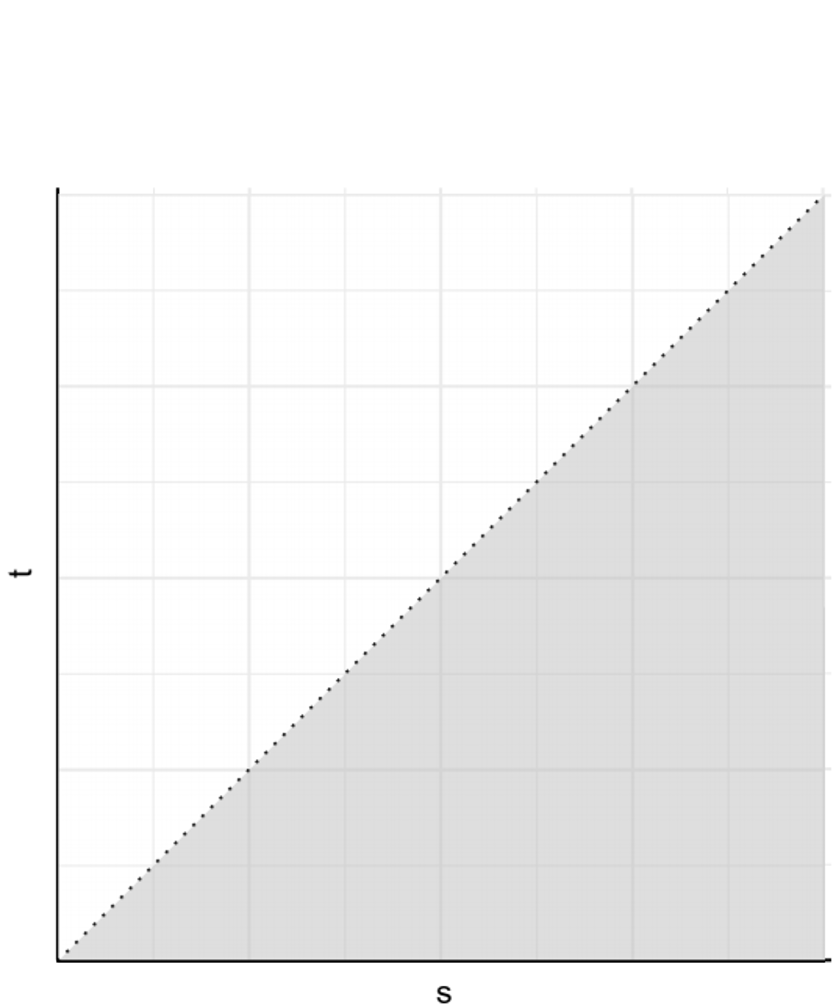
Target of inference: $(T, D)$
- $T$: time to nonfatal event
- $D$: time to death
- Joint distribution \[H(s, t)=\pr(D>s, T>t)\]
- Identifiable region: $\{(s, t):0\leq t\leq s<\infty\}$
  - Possible nonfatal $\to$ death, not vice versa

Bivariate Analysis

Marginal models
- Death: univariate event (KM, log-rank, Cox)
- Nonfatal event
  - Cause-specific risk (treating death as censoring)
  - cumulative incidence (Gray, FG)

German breast cancer study
- Nonfatal event: relapse of cancer (status == 1)
- Death: overall mortality (status == 2)

gbc <- read.table("Data//German Breast Cancer Study//gbc.txt") |>
   mutate(age40 = (age > 40) + 0) # create age40: I(age > 40)

Bivariate Analysis - GBC Example (I)

Data

gbc
#    id      time status hormone age meno size grade nodes prog estrg age40
# 1   1 43.836066      1       1  38    1   18     3     5 1.41  1.05     0
# 2   1 74.819672      0       1  38    1   18     3     5 1.41  1.05     0
# 5   3 41.934426      1       1  47    1   30     2     1 4.22  0.89     1
# 6   3 47.737705      2       1  47    1   30     2     1 4.22  0.89     1

Analysis
- Death (subset to status != 1)
  - Standard Cox: coxph(Surv(time, status == 2) ~ covariates)
- Relapse (subset to first row for each id)
  - Cause-specific hazard: coxph(Surv(time, status == 1) ~ covariates)
  - Sub-distribution hazard: tidycmprk::crr(Surv(time, status) ~ covariates, failcode = "1")

Bivariate Analysis - GBC Example (II)

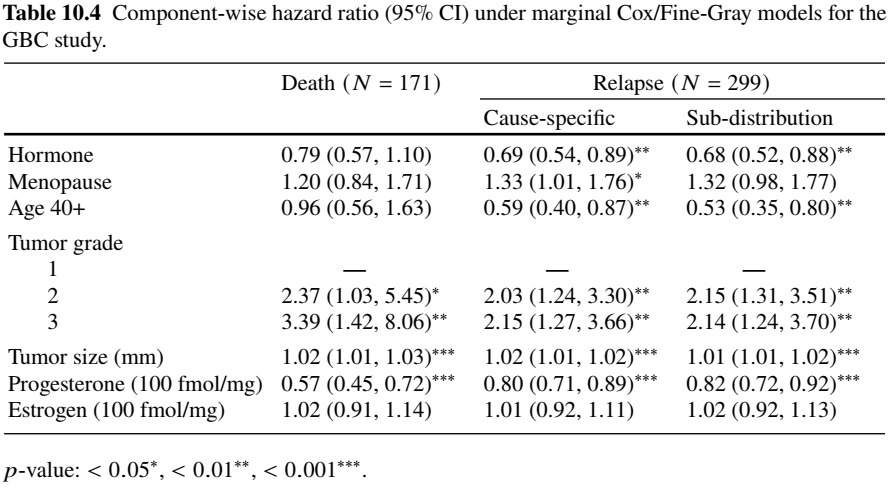
Regression results
- Relapse: cause-specific $\approx$ sub-distribution—few deaths (21) before relapse
- Age effect: driven by relapse

Recurrent Events

Outcome data: $\{N^*(\cdot), D\}$
- $N^*(t)$: number of recurrent events in presence of death
  - Repeated tumor occurrences/hospitalizations before death ($\dd N^*(t)\equiv 0$ for $t>D$)
- Treating $D$ as censoring (AG/LWYY) $\to$ cause-specific event rate \[E\{\dd N^*(t)\mid D\geq t\}\]
  - Incidence rate in survivors

Cumulative frequency
- Mean function in overall population, dead or alive \[ \mu(t)=E\{N^*(t)\} \]
- Extension of cumulative incidence

Marginal Approaches

Methods for cumulative frequency
- Gray-type nonparametric estimator/test (Ghosh and Lin, 2000)
- Proportional CF model (Fine-Gray-type) (Ghosh and Lin, 2002) \[\begin{equation}\label{eq:cmpr:pcf} E\{N^*(t)\mid Z\}=\exp(\beta^\T Z)\mu_0(t) \end{equation}\]
- Higher death rate can reduce CF

Joint analysis with mortality
- Ghosh-Lin for recurrent events $+$ Cox/log-rank for death
- $\chi^2$ test with 2 d.f.

Alternative: shared-frailty models

Software: `rccf2::rccf()`

Two-sample estimation/testing of CF

devtools::install_github("lmaowisc/rccf2")
library(rccf2) # Load package
obj <- rccf(id, time, status, trt) # Fit model

Input
- id: subject ID; trt: binary treatment group
- time: event time; status: event status (1: nonfatal; 2: death; 0: censoring)

Output
- obj$u1, obj$u2: Estimates of group-specific $\mu(t)$ as a function of $t$ (obj$t).
- obj$pLR, obj$pD, obj$pjnt: $p$-values for tests on $\mu(t)$, death, and jointly

Example: Bladder Tumor Study (I)

Bladder cancer trial (Byar, 1980)
- Treatment groups: thiotepa ($n=38$) vs placebo ($n=48$)
- Endpoints: tumor recurrences and death

Example: Bladder Tumor Study (II)

Survival and cumulative frequency
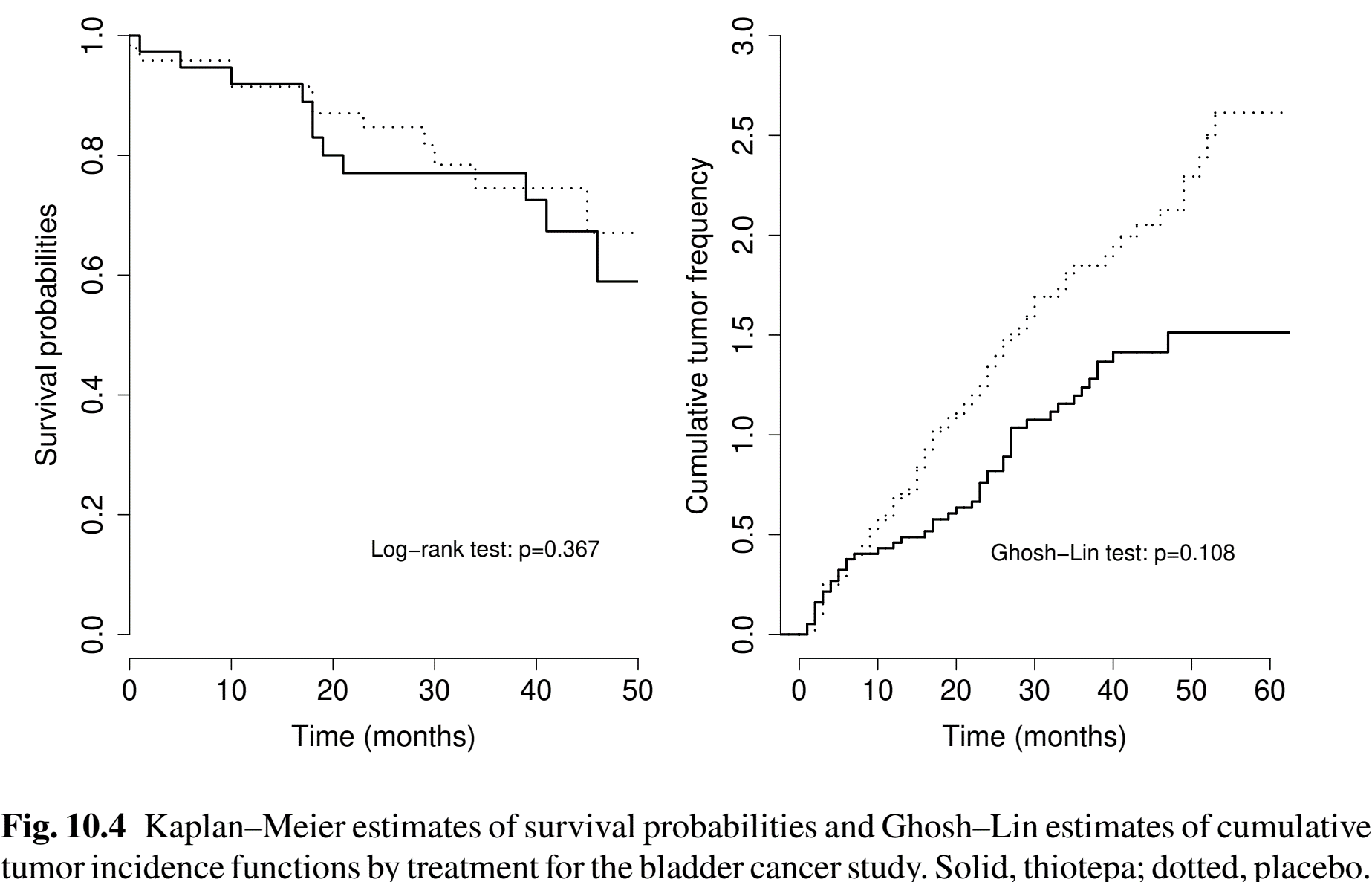
- Joint $\chi_2^2$ test: $p$-value 0.184

Conclusion

Notes

Fine–Gray regression
- Model diagnostics: R package crskdiag
- Proportional sub-distribution odds model (Eriksson et al., 2015)
```
library(timereg)
# Fit a proportional sub-distribution odds model for the kth risk
obj_po <- prop.odds.subdist(Event(time, status) ˜ covariates, cause = k)
```
- Interval-censored competing risks (Mao et al., 2018)
Semi-competing risks
- Term coined by Fine, Jiang, and Chappell (2001)
- Multivariate (here), multistate (Chapter 12), and composite (Chapter 13)
- Nonfatal event as mediator of treatment effect on death (Huang, 2021, 2022)

Summary

Competing risks
- Cause-specific hazard: conditional failure rate on survivors
  - coxph(Surv(time, status == k) ~ covariates)
- Cumulative incidence: marginal failure probability under other risks
  - Gray’s estimator/test cmprk::cuminc(ftime, fstatus, group, strata, rho = 0)
  - Fine-Gray model cmprk::crr(ftime, fstatus, cov1, failcode = k)
  - Tidy tables and graphics: tidycmprk package
Recurrent events in presence of death
- Ghosh-Lin methods
  - Nonparametric: rccf2::rccf(id, time, status, trt)
  - Proportional CF model: R packages mets and reReg

Applied Survival Analysis

Outline

Basic Quantities

Definition and Examples

Outcome Data & Identifiability

Two Approaches

Cause-Specific Hazard

Cumulative Incidence

CSH vs CIF

Comparison of Functions

Methods for Competing Risks

Observed Data

Cause-Specific Hazard Models (I)

Cause-Specific Hazard Models (II)

CIF: Nonparametric Estimation

CIF: Sub-Distribution Hazard

CIF: Gray’s Test

CIF: Fine-Gray Regression

Software: cmprsk::cuminc()

Software: cmprsk::crr() (I)

Software: cmprsk::crr() (II)

Software: tidycmprk Package (I)

Software: tidycmprk Package (II)

Bone Marrow Transplant Study

Study Information

Study Data

CIF by Donor Type (I)

CIF by Donor Type (II)

CIF by Donor Type (III)

Regression Analysis

Regression Results

Semi-Competing Risks

Definition and Examples

Data and Identifiability

Bivariate Analysis

Bivariate Analysis - GBC Example (I)

Bivariate Analysis - GBC Example (II)

Recurrent Events

Marginal Approaches

Software: rccf2::rccf()

Example: Bladder Tumor Study (I)

Example: Bladder Tumor Study (II)

Conclusion

Notes

Summary

Software: `cmprsk::cuminc()`

Software: `cmprsk::crr()` (I)

Software: `cmprsk::crr()` (II)

Software: `tidycmprk` Package (I)

Software: `tidycmprk` Package (II)

Software: `rccf2::rccf()`