Applied Survival Analysis

Chapter 4 - Cox Proportional Hazards Regression

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Model specification

  2. Partial-likelihood estimation and inference

  3. Residual analysis and goodness-of-fit

  4. Time-dependent covariates

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

The Cox Model

Regression Modeling

  • Regression vs testing
    • Multiple (quantitative) predictors
    • Quantify treatment effect
  • Cox proportional hazards (PH) model
    • Most popular for time-to-event data
    • Conditional (covariate-specific) hazard of \(T\) \[ \lambda(t\mid Z)\dd t = \pr(t\leq T < t +\dd t\mid T\geq t, Z) \]
      • \(Z=(Z_{\cdot 1},\ldots, Z_{\cdot p})^\T\): a \(p\)-vector of covariates
      • \(\lambda(t\mid z)\): risk for a subject in the sub-population with \(Z = z\)

Cox Proportional Hazards Model

  • Model specification \[\begin{equation}\label{eq:cox:model_spec} \lambda(t\mid Z)=\lambda_0(t)\exp(\beta^\T Z) \end{equation}\]
    • \(\beta=(\beta_1,\ldots,\beta_p)^\T\): \(p\)-dimensional regression coefficients
    • \(\lambda_0(t)\): (nonparametric) baseline hazard function
  • Proportionality: comparing two covariate groups \[\begin{equation}\label{eq:cox:prop_haz} \frac{\lambda(t\mid z_i)}{\lambda(t\mid z_j)}=\exp\{\beta^\T (z_i-z_j)\}. \end{equation}\]
    • \(\beta_k\): log-hazard ratio with one unit increase in \(Z_{\cdot k}\) \((k=1,\ldots, p)\)
      • one unit increase in \(Z_{\cdot k}\) increases (reduces) risk by \(\exp(\beta_k)\)

Parametric Sub-Model

  • Parametrize baseline function \[\begin{equation}\label{eq:cox:ph_param} \lambda(t\mid Z;\theta)=\lambda_0(t;\eta)\exp(\beta^\T Z) \end{equation}\]

    • \(\theta=(\beta, \eta)\)
  • Weibull PH model \[\begin{equation}\label{eq:cox:weibull_base} \lambda(t\mid Z;\theta)=\alpha\gamma^{-\alpha}t^{\alpha-1}\exp(\beta^\T Z). \end{equation}\]

  • Estimation

    • Maximum likelihood (Chapter 2)

Censored Data and Assumption

  • Observed data \[\begin{equation}\label{eq:cox:obs_data} (X_i, \delta_i, Z_i), \hspace{5mm} i=1,\ldots,n, \end{equation}\]
    • i.i.d. replicates of \((X, \delta, Z)\), where \(X=\min(T, C)\) and \(\delta=I(T\leq C)\)
  • Independent censoring (conditional) \[\begin{equation}\label{eq:cox:cond_ind} (C\indep T)\mid Z. \end{equation}\]
    • Censoring distribution can differ between covariate levels
    • Must be independent with outcome within each level

Parametric MLE

  • General form of score function (Chapter 2)
    • Martingale integral of hazard score \(\partial\log\lambda(t\mid Z,\theta)/\partial\theta\)
    • First component: \(\partial\log\lambda(t\mid Z,\theta)/\partial\beta=Z\)
  • Score function \[\begin{equation}\label{eq:cox:score} \Pn\left[\int_0^\infty\left\{Z_i^\T,\frac{\partial}{\partial\eta^\T}\log\lambda_0(t;\hat\eta)\right\}^\T\dd M_i(t;\hat\theta)\right]=0, \end{equation}\]
    • \(\dd M_i(t; \theta)=\dd N_i(t)-I(X_i\geq t)\exp(\beta^\T Z_i)\lambda_0(t;\eta)\dd t\)
    • Solve by standard Newton-Raphson algorithm

Semiparametric Model

  • Parametric constraints
    • Determine shape of baseline function

  • Semiparametric model

    • \(\beta\): parametric covariate effects
    • \(\lambda_0(\cdot)\): nonparametric time trend
    • Standard MLE does not apply due to nonparametric \(\lambda_0(\cdot)\)
  • Partial likelihood
    • Focus on data most relevant to covariate effects
    • A function of only \(\beta\) not \(\lambda_0(\cdot)\)

Partial Likelihood

Set-up

  • Observed event times \(t_1<\cdots<t_m\)
    • \(\mathcal F_j =\{(j)\}\): singleton index (assume no ties) for the subject that fails at \(t_j\)
    • \(\mathcal R_j\): set of indices for those at risk at \(t_j\)
    • Index \(i\) \(\to\) covariates \(Z_i\)

Conditional Information

  • Data most informative of \(\beta\)
    • Difference in risk between covariate groups
    • Identity of failed subject (\(\mathcal F_j\)) given a failure (\(d_j=1\)) among those at risk (\(\mathcal R_j\)) \[\begin{align}\label{eq:cox:cond_lik} \pr(\mathcal F_j\mid \mathcal R_j,d_j=1)&=\frac{\pr(\mbox{Subject $(j)$ fails given at risk at $t_j$})}{\pr(\mbox{One in $\mathcal R_j$ fails given all at risk at $t_j$})}\notag\\ &\approx\frac{\lambda(t_j\mid Z_{(j)})\dd t_j}{\sum_{i\in\mathcal R_j}\lambda(t_j\mid Z_i)\dd t_j}\notag\\ &=\frac{\exp(\beta^\T Z_{(j)})\lambda_0(t)\dd t_j}{\sum_{i\in\mathcal R_j}\exp(\beta^\T Z_i)\lambda_0(t)\dd t_j}\notag\\ &=\frac{\exp(\beta^\T Z_{(j)})}{\sum_{i\in\mathcal R_j}\exp(\beta^\T Z_i)} \end{align}\]
      • Indeed a function only of \(\beta\)

Partial Likelihood Construction

  • Combine over time

    • Partial likelihood \[\begin{align*} PL_n(\beta)=\prod_{j=1}^m\pr(\mathcal F_j\mid \mathcal R_j,d_j=1) =\prod_{j=1}^m\frac{\exp(\beta^\T Z_{(j)})}{\sum_{i\in\mathcal R_j}\exp(\beta^\T Z_i)} \end{align*}\]

    • Log-partial likelihood \[\begin{align}\label{eq:cox:pln} pl_n(\beta)=n^{-1}\log PL_n(\beta)&=n^{-1}\sum_{j=1}^m\left\{\beta^\T Z_{(j)}-\log\sum_{i\in\mathcal R_j}\exp(\beta^\T Z_i)\right\}\notag\\ &= n^{-1}\sum_{i=1}^n \delta_i\left\{\beta^\T Z_i- \log\sum_{j=1}^n I(X_j\geq X_i)\exp(\beta^\T Z_j) \right\}\notag\\ &=n^{-1}\sum_{i=1}^n\int_0^\infty \left\{\beta^\T Z_i- \log\sum_{j=1}^n I(X_j\geq t)\exp(\beta^\T Z_j) \right\}\dd N_i(t). \end{align}\]

Maximum Partial-Likelihood (MPLE)

  • Estimator: \(\hat\beta=\arg\max_\beta pl_n(\beta)\)
    • \(pl_n(\beta)\approx\) log-likelihood of a parametric model
    • Partial-likelihood score \[\begin{equation}\label{eq:cox:pl_score} U_n(\beta)=\frac{\partial}{\partial\beta} pl_n(\beta) =n^{-1}\sum_{i=1}^n\int_0^\infty \left\{Z_i- \frac{\sum_{j=1}^n I(X_j\geq t)Z_j\exp(\beta^\T Z_j)}{\sum_{j=1}^n I(X_j\geq t)\exp(\beta^\T Z_j)} \right\}\dd N_i(t) \end{equation}\]
      • Solve \(U_n(\hat\beta)=0\) (by Newton-Raphson)
    • Variance by inverse “information”
      • \(\hat\var(\hat\beta)=n^{-1}\hat{\mathcal I}^{-1}\)
      • \(\hat{\mathcal I}=-\partial U_n(\hat\beta)/\partial\beta\)

Martingale Framework

  • Equivalently \[\begin{equation}\label{eq:cox:pl_score_mart} U_n(\beta)=n^{-1}\sum_{i=1}^n\int_0^\infty \left\{Z_i- \frac{\sum_{j=1}^n I(X_j\geq t)Z_j\exp(\beta^\T Z_j)}{\sum_{j=1}^n I(X_j\geq t)\exp(\beta^\T Z_j)} \right\}\dd M_i(t;\beta,\Lambda_0), \end{equation}\]
    • \(\dd M_i(t;\beta,\Lambda_0)=\dd N_i(t)-I(X_i\geq t)\exp(\beta^\T Z_i)\dd \Lambda_0(t)\)
    • \(\var\{U_n(\beta)\}\) by variance formula for martingale integrals
    • Justifies \(\hat\var(\hat\beta)=n^{-1}\hat{\mathcal I}^{-1}\)

Inference on \(\beta\)

  • Individual hazard ratio: \(\exp(\beta_k)\) \((k=1,\ldots, p)\)
    • 95% CI \[\begin{equation}\label{eq:cox:hr_ci} \left[\exp\left\{\hat\beta_k-1.96\hat\se(\hat\beta_k)\right\}, \exp\left\{\hat\beta_k+1.96\hat\se(\hat\beta_k)\right\}\right] \end{equation}\]
  • Joint test of multiple coefficients
    • Multiple dummy variables of same categorical predictor (e.g., race groups) \[ H_0:\beta_{(q)}=(\beta_1,\ldots,\beta_q)^\T=0 \]
    • Wald test \[\begin{equation}\label{eq:cox:joint_test} \hat\beta_{(q)}^\T\hat\var(\hat\beta_{(q)})^{-1}\hat\beta_{(q)}\sim\chi_q^2 \end{equation}\]
      • \(\hat\var(\hat\beta_{(q)})\): sub-matrix of \(\hat\var(\hat\beta)\)

Breslow Estimator

  • Cumulative baseline function \(\Lambda_0(t)\)
    • By \(E\{\dd M_i(t;\beta,\Lambda_0)\}=0\): \[\begin{equation}\label{eq:cox:Lambda} \dd \Lambda_0(t)=\frac{E\{\dd N_i(t)\}}{E\{I(X_i\geq t)\exp(\beta^\T Z_i)\}}. \end{equation}\]
    • Breslow estimator \[\begin{equation}\label{eq:cox:breslow} \hat\Lambda_0(t)=\int_0^t\frac{\sum_{i=1}^n\dd N_i(s)}{\sum_{i=1}^n I(X_i\geq s)\exp(\hat\beta^\T Z_i)}. \end{equation}\]

Predicting Survival

  • Model-based survival function for given \(z\) \[ S(t\mid z;\beta,\Lambda_0)=\exp\left\{-\exp(\beta^\T z)\Lambda_0(t)\right\} \]
    • Plug in parameter estimates \[S(t\mid z;\hat\beta,\hat\Lambda_0)\]

Exercise: Conditional survival

A patient with covariate value \(z\) is censored at time \(c\). Use the fit model to predict his/her future survival probabilities.

Stratified Model

  • Stratification: within-stratum comparison
    • Sex, race, study center, etc.
    • Adjust for confounder without including it as covariate
      • No PH assumption across strata
  • Conditional hazard in \(l\)th stratum \[\begin{equation}\label{eq:cox:model_strat} \lambda_l(t\mid Z^{(l)})=\lambda_{0l}(t)\exp(\beta^\T Z^{(l)}) \end{equation}\]
    • \(\lambda_{0l}(\cdot)\): Stratum-specific baseline functions
      • Need not be proportional (useful in addressing non-proportionality in covariates)
    • \(\beta\): Common covariate effects
    • Estimation: Use sum of stratum-specific partial-likelihood scores

Software: survival::coxph() (I)

  • Basic syntax for Cox model
# Fit (time, status) vs covariates stratified by str_var
obj <- coxph(Surv(time, status) ~ covariates 
             + strata(str_var))
  • Input
    • Surv(time, status) ~ covariates: \((X, \delta) \sim Z\)
    • strata(str_var): stratified by variable str_var (optional)
  • Output: an object of class coxph
    • obj$coefficients: \(\hat\beta\)
    • obj$var: \(\hat\var(\hat\beta)\)

Software: survival::coxph() (II)

  • Breslow estimates \(\hat\Lambda_0(t)\)
# obj: coxph object
# centered = FALSE for baseline (Z = 0)
Lambda0 <- basehaz(obj, centered = FALSE)
  • Output: a data frame
    • Lambda0$time: \(t\); Lambda0$hazard: \(\hat\Lambda_0(t)\)
    • Lambda0$strata: levels of str_var if stratified by it
  • Prediction of survival
# Model-based survival estimates for new observations
survfit(obj, newdata)

Software: survival::coxph() (III)

  • Summary: summary(obj)
    • summary(obj)$coefficients: a matrix containing \(\hat\beta\), hazard ratio \(\exp(\hat\beta)\), \(\hat\se(\hat\beta)\), test statistic, and \(p\)-value as columns
  • Joint test of multiple coefficients
# Sample code for testing
# H_0: beta_1 = ... =  beta_q = 0
beta_q <- obj$coefficients[1:q] # get beta_(q)
Sigma_q <- obj$var[1:q, 1:q] # get q x q variance matrix
#chisq statistic with q d.f.
chi_q <- t(beta_q) %*% solve(Sigma_q) %*% beta_q
#p-value
pval <- 1 - pchisq(chi_q, q)

Software: gtsummary::tbl_regression()

  • Summary table

    • Specify label = list(...) for custom variable labels
    library(gtsummary)
# Fit (time, status) vs covariates stratified by str_var
obj <- coxph(Surv(time, status) ~ covariates)
# Summary table
tbl_regression(obj) # default: HR, 95% CI, p-value

Example: German Breast Cancer (I)

  • Endpoint: relapse-free survival

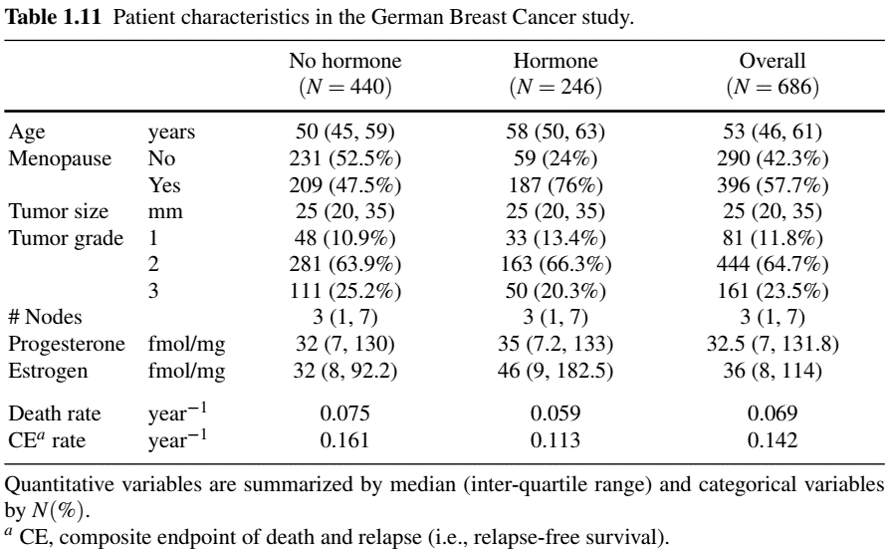
Example: German Breast Cancer (II)

  • Model fitting
#--- Data frame ---------------------
head(df)
#   id      time status hormone age meno size grade nodes prog estrg
# 1  1 43.836066      1       1  38    1   18     3     5  141   105
# 3  2 46.557377      1       1  52    1   20     1     1   78    14
# 5  3 41.934426      1       1  47    1   30     2     1  422    89
# 7  4  4.852459      0       1  40    1   24     1     3   25    11
# 8  5 61.081967      0       2  64    2   19     2     1   19     9
# 9  6 63.377049      0       2  49    2   56     1     3  356    64

#--- Model fitting ------------------
obj <- coxph(Surv(time, status)~ hormone + meno + age + size + grade
           + nodes + prog + estrg, data = df)

Example: German Breast Cancer (III)

  • Summary results

    • Hormone-treated women 70.7% times as likely to relapse/die as untreated
    #--- Summary results ------------------
summary(obj)
#>   n= 686, number of events= 299 
#>               coef exp(coef)  se(coef)      z Pr(>|z|)    
#> hormone2 -0.346278  0.707316  0.129075 -2.683 0.007301 ** 
#> meno2     0.258445  1.294915  0.183476  1.409 0.158954    
#> age      -0.009459  0.990585  0.009301 -1.017 0.309126    
#> size      0.007796  1.007827  0.003939  1.979 0.047794 *  
#> grade2    0.636112  1.889121  0.249202  2.553 0.010693 *  
#> grade3    0.779654  2.180718  0.268480  2.904 0.003685 ** 
#> nodes     0.048789  1.049998  0.007447  6.551  5.7e-11 ***
#> prog     -0.221724  0.801137  0.057353 -3.866 0.000111 ***
#> estrg     0.019731  1.019927  0.045037  0.438 0.661307    
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Example: German Breast Cancer (V)

  • Tumor grade?

    • Joint test on grade2 and grade3
    • \(\chi_2^2=9.4\), \(p=0.009\)
    #--- Wald test on tumor grade ------------------
# H_0: beta_5=beta_6=0
beta_q <- obj$coefficients[5:6]
Sigma_q <- obj$var[5:6,5:6]
#chisq statistic with 2 d.f.
chisq2 <- t(beta_q) %*% solve(Sigma_q) %*% beta_q
chisq2
# [1,] 8.440412
#p-value
pval <- 1 - pchisq(chisq2, 2)
pval
# [1,] 0.01469562

Example: German Breast Cancer (VI)

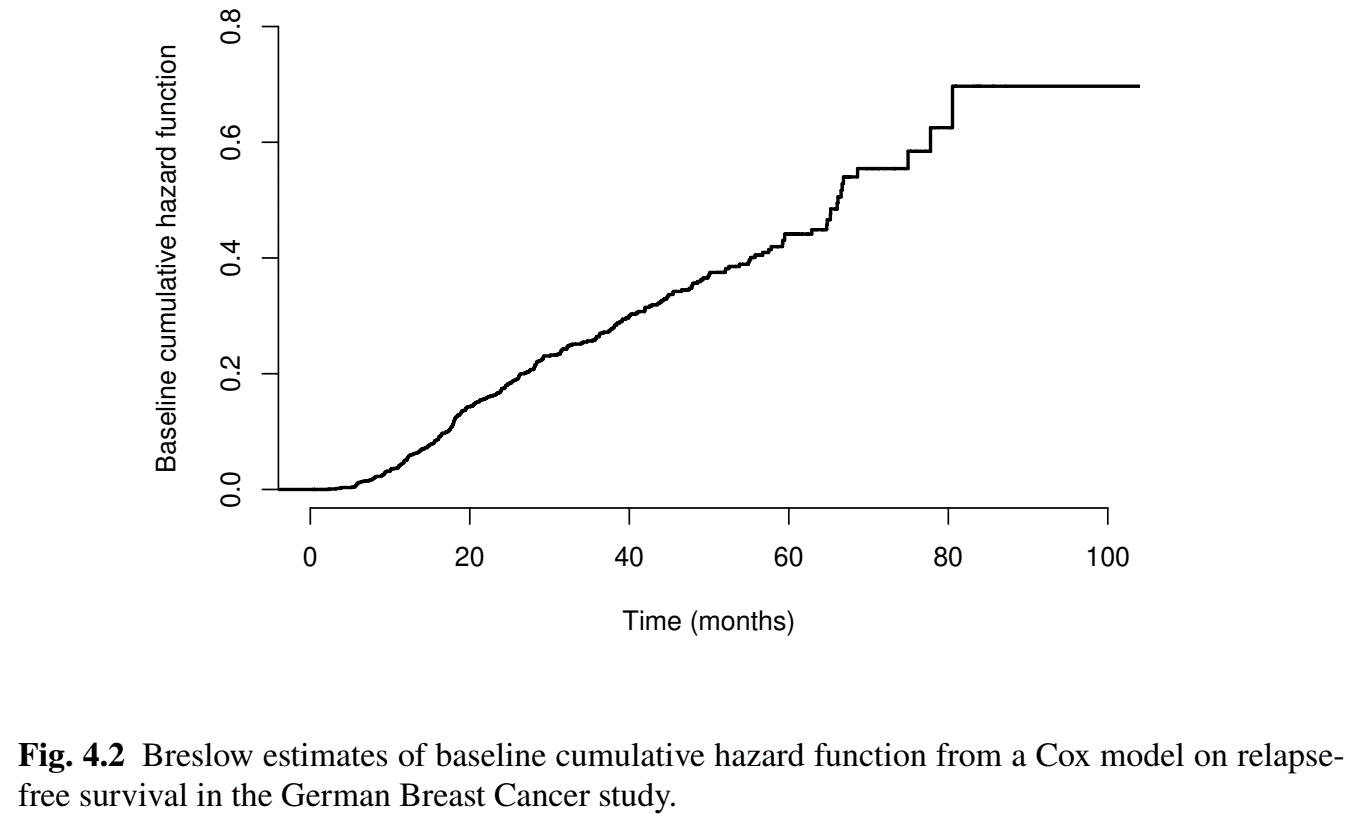
  • Baseline \(\hat\Lambda_0(t)\)
#--- Breslow estimates of baseline function ------------------
Lambda0 <- basehaz(obj, centered = FALSE)
# Plot the baseline hazard function
plot(stepfun(Lambda0$time, c(0, Lambda0$hazard)), do.points = FALSE, 
     cex.axis = 0.9, lwd = 2, frame.plot = FALSE, xlim = c(0, 100),
     ylim = c(0, 0.8), xlab = "Time (months)", 
     ylab = "Baseline cumulative hazard", main = "")

Exercise: Survival prediction

Predict survival function for arbitrary \(z\).

  • Use obj$coefficients (\(\hat\beta\)) and Lambda0 (\(\hat\Lambda_0(t)\))
  • Use survfit(obj, newdata)

Example: German Breast Cancer (VII)

  • Baseline \(\hat\Lambda_0(t)\)

Residual Analyses

Assumptions in Cox Model

  • Cox model assumptions \[\begin{equation} \lambda(t\mid Z)=\lambda_0(t)\exp(\beta^\T Z) \end{equation}\]
    • Proportionality (\(\beta\) is time-constant)
    • Functional form of \(Z_{\cdot k}\) (linear? quadratic? categorical?)
    • Link function \(\exp(\cdot)\) for \(\beta^\T Z\)
  • Residuals
    • Observed vs model-predicted
    • Model fits data \(\to\) predictions capture systematic trend \(\to\) random residuals
    • Pattern in residuals \(\to\) inadequate fit

Cox-Snell Residuals (I)

  • Standard result
    • \(S(T)\sim\mbox{Unif}[0, 1]\)
    • \(\Lambda(T)=-\log S(T) \sim \mbox{Expn}(1)\) (exponential with unit hazard rate)
  • Under Cox model \[ \Lambda(t\mid Z;\beta,\Lambda_0)=\exp(\beta^\T Z)\Lambda_0(t) \]
    • \(\Lambda(T\mid Z;\beta,\Lambda_0)\sim \mbox{Expn}(1)\)
    • \(\Lambda(X\mid Z;\beta,\Lambda_0)\): Censored version of \(\Lambda(T\mid Z;\beta,\Lambda_0)\sim \mbox{Expn}(1)\)
    • \(\{\hat s_i\equiv \Lambda(X_i\mid Z_i;\hat\beta,\hat\Lambda_0), \delta_i\}\): A sample of censored “times” from \(\mbox{Expn}(1)\)
      • \(\hat s_i\) \((i=1,\ldots, n)\): Cox-Snell residuals

Cox-Snell Residuals (II)

  • Nelsen-Aalen estimates \(\hat\Lambda_{\rm CS}(t)\)
    • Based on \((\hat s_i, \delta_i)\) \((i=1,\ldots, n)\)
    • Recovers cumulative hazard of \(\mbox{Expn}(1)\), i.e., \(\Lambda(t)=t\)
  • Graphical check
    • Overall fit: \(\hat\Lambda_{\rm CS}(\hat s_i)\approx \hat s_i\)
    • \(\log\hat\Lambda_{\rm CS}(\hat s_i)\) vs \(\log\hat s_i\): straight line passing through origin (similar to Q-Q plot)
    • Departure (e.g., curvature) suggests lack of fit
      • Doesn’t tell which assumptions are violated

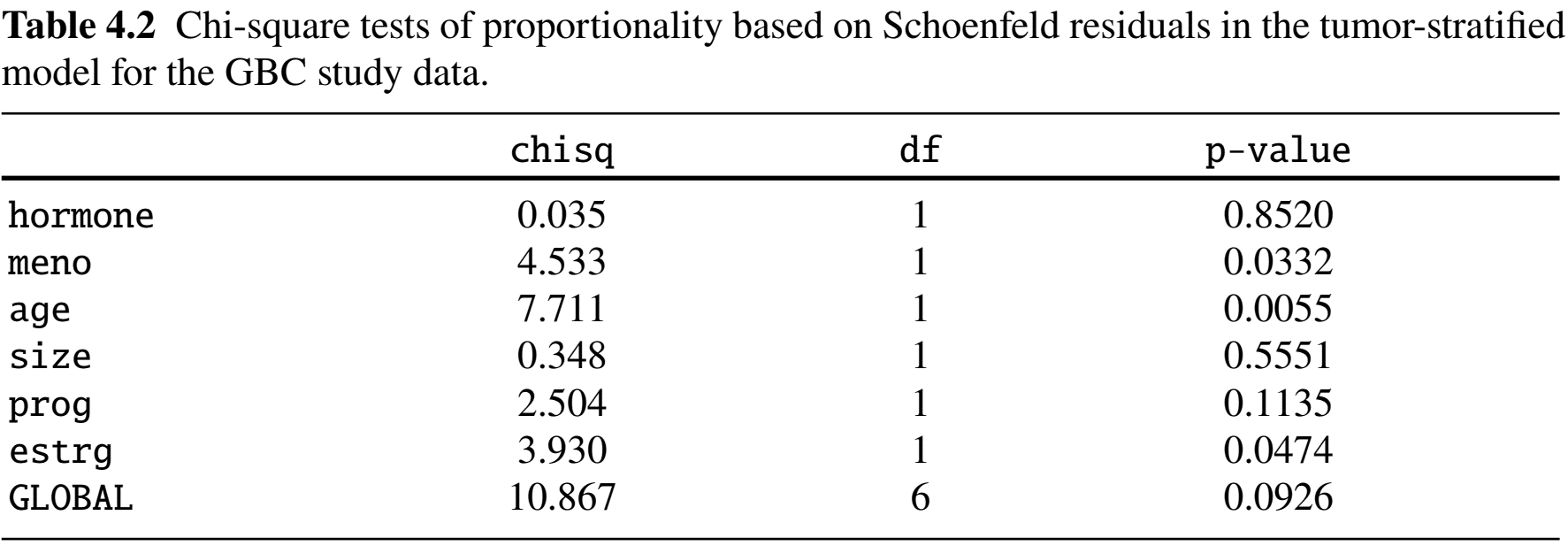
Schoenfeld Residuals (I)

  • Defined only for failed subjects \[\begin{equation}\label{eq:cox:schoenfeld} \hat r_i=Z_i-\mathcal E(X_i;\hat\beta) \hspace{10mm} (\delta_i=1; i=1,\ldots,n). \end{equation}\]
    • \(\mathcal E(t_j;\beta) = E(Z_{(j)}\mid \mathcal R_j, d_j=1)=\frac{\sum_{j=1}^nI(X_j\geq t)Z_j\exp(\beta^\T Z_j)}{\sum_{j=1}^nI(X_j\geq t)\exp(\beta^\T Z_j)}\)
    • Observed minus (conditionally) expected covariates
    • Sensitive to proportionality (canceling of \(\lambda_0(\cdot)\))
    • \(\hat r_{ik}\) (rescaled) vs \(X_i\): mean zero if proportionality holds on \(Z_{\cdot k}\)
    • Formal \(\chi^2\) tests based on the \(\hat r_{ik}\) (with proportionality as \(H_0\))
      • Serve only as guidelines to graphical results

Schoenfeld Residuals (II)

  • In case of non-proportionality
    • HR changes over time
    • Stratify rather than set as covariate
    • Include covariate \(\times\) time interaction, e.g., \(Z_{\cdot k}\log(t)\)
    • Choose alternatives over Cox model (Chapter 5)
      • Restricted mean life
      • Additive hazards
      • Proportional odds
      • Accelerate failure time (AFT)

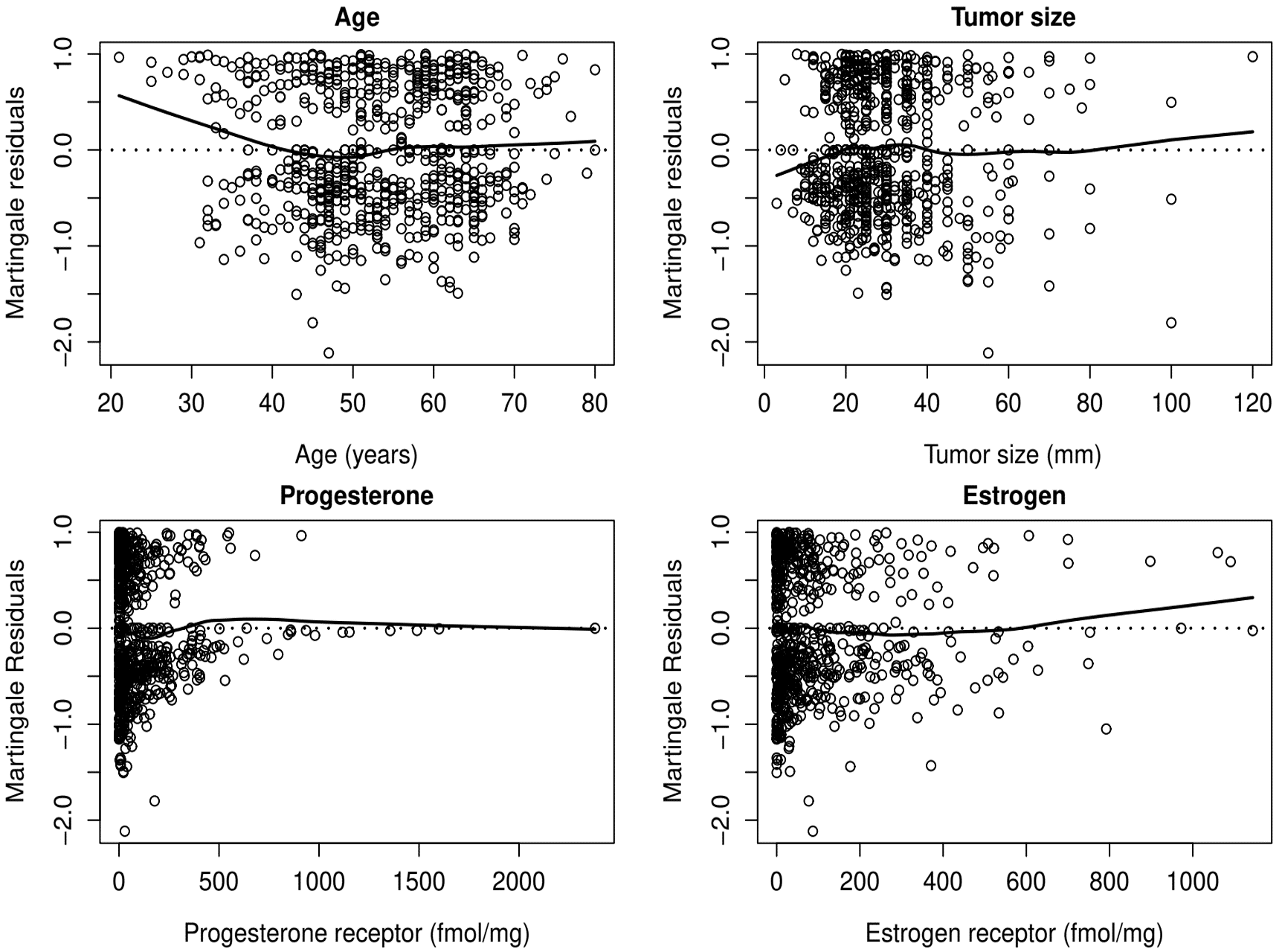
Martingale/Deviance Residuals

  • Usual residuals: observed response minus expected \[\begin{align*} M_i(X_i; \hat\beta,\hat\Lambda_0)&=N_i(X_i)-\int_0^{X_i} I(X_i\geq t)\exp(\hat\beta^\T Z_i)\dd \hat\Lambda_0(t)\\ &=\delta_i-\exp(\hat\beta^\T Z_i)\hat\Lambda_0(X_i) \end{align*}\]
    • \(\exp(\hat\beta^\T Z_i)\hat\Lambda_0(X_i)\) is Cox-Snell residual
    • Functional form of \(Z_{\cdot k}\): plot \(M_i(X_i; \hat\beta,\hat\Lambda_0)\) against \(Z_{ik}\) \((i=1,\ldots, n)\)
      • Inappropriate form \(\to\) transform by log, square root, power, or grouping
    • Link function: plot \(M_i(X_i; \hat\beta,\hat\Lambda_0)\) against \(\hat\beta^\T Z_i\)
    • Deviance residuals: Standardized/symmetrized martingale residuals \(\to\) outlier detection

Software: survival::resid() (I)

  • Basic syntax for Cox model residuals
# obj: object returned by coxph()
resid(obj, type = c("martingale", "deviance", "score", "schoenfeld", 
                    "dfbeta", "dfbetas", "scaledsch", "partial"))
  • Cox-Snell residuals
# Calculate Cox-Snell by martingale residuals 
# df: data frame
coxsnellres <- df$status - resid(obj, type = "martingale")
# Compute Nelsen-Aalen estimates for cumulative hazard
fit <- survfit(Surv(coxsnellres, df$status) ~ 1)
Lambda <- cumsum(fit$n.event / fit$n.risk)
# Scatter plot
plot(log(fit$time), log(Lambda), xlab = "log(t)", 
     ylab = "log-cumulative hazard")
abline(0, 1, lty = 3) # add a dotted reference line

Software: survival::cox.zph()

  • Rescaled Schoenfeld residuals
# rescaled Schoenfeld residuals and tests
sch <- cox.zph(obj)
  • Output
    • sch$table: \(\chi^2\) tests of proportionality (each covariate and overall)
    • sch$time: \(m\)-vector of the \(X_i\)
    • sch$y: \((m\times p)\)-matrix of the rescaled \(\hat r_i\)
    • plot(sch): plot the residuals, one covariate per panel

Software: survival::resid() (II)

  • Martingale/Deviance residuals

    • df: data frame
    • zk: name of covariate of interest
    # Get the residuals
mart_resid <- resid(obj, type = 'martingale') # n-vector of martingale
dev_resid <- resid(obj, type = 'deviance') # n-vector of deviance
# Scatter plot residuals against covariate
plot(df$zk, mart_resid)
lines(lowess(df$zk, mart_resid)) # add a smooth line through points
abline(0, 0, lty = 3) # add a dotted reference line

Example: German Breast Cancer (VIII)

  • Overall fit - Cox-Snell residuals
# Compute the residuals
coxsnellres <- df$status-resid(obj, type="martingale")
## Then use N-A method to estimate the cumulative 
## hazard function for residuals
fit <- survfit(Surv(coxsnellres,df$status) ~ 1)
Htilde <- cumsum(fit$n.event/fit$n.risk)
# Scatter plot
plot(log(fit$time), log(Htilde), xlab="log(t)", frame.plot = FALSE,
     ylab="log-cumulative hazard", xlim = c(-8, 2), ylim = c(-8, 2))
abline(0, 1, lty = 3, lwd = 1.5) # add a reference line

Example: German Breast Cancer (IX)

  • Overall fit - Cox-Snell residuals

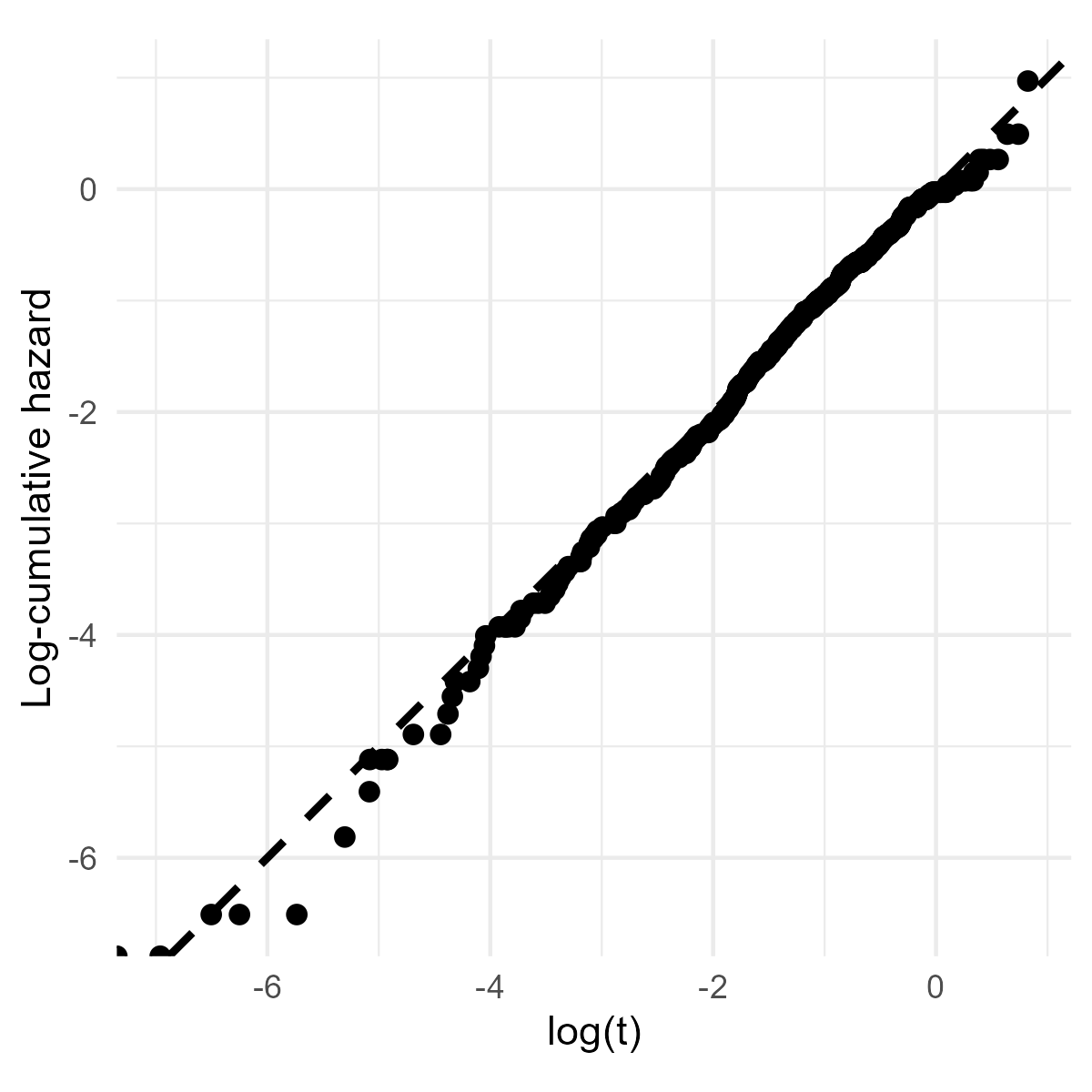
Example: German Breast Cancer (X)

  • Proportionality - Schoenfeld residuals
# Rescaled Schoelfeld residuals
sch <- cox.zph(obj) 
sch$table # chi-square tests

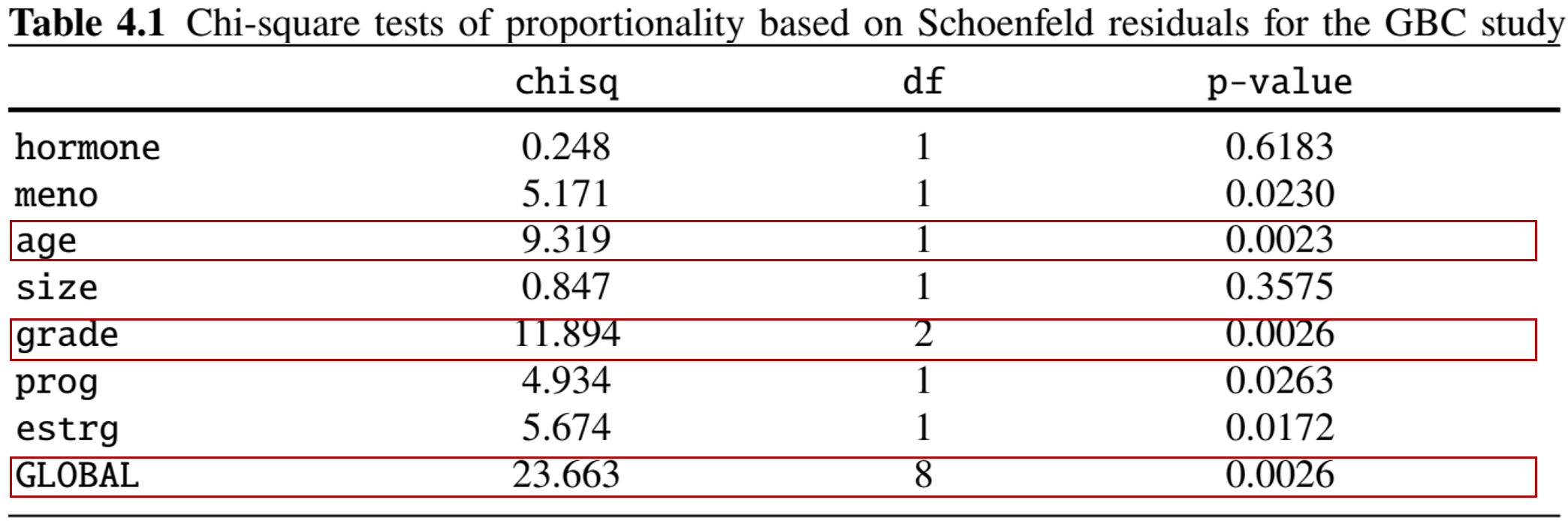
Example: German Breast Cancer (XI)

  • Proportionality - Schoenfeld residuals
# Plot rescaled Schoenfeld residuals for each covariate directly
plot(sch, xlab="Time (months)", lwd=2, cex.lab=1.2, cex.axis=1.2,
     ylab = c("Hormone", "Menopause", "Age", "Tumor size",
               "Tumor grade", "Progesterone", "Estrogen"))

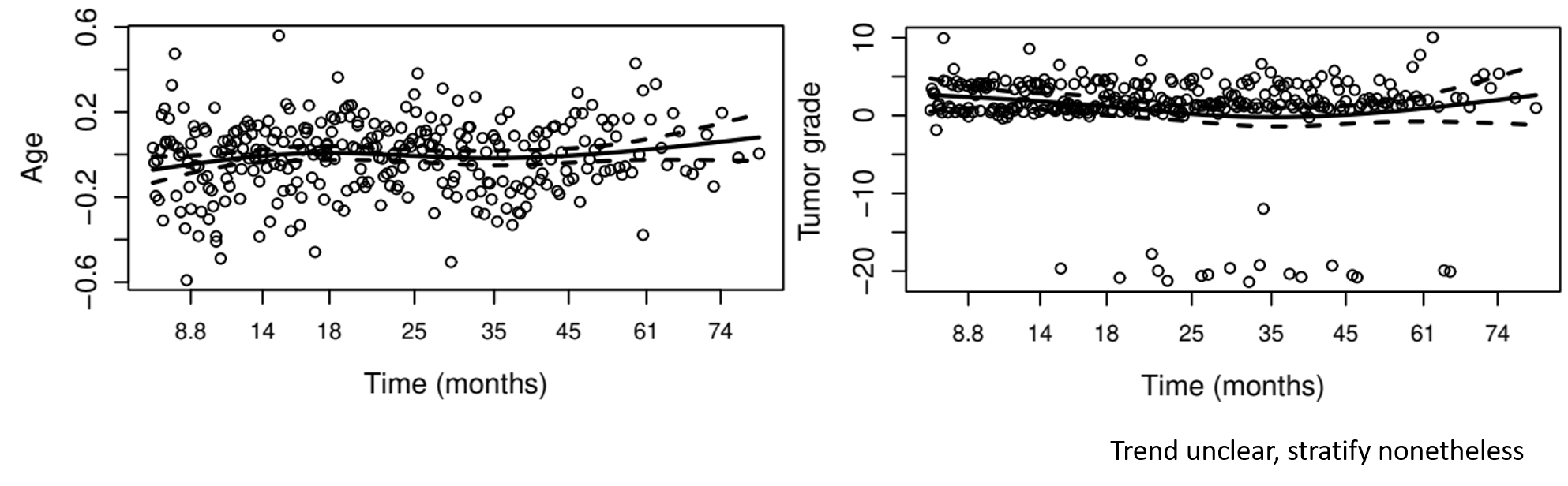
Example: German Breast Cancer (XII)

  • Stratification by tumor grade
# fit a Cox model stratified by tumor grade
obj_stra <- coxph(Surv(time, status) ~ hormone + meno
         + age + size + prog + estrg + strata(grade), data = df)
cox.zph(obj_stra)$table # proportionality tests

Example: German Breast Cancer (XIII)

  • Covariate form - Martingale (deviance) residuals
## Martingale residuals
mart_resid <- resid(obj_stra,type = 'martingale')
#plot residuals against, e.g., age
plot(df$age, mart_resid, main='Age', cex.lab=1.2, cex.axis=1.2,
     xlab="Age (years)", ylab="Martingale residuals")
lines(lowess(df$age, mart_resid), lwd = 2) # add a smooth line
abline(0, 0, lty = 3, lwd = 2) # add a reference line

Example: German Breast Cancer (XIV)

  • Covariate form - Martingale (deviance) residuals

Example: German Breast Cancer (XV)

  • Covariate form - Martingale (deviance) residuals

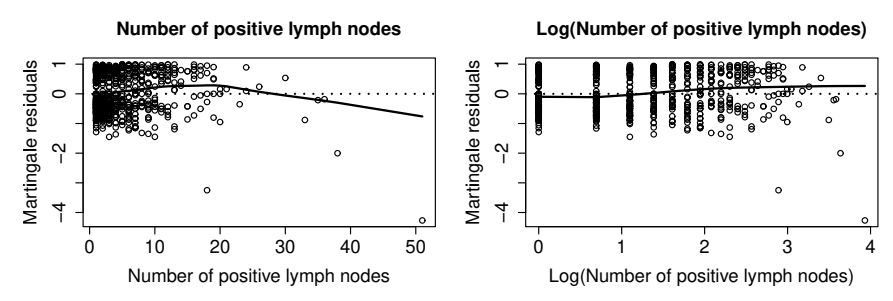
Example: German Breast Cancer (XVI)

  • Transformations
    • Categorize age: agec=1: \(\leq 40\) yrs; agec=2: \((40, 60]\) yrs; agec=3: \(> 60\) yrs
    • Log-transform nodes: log_nodes = log(nodes)
# Call:
# coxph(formula = Surv(time, status) ~ hormone + meno + agec + 
#     size + log_nodes+ prog + estrg + strata(grade), data = df)
#                coef exp(coef)  se(coef)      z Pr(>|z|)    
# hormone2  -0.402106  0.668910  0.128995 -3.117  0.00183 ** 
# meno2      0.247223  1.280465  0.156266  1.582  0.11363    
# agec2     -0.499979  0.606544  0.197677 -2.529  0.01143 *  
# agec3     -0.497538  0.608026  0.249509 -1.994  0.04614 *  
# size       0.006665  1.006688  0.003956  1.685  0.09205 .  
# log_nodes  0.477734  1.612417  0.066199  7.217 5.33e-13 ***
# prog      -0.229536  0.794902  0.057190 -4.014 5.98e-05 ***
# estrg      0.030350  1.030816  0.046469  0.653  0.51367

Example: German Breast Cancer (XVII)

  • Categorize age
    • Age differences masked by inappropriate linear form (\(p\)-value 0.309)

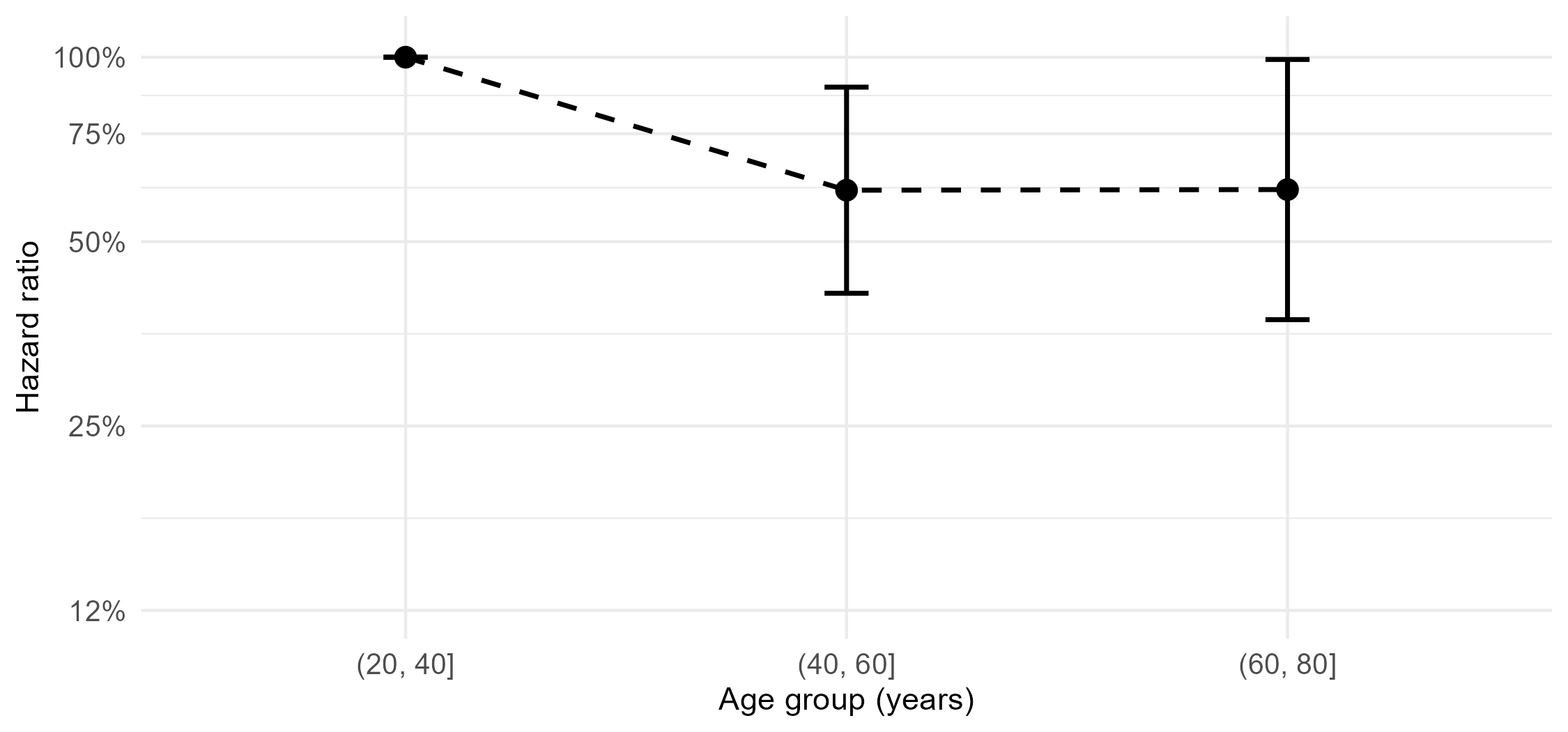
Example: German Breast Cancer (XVIII)

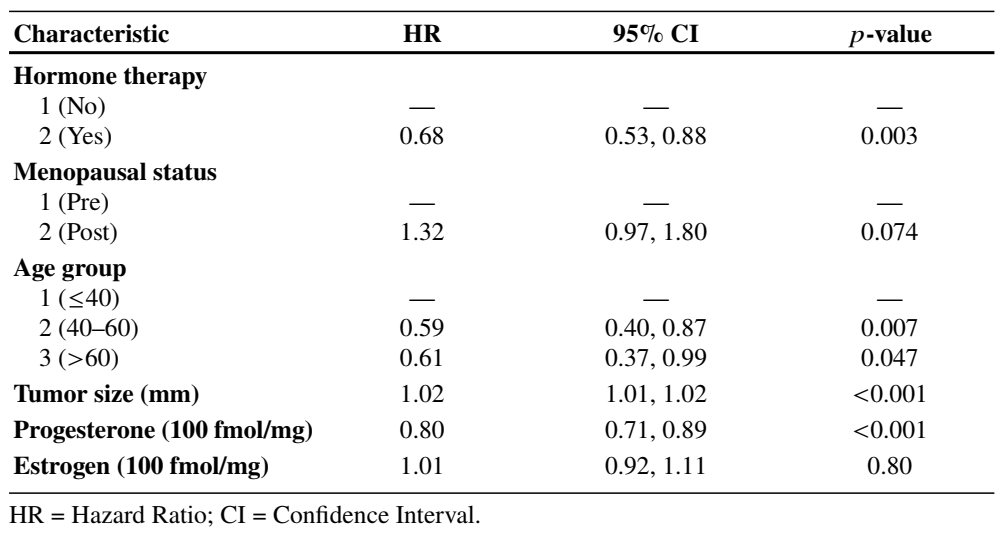
  • Tabulate final model
# Tabulate final model results
tbl_final <- tbl_regression(
  obj_stra_final, 
  exponentiate = TRUE,
  label = list(
    hormone = "Hormone", 
    meno    = "Menopause",
    agec    = "Age group",
    size    = "Tumor size (mm)",
    log_nodes   = "Log-number of positive lymph nodes",
    prog    = "Progesterone (100 fmol/mg)",
    estrg   = "Estrogen  (100 fmol/mg)"
  )
)

Example: German Breast Cancer (XIX)

  • Final model

Time-Dependent Covariates

Internal vs External Covariates

  • Notation: \(Z(t)=\{Z_{\cdot 1}(t),\ldots, Z_{\cdot p}(t)\}^\T\)
  • Internal covariates
    • Measured on same subject during follow-up, influenced by failure process
      • Biomarkers (CD4 cell count), quality of life, other events
    • Modeling: current (instantaneous) risk vs covariate history
  • External covariates
    • Extraneous factors, changes unaffected by subject’s failure process
      • Pre-planned treatment sequence, environmental factors, baseline covariates \(\times\) time
    • Modeling: risk profile vs entire covariate path

Internal Covariates

  • Modeling target (intensity function) \[ \lambda\{t\mid\overline Z(t)\}\dd t=\pr\{t\leq T<t+\dd t\mid T\geq t, \overline Z(t)\} \]
    • \(\overline Z(t)=\{Z(u): 0\leq u\leq t\}\): covariate path up to \(t\)
  • Model specification \[\begin{equation}\label{eq:cox:time_varying_model} \lambda\{t\mid\overline Z(t)\}=\lambda_0(t)\exp\{\beta^\T Z(t)\}. \end{equation}\]
    • Current risk depends on past only through \(Z(t)\)
    • Define \(Z(t)\) to be useful summary of past
      • should not be “current” measurements due to delay in cause and effect
    • Example: frequency of drug use in past week, month, or year

External Covariates (I)

  • Modeling target (hazard function) \[ \lambda(t\mid Z)\dd t=\pr(t\leq T<t+\dd t\mid T\geq t, Z) \]
    • \(Z=\{Z(t):0\leq t\leq \infty\}\): entire covariate path
  • Model specification \[\begin{equation}\label{eq:cox:time_varying_model_ex} \lambda(t\mid Z)=\lambda_0(t)\exp\{\beta^\T Z(t)\}. \end{equation}\]
    • \(Z(t)\): useful summary before \(t\)
    • Conditional survival (not applicable to internal covariates) \[ S(t\mid Z)=\exp\left\{-\int_0^t\lambda(s\mid Z)\dd s\right\}=\exp\left[-\int_0^t\exp\{\beta^\T Z(s)\}\lambda_0(s)\dd s\right] \]

External Covariates (II)

  • Baseline covariates \(times\) time
    • Addressing non-proportionality
  • Example: \(Z_{\cdot 1} = 1, 0\)
    • Non-proportionality: \(\lambda(t\mid Z_{\cdot 1} =1)/\lambda(t\mid Z_{\cdot 1} =0)\) changes with \(t\)
    • Add \(Z_{\cdot 2}(t) = Z_{\cdot 1} t\), then \[\lambda(t\mid Z_{\cdot 1}, Z_{\cdot 2})=\exp\{\beta_1Z_{\cdot 1} + \beta_2Z_{\cdot 2}(t)\}\lambda_0(t)\] So \[ \frac{\lambda(t\mid Z_{\cdot 1}=1)}{\lambda(t\mid Z_{\cdot 1}=0)}=\exp(\beta_1+\beta_2 t) \]
    • Hopefully captures temporal pattern of effect size

Estimation and Inference

  • Same inference procedure: partial likelihood \[\begin{align*} PL_n(\beta)=\prod_{j=1}^m\frac{\exp\{\beta^\T Z_{(j)}(t_j)\}}{\sum_{i\in\mathcal R_j}\exp\{\beta^\T Z_i(t_j)\}}. \end{align*}\]
  • Partial-likelihood score \[ U_n(\beta)=n^{-1}\sum_{i=1}^n\int_0^\infty \left\{Z_i(t)- \frac{\sum_{j=1}^n I(X_j\geq t)Z_j(t)\exp\{\beta^\T Z_j(t)\}}{\sum_{j=1}^n I(X_j\geq t)\exp\{\beta^\T Z_j(t)\}} \right\}\dd N_i(t) \]
    • Same Newton-Raphson algorithm

Software: survival::coxph() (IV)

  • Basic syntax for time-varying covariates
# (start, stop): left and right ends of time period
# event: 1 = event; 0 = no event
obj <- coxph(Surv(start, stop, event) ~ covariates)
  • Input
    • Data in counting process (long) format (multiple records per subject)
    • (start, stop): period during which covariate takes on a particular value
    • event: event indicator at time stop
      • event = 0 need not mean censoring (why?)
  • Output: coxph object

Software: survival::coxph() (V)

  • Residual analysis

    • Subject indexing to aggregate residuals
    # Residual calculations for Cox model with time-varying covariates
residuals(obj, type = c("martingale", "deviance", "schoenfeld", "score",
                        "scaledsch", "dfbeta", "dfbetas", "partial"),
               collapse = df$id # specify subject ID
            )

Example: Stanford Heart Study (I)

  • Heart transplant study (1967–74)
    • Population: 103 cardiac patients in transplantation program
    • Objective: Evaluate effect of transplant (time-varying) on time from enrollment to death

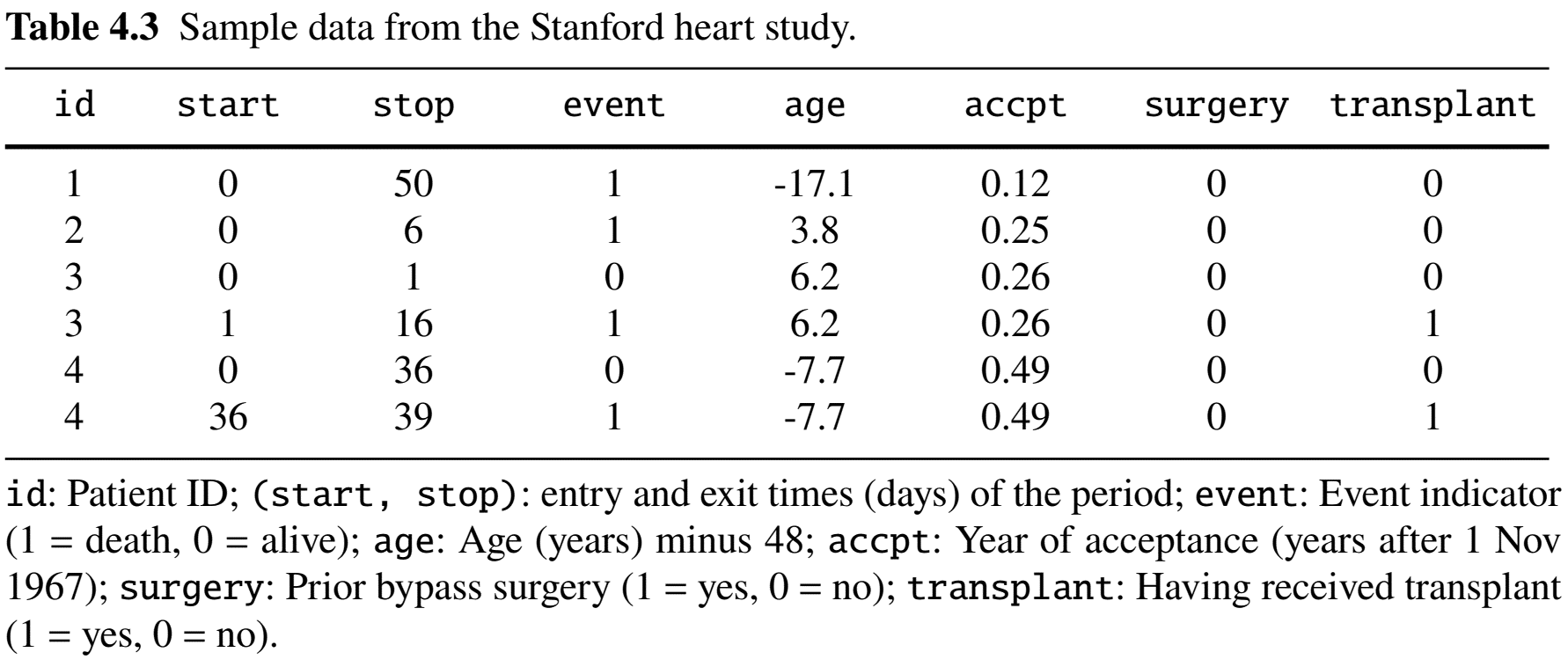
Example: Stanford Heart Study (II)

  • Results
    • Adjusting for other predictors, receiving a transplant reduces the risk of mortality by \(1-0.990=1.0\%\) (\(p\)-value 0.974)
# Call:
# coxph(formula = Surv(start, stop, event) ~ age + accpt + surgery + 
#       transplant, data = heart)
# 
#   n= 172, number of events= 75 
# 
#                 coef exp(coef) se(coef)      z Pr(>|z|)  
# age          0.02717   1.02754  0.01371  1.981   0.0476 *
# accpt       -0.14635   0.86386  0.07047 -2.077   0.0378 *
# surgery     -0.63721   0.52877  0.36723 -1.735   0.0827 .
# transplant1 -0.01025   0.98980  0.31375 -0.033   0.9739  
---

Example: Stanford Heart Study (III)

  • Internal or external
    • External: if donor matching follows predetermined protocol
    • Internal: if donor matching depends on patient’s health status
      • Critically ill more likely to receive transplant sooner
  • Model diagnostics
    • Exercise

Conclusion

Notes (I)

  • Partial likelihood
    • Original introduced by Sir David R. Cox (Cox, 1972)
    • Statistically efficient (\(\S\) 5.2 of Tsiatis, 2006)
    • Widely used by statisticians and medical researchers alike
  • Residual analysis
    • Cox–Snell residuals by Kay (1977)
    • Schoenfeld residuals by Schoenfeld (1980, 1982)
    • Proportionality tests implemented in cox.zph() based on Grambsch and Therneau (1994)

Notes (II)

  • Time-varying coefficients

    • Hazard raio changing over time \[ \lambda\bigl(t \mid Z\bigr) = \lambda_0(t) \exp\bigl\{\beta(t)^\T Z\bigr\} \]
    • Covariate \(\times\) time
    # Fit a Cox model with time-varying hormone treatment effect
obj_horm_tv <- coxph(
  Surv(time, status) ~ hormone + tt(hormone) + meno + agec + size
                 + log_nodes + prog + estrg + strata(grade),
  data = df,
  # Define time transformation: x * t (linear time interaction)
  tt = function(x, t, ...) x * t
)

Notes (III)

  • Spline models

    • Flexible forms for continuous covariates
    # Fit a Cox model with penalized splines for age
cox_spline <- coxph(Surv(time, status) ~ pspline(age, df = 4) + hormone 
                + meno + size + grade + prog + estrg, data = df)

Summary (I)

  • Cox proportional hazards (PH) model \[\begin{equation} \lambda(t\mid Z)=\lambda_0(t)\exp(\beta^\T Z) \end{equation}\]
    • \(\exp(\beta)\): hazard ratios associated with unit increases in \(Z\)
    • \(\hat\beta\): partial-likelihood estimator
    • \(\hat\Lambda_0(t)\): Breslow estimator
    • Stratification: adjustment without proportionality constraint
    • Survival prediction: \(S(t\mid z;\hat\beta,\hat\Lambda_0)\)
    • R-function: survival::coxph()
    • SAS procedure: PHREG

Summary (II)

  • Residual analysis
    • Cox-Snell: Overall fit
      • df$status - residuals(obj, type = "martingale")
    • Schoenfeld: Proportionality
      • cox.zph(obj)
    • Martingale/Deviance: Covariate form, link function, outlier
      • residuals(obj, type = c("martingale", "deviance"))
  • Time-varying covariates
    • Internal vs external
    • coxph(Surv(start, stop, event) ~ covariates)

HW3 (Due Mar 4)

  • Problem 4.8
  • Problem 4.15
  • Problems 4.17 and 4.23
  • Extra credit: Problem 4.24