Statistical Methods for Composite Endpoints: Win Ratio and Beyond

Chapter 4 - Semiparametric Regression

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

April 25, 2025

Outline

  • Proportional win-fractions (PW) model

    • Model specification
      • An extension of Cox PH model and two-sample WR
    • Estimation and residual analysis
    • HF-ACTION example (WR package)

  • High-dimensional data

    • Regularization by elastic net
    • HF-ACTION example (WRNet package)

\[\newcommand{\d}{{\rm d}} \newcommand{\T}{{\rm T}} \newcommand{\dd}{{\rm d}} \newcommand{\cc}{{\rm c}} \newcommand{\pr}{{\rm pr}} \newcommand{\var}{{\rm var}} \newcommand{\se}{{\rm se}} \newcommand{\indep}{\perp \!\!\! \perp} \newcommand{\Pn}{n^{-1}\sum_{i=1}^n} \newcommand\mymathop[1]{\mathop{\operatorname{#1}}} \newcommand{\Ut}{{n \choose 2}^{-1}\sum_{i<j}\sum} \def\a{{(a)}} \def\b{{(1-a)}} \def\t{{(1)}} \def\c{{(0)}} \def\d{{\rm d}} \def\T{{\rm T}} \def\bs{\boldsymbol} \def\C{{\mathcal C}} \def\S{{\mathcal S}} \def\Sk{{\mathcal S}^{(k)}} \newcommand{\wh}{\widehat} \]

Regression Framework

  • Regression vs two-sample
    • Adjustment for confounding
    • Quantitative predictors
    • Statistical efficiency
    • Screening of prognostic factors
      • Treatment, demographics (e.g., age, race, sex), medical history (e.g., diabetes, prior CVD), current medication (e.g., \(\beta\)-blocker, ACE inhibitor)
Univariate Hierarchical composite
Hypothesis testing Gehan, log-rank Win ratio/odds, net benefit (Ch 2)
Nonparametric estimation RMST RMT-IF (Ch 3)
Semiparametric regression Cox PH model ?

PW Model

Win Ratio Regression

  • Modeling target
    • Two independent subjects \((\mathcal H^*_i, Z_i)\) and \((\mathcal H^*_j, Z_j)\)
      • \(E\{\mathcal W(\mathcal H^*_i,\mathcal H^*_j)(t)\mid Z_i, Z_j\}\): Conditional win fraction (probability) for \(i\) against \(j\) at \(t\)
      • \(E\{\mathcal W(\mathcal H^*_j,\mathcal H^*_i)(t)\mid Z_i, Z_j\}\): Conditional win fraction (probability) for \(j\) against \(i\) at \(t\)
    • Covariate-specific win ratio \[\begin{equation}\label{eq:cov_spec_curtail_wr} WR(t; Z_i, Z_j;\mathcal W):= \frac{E\{\mathcal W(\mathcal H^*_i,\mathcal H^*_j)(t)\mid Z_i,Z_j\}}{E\{\mathcal W(\mathcal H^*_j,\mathcal H^*_i)(t)\mid Z_i, Z_j\}} \end{equation}\]
    • Regress \(WR(t; Z_i, Z_j;\mathcal W)\) vs \((Z_i, Z_j)\)
      • \(WR(t; Z_i, Z_j;\mathcal W) \geq 0\)
      • \(WR(t; Z_i, Z_j;\mathcal W) = WR(t; Z_j, Z_i;\mathcal W)^{-1}\)

Model Specification

  • Proportional win-fractions (PW) model

    • Multiplicative effects (Mao & Wang, 2021) \[\begin{equation}\label{eq:wr_reg} WR(t\mid Z_i, Z_j;\mathcal W)=\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\} \end{equation}\]

    • PW: covariate-specific win/loss fractions proportional over time

      • WR constant over time

    • \(\beta\): log-WR associated with unit increases in covariates (regardless of follow-up time)

    • Semiparametric: Parametric covariate effects, nonparametric otherwise

    • Denote model by PW(\(\mathcal W\))

      • Stresses dependency on win function

Special Cases

  • Two-sample WR
    • \(\exp(\beta)\): WR comparing group \(Z=1\) with group \(Z=0\)
  • Cox PH model
    • PW\((\mathcal W_{\rm TFE})\) \(\Leftrightarrow\) Cox PH model on TFE \(\tilde T\) \[ \pr(t\leq \tilde T<t+\dd t\mid \tilde T\geq t; Z) =\exp(-\beta^\T Z)\lambda_0(t)\dd t \]
  • Bivariate Lehmann model
    • PW\((\mathcal W_{\rm P})\) \(\Leftarrow\) Lehmann model on \((D, T_1)\) \[ \pr(D>s, T_1 > t\mid Z) = H_0(s, t)^{\exp(-\beta^\T Z)} \]
      • PH on both \(D\) and \(\{T_1\mid D\}\) with same HRs \(\exp(-\beta)\)

Censored Data and Win Residual

  • Observed outcomes
    • \(\mathcal H^*(X_i)\): outcomes up to \(X_i=D_i\wedge C_i\)
    • Observed win process \(\delta_{ij}(t)=\mathcal W(\mathcal H^*_i,\mathcal H^*_j)(X_i\wedge X_j\wedge t)\)
    • Determinacy (win or loss) indicator: \(R_{ij}(t)=\delta_{ij}(t)+\delta_{ji}(t)\)
  • Win residuals
    • Definition \[\begin{equation}\label{eq:wr:resid} M_{ij}(t\mid Z_i, Z_j;\beta)=\underbrace{\delta_{ij}(t)}_{\rm observed\,\,win} - \underbrace{R_{ij}(t)\frac{\exp\left\{\beta^{\rm T}\left( Z_i- Z_j\right)\right\}}{ 1+\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\}}}_{\rm model-based\,\, prediction} \end{equation}\]
    • \(E\{M_{ij}(t\mid Z_i, Z_j;\beta)\mid Z_i, Z_j\} =0\) for all \(t\)

Estimation and Inference

  • Estimating equation
    • Sum of all possible pairs of covariate-/time-weighted residuals \[\begin{equation}\label{eq:wr:ee} \Ut\int_0^\infty (Z_i - Z_j) h(t; Z_i, Z_j)\dd M_{ij}(t \mid Z_i, Z_j;\beta)=0 \end{equation}\]
    • Weight function \(h(t; Z_i, Z_j)\equiv 1\)
    • Newton-Raphson to get root \(\hat\beta\)
    • \(\hat\var(\hat\beta)\): \(U\)-statistic variance

Checking Proportionality

  • Cumulative residuals
    • Rescaled \(\hat U_n(t)=\Ut(Z_i - Z_j)M_{ij}(t \mid Z_i, Z_j;\hat\beta)\)
    • Similar to score processes in Cox model (Lin et al., 1993)

Stratified Model

  • Address non-proportionality
    • Categorical predictor \(\to\) stratifier
  • Stratified PW model
    • Idea: within-stratum comparisons (Dong et al., 2017, 2023)
    • Model specification (Wang & Mao, 2022) \[ \frac{E\{\mathcal W(\mathcal H^*_{li},\mathcal H^*_{lj})(t)\mid Z_{li},Z_{lj}\}}{E\{\mathcal W(\mathcal H^*_{lj},\mathcal H^*_{li})(t)\mid Z_{li}, Z_{lj}\}} = \exp\left\{\beta^{\rm T}\left(Z_{li}- Z_{lj}\right)\right\} \]
      • \((H^*_{li}, Z_{li}), (H^*_{lj}, Z_{lj})\): \(i\)th and \(j\)th outcome-covariates in \(l\)th stratum \((l= 1,\ldots, L)\)
      • Proportionality required only within stratum, not between

Software: WR::pwreg()

  • Basic syntax for PW\((\mathcal W_{\rm P})\)
    • (ID, time, status): same as WR::WRrec()
    • Z: covariate matrix; strata: possible stratifier (categorical)
library(WR)
# fit PW model (death > nonfatal event)
obj <- pwreg(ID, time, status, Z, strata = NULL)
  • Output: an object of class pwreg
    • obj$beta: \(\hat\beta\)
    • obj$Var: \(\hat\var(\hat\beta)\)
    • print(obj) to summarize regression results

Software: WR::score.proc()

  • Checking proportionality
    • obj: a pwreg object
# compute covariate-specific cumulative residuals
score.obj <- score.proc(obj)
  • Output: an object of class score.proc
    • score.obj$t: \(t\)
    • score.obj$score: a matrix with rescaled residual process for each covariate per row
    • plot(score.obj, k): plot the rescaled residuals for \(k\)th covariate

HF-ACTION: Non-Ischemic

  • Study information
    • Population: 451 non-ischemic HF patients in HF-ACTION
    • Outcome: death > (first) hospitalization
    • Covariates: treatment, age, sex, race, BMI, LVEF, histories of hypertension, COPD, diabetes, current use of ACE inhibitor, \(\beta\)-blocker, smoking status
library(WR)
head(non_ischemic)
#>   ID time status trt_ab age sex Black.vs.White Other.vs.White   bmi
#> 1  1  221      2      0  62   1              0              0 25.18
#> 2  1  383      0      0  62   1              0              0 25.18
#> 3  2   23      2      0  75   1              1              0 22.96
#> 4  2 1400      0      0  75   1              1              0 22.96
#> ...

HF-ACTION: Table One

Table 1. Patient characteristics in non-ischemic cohort of HF-ACTION
Usual care (N=231) Training (N=220)
Age (years) 56 (46, 65.5) 54 (46, 62.2)
Sex - Female 153 (66.2%) 121 (55%)
Sex - Male 78 (33.8%) 99 (45%)
Race - White 117 (50.6%) 111 (50.5%)
Race - Black 103 (44.6%) 101 (45.9%)
Race - Other 11 (4.8%) 8 (3.6%)
BMI 31.3 (26.3, 37.2) 31 (25.8, 36.5)
LVEF (%) 25.1 (20.9, 31.3) 25.1 (20.9, 31.2)
Hypertension 129 (55.8%) 129 (58.6%)
COPD 21 (9.1%) 15 (6.8%)
Diabetes 71 (30.7%) 58 (26.4%)
ACE Inhibitor 174 (75.3%) 167 (75.9%)
Beta Blocker 223 (96.5%) 211 (95.9%)

HF-ACTION: PW Regression

  • Fit PW(\(\mathcal W_{\rm P}\))
    • Death > (first) hospitalization
# number of covariates (-c(ID, time, status))
p <- ncol(non_ischemic) - 3

# extract ID, time, status and covariates matrix Z from the data.
# note that: ID, time and status should be column vector
ID <- non_ischemic[,"ID"]
time <- non_ischemic[,"time"] / 30.5 # days to months
status <- non_ischemic[,"status"]
Z <- as.matrix(non_ischemic[, 4:(3+p)])

# pass the parameters into the function
obj <- pwreg(ID, time, status, Z)

HF-ACTION: Results (I)

  • Model summary
obj
#> Call:
#> pwreg(ID = ID, time = time, status = status, Z = Z)

#> Total number of pairs: 101475 
#> Wins-losses on death:  7644 (7.5%) 
#> Wins-losses on non-fatal event:  78387 (77.2%) 
#> Indeterminate pairs 15444 (15.2%) 
#> 
#> Newton-Raphson algorithm converged in 5 iterations.
#> 
#> Overall test: chisq test with 13 degrees of freedom; 
#>  Wald statistic 24.9 with p-value 0.02392931

HF-ACTION: Results (II)

  • Inference table for \(\hat\beta\)
    • Age, black vs white, LVEF significant
obj
#>                     Estimate         se z.value p.value  
#> Training vs Usual  0.1906687  0.1264658  1.5077 0.13164  
#> Age (year)        -0.0128306  0.0057285 -2.2398 0.02510 *
#> Male vs Female    -0.1552923  0.1294198 -1.1999 0.23017  
#> Black vs White    -0.3026335  0.1461330 -2.0709 0.03836 *
#> Other vs White    -0.3565390  0.3424360 -1.0412 0.29779  
#> BMI               -0.0181310  0.0097582 -1.8580 0.06316 .
#> LVEF               0.0214905  0.0086449  2.4859 0.01292 *
#> Hypertension      -0.0318291  0.1456217 -0.2186 0.82698  
#> COPD              -0.4023069  0.2066821 -1.9465 0.05159 .
#> Diabetes           0.0703990  0.1419998  0.4958 0.62006  
#> ACE Inhibitor     -0.1068201  0.1571317 -0.6798 0.49662  
#> Beta Blocker      -0.5344979  0.3289319 -1.6250 0.10417  
#> Smoker            -0.0602350  0.1682826 -0.3579 0.72039

HF-ACTION: Race Effect

  • Joint test \((\chi_2^2)\) on race categories
    • Black/African American, white, other
# extract estimates of (beta_4, beta_5)
beta <- matrix(obj$beta[4:5])
# extract estimated covariance matrix for (beta_4, beta_5)
Sigma <- obj$Var[4:5, 4:5]
# compute chisq statistic in quadratic form
chistats <- t(beta) %*% solve(Sigma) %*% beta  

# compare the Wald statistic with the reference
# distribution of chisq(2) to obtain the p-value
1 - pchisq(chistats, df = 2)
#>           [,1]
#> [1,] 0.1016988

HF-ACTION: Win Ratio Table

  • Covariate-specific WRs \(\exp(\hat\beta)\)
    • Training wins 21.0% more than usual care
#> Point and interval estimates for the win ratios:
#>                   Win Ratio 95% lower CL 95% higher CL
#> Training vs Usual 1.2100585    0.9444056     1.5504374
#> Age (year)        0.9872513    0.9762288     0.9983983
#> Male vs Female    0.8561648    0.6643471     1.1033663
#> Black vs White    0.7388699    0.5548548     0.9839127
#> Other vs White    0.7000951    0.3578286     1.3697431
#> BMI               0.9820323    0.9634287     1.0009952
#> LVEF              1.0217231    1.0045572     1.0391823
#> Hypertension      0.9686721    0.7281543     1.2886357
#> COPD              0.6687755    0.4460178     1.0027865
#> Diabetes          1.0729362    0.8122757     1.4172433
#> ACE Inhibitor     0.8986873    0.6604773     1.2228110
#> Beta Blocker      0.5859634    0.3075270     1.1164977
#> Smoker            0.9415433    0.6770144     1.3094312

HF-ACTION: Residual Analysis

  • Check proportionality assumption on covariates
# compute score processes
score_obj <- score.proc(obj)
# plot scores for first 8 covariates
par(mfrow = c(2, 4))
for(i in c(1 : 8)){
  plot(score_obj, k = i, xlab = "Time (months)")
  # add reference lines
  abline(a = 2, b = 0, lty = 3)
  abline(a = 0, b = 0, lty = 3)
  abline(a = - 2, b = 0, lty = 3)
}

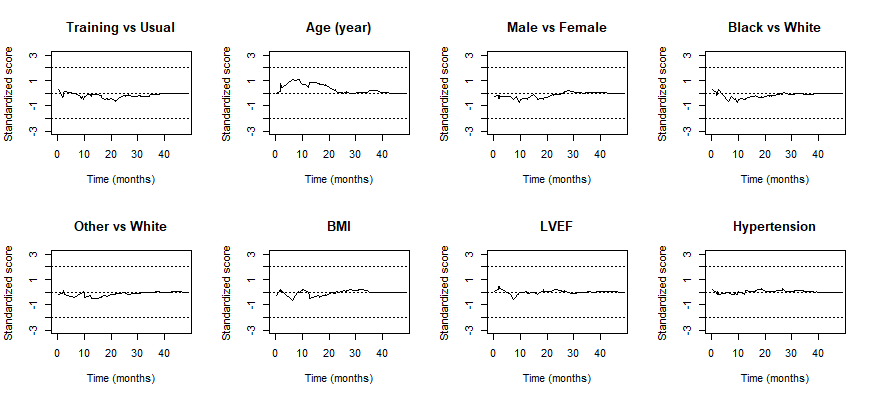
HF-ACTION: Residual Plot

  • Mostly well-behaved
    • Exercise: Fit stratified PW model by sex

Regularized Regression

Standard Model-Fitting

  • Estimating equation \[\begin{equation} U_n(\beta) = |\mathcal R|^{-1} \sum_{(i, j)\in \mathcal R} z_{ij} \left\{ \delta_{ij} - \frac{\exp(\beta^\top z_{ij})}{1 + \exp(\beta^\top z_{ij})} \right\} \end{equation}\]
    • \(z_{ij} = z_i - z_j\): covariate difference
    • \(\delta_{ij} = \mathcal{W}(\bs Y_i, \bs Y_j)(X_i \wedge X_j)\): observed win indicator
    • \(\mathcal{R}=\{(i, j): \delta_{ij} + \delta_{ji} > 0\}\): set of comparable pairs
  • High-dimensional \(z\)?
    • Variable selection
    • Improve generalizability

Regularized PW model

  • Objective function (Mao, 2025; Zou & Hastie, 2005): \[\begin{align}\label{eq:obj_fun} l_n(\beta;\lambda) &= - |\mathcal R|^{-1}\sum_{(i, j)\in\mathcal R}\left[\delta_{ij}\beta^\T z_{ij} - \log\{1+\exp(\beta^\T z_{ij})\}\right]\notag\\ &\hspace{3em}+\lambda\left\{(1-\alpha)||\beta||_2^2/2+\alpha||\beta||_1\right\} \end{align}\]
    • Pathwise solution \(\hat\beta(\lambda) = \arg\min_\beta l_n(\beta;\lambda)\)
      • Numerically equivalent to regularized logistic regression
    • Tuning parameter \(\lambda\geq 0\)—determined by cross-validation (CV)
      • \(\partial l_n(\beta; 0)/\partial\beta = U_n(\beta)\)
    • Mixing parameter \(\alpha \in (0, 1)\)
      • \(\alpha > 0\) \(\longrightarrow\) some components of \(\hat\beta(\lambda)=0\) (performs variable selection)

Pathwise Solution

  • Pathwise algorithm (Friedman et al., 2010)

    • Efficient computation of \(\hat\beta(\lambda)\) for all \(\lambda\)
    glmnet::glmnet(x, y, family = "binomial", intercept = FALSE, lambda)
    • x: covariate matrix containing \(z_{ij}\) ,
    • y: response vector \(\delta_{ij}\)
    • intercept = FALSE removes intercept
    • lambda: user-specified \(\lambda\) vector

Cross Validation

  • CV routine for logistic regression cv.glmnet()
    • Partition pairs into \(k\) folds—train and validate
    • Built-in cv.glmnet()
    • Not appropriate
      • Overlap between analysis and validation sets
      • Inflation of sample size
  • Subject-based CV
    • Partition subjects into \(k\) folds \(\mathcal{S}^{(k)}\)
    • Train on \(\mathcal{S}^{(-k)}\): \(\hat\beta^{(-k)}(\lambda)\) \(\longrightarrow\) validate on \(\mathcal{S}^{(k)}\)
    • Identify optimal \(\lambda\) maximizing average concordance index

Win/Risk Score

  • Motivation
    • Model-predicted win probability given comparability \[\mu(z_i, z_j;\beta)=\frac{\exp\{\beta^\T(z_i-z_j)\}}{1 + \exp\{\beta^\T(z_i-z_j)\}}\]
    • \(\beta^\T z\) measures tendency to win \[\begin{align*} \mu(z_i, z_j;\beta) > 0.5 &\Leftrightarrow \beta^\T z_i > \beta^\T z_j;\\ \mu(z_i, z_j;\beta) = 0.5 &\Leftrightarrow \beta^\T z_i = \beta^\T z_j;\\ \mu(z_i, z_j;\beta) < 0.5 &\Leftrightarrow \beta^\T z_i < \beta^\T z_j. \end{align*}\]
    • \(-\beta^\T z\): risk score

Generalized Concordance Index

  • Validation/test set \(\mathcal S^*\)
    • Pairwise indices \[ \mathcal R^* = \{(i,j): \delta_{ij}+\delta_{ji}\neq 0; i<j; i,j\in\S^*\} \]
  • Concordance (Cheung et al., 2019; Harrell et al., 1982; Uno et al., 2011)
    • Proportion of correct ranking of pairs \[\begin{equation}\label{eq:c_index} \mathcal C(\S^*;\beta) = |\mathcal R^*|^{-1}\sum_{(i, j)\in\mathcal R^*} \bigl[\underbrace{I\{(2\delta_{ij} -1)(\beta^\T z_i - \beta^\T z_j)>0\}}_{\text{Concordant pair}}+2^{-1} \underbrace{I(\beta^\T z_i = \beta^\T z_j)}_{\text{Tied score}}\bigr] \end{equation}\]

Validation and Testing

  • Model tuning
    • \(k\)th-fold CV concordance: \(C^{(k)}(\lambda) = \mathcal C\left(\Sk;\wh\beta^{(-k)}(\lambda)\right)\)
    • Optimal \(\lambda_{\rm opt} = \arg\max_\lambda K^{-1}\sum_{k=1}^K\C^{(k)}(\lambda)\)
    • Final model: \(\wh\beta(\lambda_{\rm opt})\)
  • Variable importance
    • Component-wise \(|\beta|/\text{sd}(z)\)
  • Test C-index
    • \(\mathcal C(\S^*;\wh\beta(\lambda_{\rm opt}))\) for test set \(\S^*\)

Workflow - Input Data

  • Data format

    • Long format with columns: id, time, status, and covariates
    # Load package containing data
library(WR)
df <- gbc # n = 686 subjects, p = 9 covariates
df # status = 0 (censored), 1 (death), 2 (recurrence)
#>   id      time status hormone age menopause size grade ...
#>1   1 43.836066      2       1  38         1   18     3  
#>2   1 74.819672      0       1  38         1   18     3  
#>3   2 46.557377      2       1  52         1   20     1   
#>4   2 65.770492      0       1  52         1   20     1  
#>5   3 41.934426      2       1  47         1   30     2   
#>...

Workflow - Data Partitioning

  • Splitting data
    • wr_split() function
# Data partitioning ------------------------------------
set.seed(123)
obj_split <- df |> wr_split(prop = 0.8) # 80% training, 20% test
# Take training and test set
df_train <- obj_split$df_train
df_test <- obj_split$df_test

Workflow - Cross-Validation (I)

  • \(k\)-fold CV
    • cv_wrnet(id, time, status, Z, k = 10, ...)
# 10-fold CV -------------------------------------------
set.seed(1234)
obj_cv <- cv_wrnet(df_train$id, df_train$time, df_train$status, 
                    df_train |> select(-c(id, time, status)))
# Plot CV results (C-index vs log-lambda)
obj_cv |> 
   ggplot(aes(x =  log(lambda), y = concordance)) +
   geom_point() + geom_line() + theme_minimal()
# Optimal lambda
lambda_opt <- obj_cv$lambda[which.max(obj_cv$concordance)]
lambda_opt
#> [1] 0.0171976

Workflow - Cross-Validation (II)

  • Validation C-index

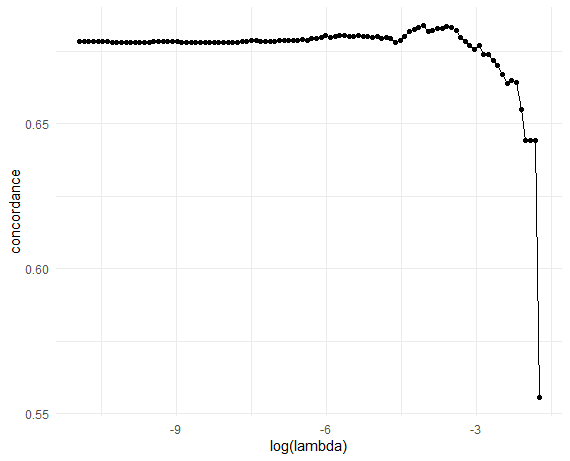
Workflow - Final Model

  • Fit final model

    • wrnet(id, time, status, Z, lambda = lambda_opt, ...)
    # Final model ------------------------------------------
final_fit <- wrnet(df_train$id, df_train$time, df_train$status, 
          df_train |> select(-c(id, time, status)), lambda = lambda_opt)
final_fit$beta # Estimated coefficients
#>                      s0
#> hormone     0.306026364
#> age         0.003111462
#> menopause   .          
#> size       -0.007720497
#> grade      -0.285511701
#> nodes      -0.082227827
#> prog_recp   0.001861367
#> estrg_recp  .

Workflow - Variable Importance

  • Variable importance
final_fit |> vi_wrnet() |> vip()

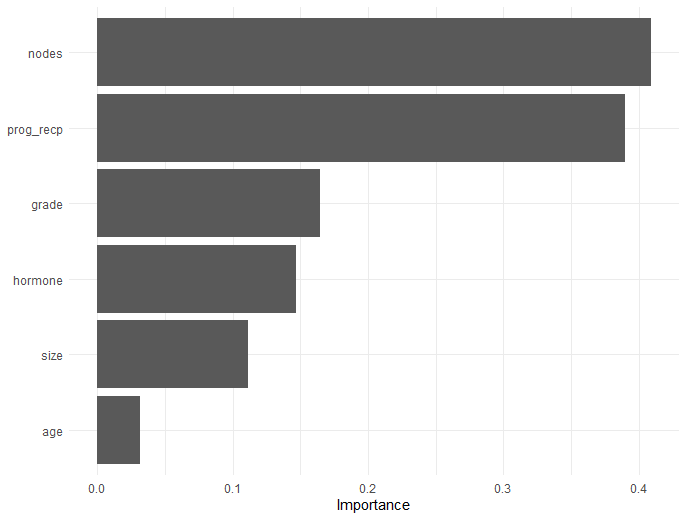
Workflow - Test Performance

  • Overall and component-wise C-index
    • test_wrnet(final_fit, df_test)
# Test model performance -------------------------------
test_result <- final_fit |> test_wrnet(df_test)
# Overall and event-specific C-indices
test_result$concordance
#> # A tibble: 3 × 2
#>   component concordance
#>   <chr>           <dbl>
#> 1 death           0.724
#> 2 nonfatal        0.607
#> 3 overall         0.664

Conclusion

Notes

  • More on PW

    • Check functional form (linear, quadratic, grouped) of \(Z\) (Lin et al., 1993)

      • E.g., is age effect linear?

      \[ \mbox{plot} \sum_{i, j: Z_i - Z_j\leq z}(Z_i - Z_j)M_{ij}(\infty \mid Z_i, Z_j;\hat\beta) \mbox{ against } z\in\mathbb R \]

    • Currently WR::pwreg() implements only PW(\(\mathcal W_{\rm P}\))

      • More functionalities to be added

    • Variations: regression of win ratio/odds (Follmann et al., 2019; Song et al., 2022)

Summary

  • PW: WR regression
    • Proportionality and multiplicativity \[ WR(t\mid Z_i, Z_j;\mathcal W)=\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\} \]
      • \(\exp(\beta)\): WRs with unit increases in covariates
      • WR::pwreg(ID, time, status, Z, strata)
  • Regularized PW

References

Cheung, L. C., Pan, Q., Hyun, N., & Katki, H. A. (2019). Prioritized concordance index for hierarchical survival outcomes. Statistics in Medicine, 38(15), 2868–2882.
Dong, G., Hoaglin, D. C., Huang, B., Cui, Y., Wang, D., Cheng, Y., & Gamalo-Siebers, M. (2023). The stratified win statistics (win ratio, win odds, and net benefit). Pharmaceutical Statistics, 22(4), 748–756. https://doi.org/10.1002/pst.2293
Dong, G., Qiu, J., Wang, D., & Vandemeulebroecke, M. (2017). The stratified win ratio. Journal of Biopharmaceutical Statistics, 28(4), 778–796. https://doi.org/10.1080/10543406.2017.1397007
Follmann, D., Fay, M. P., Hamasaki, T., & Evans, S. (2019). Analysis of ordered composite endpoints. Statistics in Medicine, 39(5), 602–616. https://doi.org/10.1002/sim.8431
Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1), 1.
Harrell, F. E., Califf, R. M., Pryor, D. B., Lee, K. L., & Rosati, R. A. (1982). Evaluating the yield of medical tests. JAMA, 247(18), 2543–2546.
Lin, D. Y., Wei, L. J., & Ying, Z. (1993). Checking the Cox model with cumulative sums of martingale-based residuals. Biometrika, 80(3), 557–572. https://doi.org/10.1093/biomet/80.3.557
Mao, L. (2025). Regularized win ratio regression for variable selection and risk prediction, with an application to a cardiovascular trial. BMC Medical Research Methodology, 25(1). https://doi.org/10.1186/s12874-025-02554-w
Mao, L., & Wang, T. (2021). A class of proportional win-fractions regression models for composite outcomes. Biometrics, 77(4), 1265–1275. https://doi.org/10.1111/biom.13382
Song, J., Verbeeck, J., Huang, B., Hoaglin, D. C., Gamalo-Siebers, M., Seifu, Y., Wang, D., Cooner, F., & Dong, G. (2022). The win odds: statistical inference and regression. Journal of Biopharmaceutical Statistics, 33(2), 140–150. https://doi.org/10.1080/10543406.2022.2089156
Uno, H., Cai, T., Pencina, M. J., D’Agostino, R. B., & Wei, L.-J. (2011). On the c-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine, 30(10), 1105–1117.
Wang, T., & Mao, L. (2022). Stratified proportional win-fractions regression analysis. Statistics in Medicine, 41(26), 5305–5318. https://doi.org/10.1002/sim.9570
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology, 67(2), 301–320.