How to perform efficient simulations in Tidyverse

Use purrr::map() for element-wise operations

General steps

1. Generate multiple datasets: Simulate \(N\) datasets based on a defined data-generating process.
2. Apply a statistical method: For each dataset, apply the same statistical method (e.g., linear regression, hypothesis testing).
3. Summarize the results: Aggregate and summarize performance metrics (e.g., bias, MSE, coverage).

Example: linear regression

Consider a simulation study for linear regression.

# Load library
library(tidyverse)

Define the data-generating process

Simulate a dataset for linear regression:

generate_data <- function(n = 100, beta0 = 1, beta1 = 2, sigma = 1) {
  tibble(
    x = rnorm(n),
    y = beta0 + beta1 * x + rnorm(n, sd = sigma)
  )
}

Define the statistical method

Fit a linear model and extract the coefficient estimates:

fit_model <- function(data) {
  model <- lm(y ~ x, data = data)
  tibble(
    beta0_hat = coef(model)[1],
    beta1_hat = coef(model)[2]
  )
}

Perform simulation

Generate \(N = 1000\) datasets, each with an id (sim_id) and stored in a list-valued column data.

set.seed(123)

# Number of simulations
N <- 1000

# Simulate data
simulated_data <- tibble(
  sim_id = 1:N
) %>%
  mutate(
    data = map(sim_id, ~ generate_data(n = 100, beta0 = 1, beta1 = 2, sigma = 1)) # Generate datasets
  )

# Take a look
simulated_data
#> # A tibble: 1,000 × 2
#>     sim_id data              
#>      <int> <list>            
#>   1      1 <tibble [100 × 2]>
#>   2      2 <tibble [100 × 2]>
#>   3      3 <tibble [100 × 2]>
#>   4      4 <tibble [100 × 2]>
#>   5      5 <tibble [100 × 2]>
#>   6      6 <tibble [100 × 2]>
#>   7      7 <tibble [100 × 2]>
#>   8      8 <tibble [100 × 2]>
#>   9      9 <tibble [100 × 2]>
#>  10     10 <tibble [100 × 2]>
#>  # ℹ 990 more rows
#>  # ℹ Use `print(n = ...)` to see more rows

Use purrr::map() to fit a linear model to each entry of data and store the results in a list-valued column results. Then unnest to combine all results into a single table.

# Fit model to each simulated dataset
simulation_results <- simulated_data %>%
  mutate(
   results = map(data, fit_model) # Apply the model
  ) %>%
  unnest(results) # Combine all results into a single table

## Take a look
simulation_results
#> # A tibble: 1,000 × 4
#>    sim_id data               beta0_hat beta1_hat
#>     <int> <list>                 <dbl>     <dbl>
#>  1      1 <tibble [100 × 2]>     0.897      1.95
#>  2      2 <tibble [100 × 2]>     0.970      1.95
#>  3      3 <tibble [100 × 2]>     0.937      2.20
#>  4      4 <tibble [100 × 2]>     1.11       2.00
#>  5      5 <tibble [100 × 2]>     0.983      1.98
#>  6      6 <tibble [100 × 2]>     0.979      2.02
#>  7      7 <tibble [100 × 2]>     0.940      1.99
#>  8      8 <tibble [100 × 2]>     1.04       1.96
#>  9      9 <tibble [100 × 2]>     1.03       1.98
#> 10     10 <tibble [100 × 2]>     1.08       1.94
#> # ℹ 990 more rows
#> # ℹ Use `print(n = ...)` to see more rows

Summarize the results

# Summarize the results
summary_stats <- simulation_results %>%
  summarize(
    beta0_mean = mean(beta0_hat),
    beta1_mean = mean(beta1_hat),
    beta0_bias = mean(beta0_hat - 1),
    beta1_bias = mean(beta1_hat - 2),
    beta0_sd = sd(beta0_hat),
    beta1_sd = sd(beta1_hat)
  )

summary_stats
#> # A tibble: 1 × 6
#>   beta0_mean beta1_mean beta0_bias beta1_bias beta0_sd beta1_sd
#>        <dbl>      <dbl>      <dbl>      <dbl>    <dbl>    <dbl>
#> 1       1.00       2.00    0.00336    0.00357    0.102    0.103

Visualize the results (optional)

# Histogram of beta1 estimates
ggplot(simulation_results, aes(x = beta1_hat)) +
  geom_histogram(bins = 30, fill = "skyblue", color = "black") +
  geom_vline(xintercept = 2, linetype = "dashed", color = "red") +
  labs(
    title = "Distribution of Beta1 Estimates",
    x = "Beta1 Estimates",
    y = "Frequency"
  ) +
  theme_minimal()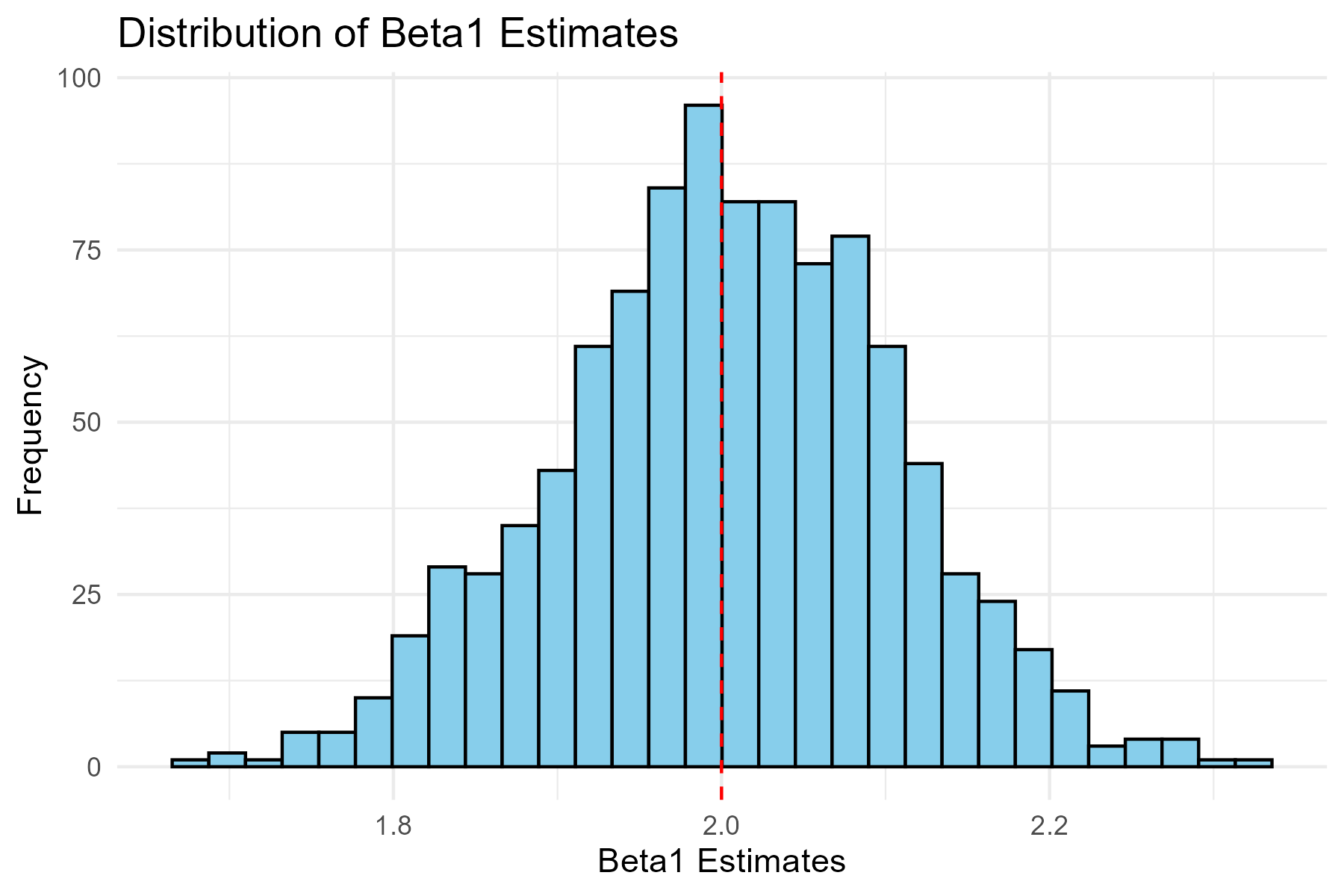

Key features of workflow

1. Reproducibility:
   • Use set.seed() for consistent results.
2. Scalability:
   • Adjust N to increase or decrease the number of datasets.
3. Summarization:
   • map() and unnest() make it easy to handle multiple datasets and their outputs.
4. Customization:
   • Replace the data-generating process or statistical method to fit your needs.