WRNet: Regularized win ratio regression

Variable selection and risk prediction with hierarchical composite outcomes

Lu Mao

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

\[ \newcommand{\wh}{\widehat} \newcommand{\wt}{\widetilde} \def\bs{\boldsymbol} \newcommand{\red}{} \newcommand{\indep}{\perp \!\!\! \perp} \def\T{{ \mathrm{\scriptscriptstyle T} }} \def\pr{{\rm pr}} \def\d{{\rm d}} \def\W{{\mathcal W}} \def\H{{\mathcal H}} \def\I{{\mathcal I}} \def\C{{\mathcal C}} \def\S{{\mathcal S}} \def\Sk{{\mathcal S}^{(k)}} \def\Skm{{\mathcal S}^{(-k)}} \def\v{\varepsilon} \def\bSig\mathbf{\Sigma} \def\Un{\sum_{i=1}^{n-1}\sum_{j=i+1}^n} \]

Outline

  • Introduction
  • Methods
    • Standard win ratio regression
    • Regularization and computation
    • WRNet workflow
  • Simulation studies
  • HF-ACTION application

Introduction

Hierarchical Composite Endpoints

  • Composite outcomes
    • Components: Death, hospitalization, other events
    • Standard approach: Time to first event (e.g., Cox model)
  • Win ratio (WR) (Pocock et al., 2012)
    • Pairwise comparisons: Treatment vs control (Buyse, 2010)
    • Each pair: Death > hospitalization (> other events)
    • Effect size \[ \text{WR} = \frac{\text{Number of wins}}{\text{Number of losses}} \]

Data and Notation

  • Outcomes data (subject \(i\))
    • \(D_i\): time to death
    • \(T_i\): time to first nonfatal event
    • \(\bs Y_i(t) =(D_i\wedge t, T_i\wedge t)\): cumulative data at \(t\)
      • \(x\wedge y = \min(x, y)\)
  • Win indicator \[\begin{align*}\label{eq:win2tier} \W(\bs Y_i, \bs Y_j)(t) = \underbrace{I(D_j< D_i\wedge t)}_{\mbox{Win on survival}} + \underbrace{I(D_i\wedge D_j >t,\; T_j< T_i\wedge t)}_ {\mbox{Tie on survival, win on nonfatal event}} \end{align*}\]

Win Ratio Regression

  • Semiparametric regression \[\begin{equation}\label{eq:pw} \frac{\pr\{\W(\bs Y_i, \bs Y_j)(t) = 1\mid z_i, z_j\}}{\pr\{\W(\bs Y_j, \bs Y_i)(t) = 1\mid z_j, z_i\}} = \exp\left\{\beta^\T(z_i - z_j)\right\} \end{equation}\]
    • \(z\): \(p\)-dimensional covariates
    • Proportional win-fractions (PW) model
      • Equivalent to Cox PH model in univariate case (Oakes, 2016)—WR = 1/HR
    • \(\exp(\beta)\): win ratios associated with unit increases in \(z\)
  • Limitation: \(p<< n\)

Goals

  • Objectives:
    • Automate variable selection in WR regression
    • Enhance prediction accuracy and model parsimony
  • Approach:
    • Apply elastic net regularization to PW model
      • Mixture of \(L_1\) (lasso) and \(L_2\) (ridge) penalties
    • Implemented in wrnet R package

Methods

Standard Model-Fitting

  • Observed data
    • \(\bs Y_i(X_i)\): outcomes data up to \(X_i = D_i \wedge C_i\) (\(C_i\): censoring time)
  • Estimating equation (Mao & Wang, 2021) \[\begin{equation} U_n(\beta) = |\mathcal R|^{-1} \sum_{(i, j)\in \mathcal R} z_{ij} \left\{ \delta_{ij} - \frac{\exp(\beta^\top z_{ij})}{1 + \exp(\beta^\top z_{ij})} \right\} \end{equation}\]
    • \(z_{ij} = z_i - z_j\): covariate difference
    • \(\delta_{ij} = \mathcal{W}(\bs Y_i, \bs Y_j)(X_i \wedge X_j)\): observed win indicator
    • \(\mathcal{R}=\{(i, j): \delta_{ij} + \delta_{ji} > 0\}\): set of comparable pairs

Estimation

  • Estimator: solving \[ U_n(\hat\beta) \;\;= 0 \]
    • Standard Newton–Raphson algorithm
  • Connection with logistic regression
    • \(U_n(\hat\beta)\) equivalent to logistic score function (no intercept)
    • Each comparable \((i, j)\) pair as an observation
      • \(\delta_{ij}\): binary response
      • \(z_{ij}\): covariates

Regularized PW model

  • Objective function (Zou & Hastie, 2005): \[\begin{align}\label{eq:obj_fun} l_n(\beta;\lambda) &= - |\mathcal R|^{-1}\sum_{(i, j)\in\mathcal R}\left[\delta_{ij}\beta^\T z_{ij} - \log\{1+\exp(\beta^\T z_{ij})\}\right]\notag\\ &\hspace{3em}+\lambda\left\{(1-\alpha)||\beta||_2^2/2+\alpha||\beta||_1\right\} \end{align}\]
    • Pathwise solution \(\hat\beta(\lambda) = \arg\min_\beta l_n(\beta;\lambda)\)
      • Numerically equivalent to regularized logistic regression
    • Tuning parameter \(\lambda\geq 0\)—determined by cross-validation (CV)
      • \(\partial l_n(\beta; 0)/\partial\beta = U_n(\beta)\)
    • Mixing parameter \(\alpha \in (0, 1)\)
      • \(\alpha > 0\) \(\longrightarrow\) some components of \(\hat\beta(\lambda)=0\) (performs variable selection)

Pathwise Solution

  • Pathwise algorithm (Friedman et al., 2010)

    • Efficient computation of \(\hat\beta(\lambda)\) for all \(\lambda\)
    glmnet::glmnet(x, y, family = "binomial", intercept = FALSE, lambda)
    • x: covariate matrix containing \(z_{ij}\) ,
    • y: response vector \(\delta_{ij}\)
    • intercept = FALSE removes intercept
    • lambda: user-specified \(\lambda\) vector

Cross Validation

  • CV routine for logistic regression cv.glmnet()
    • Partition pairs into \(k\) folds—train and validate
    • Built-in cv.glmnet()
    • Not appropriate
      • Overlap between analysis and validation sets
      • Inflation of sample size
  • Subject-based CV
    • Partition subjects into \(k\) folds \(\mathcal{S}^{(k)}\)
    • Train on \(\mathcal{S}^{(-k)}\): \(\wh\beta^{(-k)}(\lambda)\) \(\longrightarrow\) validate on \(\mathcal{S}^{(k)}\)
    • Identify optimal \(\lambda\) maximizing average concordance index

Win/Risk Score

  • Motivation
    • Model-predicted win probability given comparability \[\mu(z_i, z_j;\beta)=\frac{\exp\{\beta^\T(z_i-z_j)\}}{1 + \exp\{\beta^\T(z_i-z_j)\}}\]
    • \(\beta^\T z\) measures tendency to win \[\begin{align*} \mu(z_i, z_j;\beta) > 0.5 &\Leftrightarrow \beta^\T z_i > \beta^\T z_j;\\ \mu(z_i, z_j;\beta) = 0.5 &\Leftrightarrow \beta^\T z_i = \beta^\T z_j;\\ \mu(z_i, z_j;\beta) < 0.5 &\Leftrightarrow \beta^\T z_i < \beta^\T z_j. \end{align*}\]
    • \(-\beta^\T z\): risk score

Generalized Concordance Index

  • Validation/test set \(\mathcal S^*\)
    • Pairwise indices \[ \mathcal R^* = \{(i,j): \delta_{ij}+\delta_{ji}\neq 0; i<j; i,j\in\S^*\} \]
  • Concordance (Cheung et al., 2019; Harrell et al., 1982; Uno et al., 2011)
    • Proportion of correct ranking of pairs \[\begin{equation}\label{eq:c_index} \mathcal C(\S^*;\beta) = |\mathcal R^*|^{-1}\sum_{(i, j)\in\mathcal R^*} \bigl[\underbrace{I\{(2\delta_{ij} -1)(\beta^\T z_i - \beta^\T z_j)>0\}}_{\text{Concordant pair}}+2^{-1} \underbrace{I(\beta^\T z_i = \beta^\T z_j)}_{\text{Tied score}}\bigr] \end{equation}\]

Validation and Testing

  • Model tuning
    • \(k\)th-fold CV concordance: \(C^{(k)}(\lambda) = \mathcal C\left(\Sk;\wh\beta^{(-k)}(\lambda)\right)\)
    • Optimal \(\lambda_{\rm opt} = \arg\max_\lambda K^{-1}\sum_{k=1}^K\C^{(k)}(\lambda)\)
    • Final model: \(\wh\beta(\lambda_{\rm opt})\)
  • Variable importance
    • Component-wise \(|\beta|/\text{sd}(z)\)
  • Test C-index
    • \(\mathcal C(\S^*;\wh\beta(\lambda_{\rm opt}))\) for test set \(\S^*\)

Workflow - Input Data

  • Data format

    • Long format with columns: id, time, status, and covariates
    # Load package containing data
library(WR)
df <- gbc # n = 686 subjects, p = 9 covariates
df # status = 0 (censored), 1 (death), 2 (recurrence)
#>   id      time status hormone age menopause size grade ...
#>1   1 43.836066      2       1  38         1   18     3  
#>2   1 74.819672      0       1  38         1   18     3  
#>3   2 46.557377      2       1  52         1   20     1   
#>4   2 65.770492      0       1  52         1   20     1  
#>5   3 41.934426      2       1  47         1   30     2   
#>...

Workflow - Data Partitioning

  • Splitting data
    • wr_split() function
# Data partitioning ------------------------------------
set.seed(123)
obj_split <- df |> wr_split(prop = 0.8) # 80% training, 20% test
# Take training and test set
df_train <- obj_split$df_train
df_test <- obj_split$df_test

Workflow - Cross-Validation (I)

  • \(k\)-fold CV
    • cv_wrnet(id, time, status, Z, k = 10, ...)
# 10-fold CV -------------------------------------------
set.seed(1234)
obj_cv <- cv_wrnet(df_train$id, df_train$time, df_train$status, 
                    df_train |> select(-c(id, time, status)))
# Plot CV results (C-index vs log-lambda)
obj_cv |> 
   ggplot(aes(x =  log(lambda), y = concordance)) +
   geom_point() + geom_line() + theme_minimal()
# Optimal lambda
lambda_opt <- obj_cv$lambda[which.max(obj_cv$concordance)]
lambda_opt
#> [1] 0.0171976

Workflow - Cross-Validation (II)

  • Validation C-index

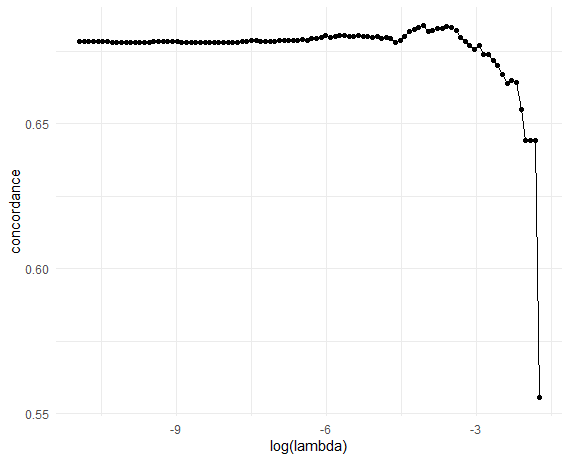
Workflow - Final Model

  • Fit final model

    • wrnet(id, time, status, Z, lambda = lambda_opt, ...)
    # Final model ------------------------------------------
final_fit <- wrnet(df_train$id, df_train$time, df_train$status, 
          df_train |> select(-c(id, time, status)), lambda = lambda_opt)
final_fit$beta # Estimated coefficients
#>                      s0
#> hormone     0.306026364
#> age         0.003111462
#> menopause   .          
#> size       -0.007720497
#> grade      -0.285511701
#> nodes      -0.082227827
#> prog_recp   0.001861367
#> estrg_recp  .

Workflow - Variable Importance

  • Variable importance
final_fit |> vi_wrnet() |> vip()

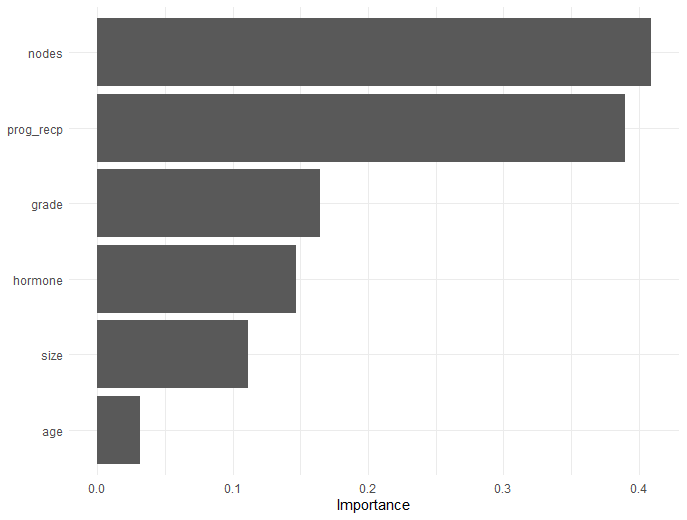
Workflow - Test Performance

  • Overall and component-wise C-index
    • test_wrnet(final_fit, df_test)
# Test model performance -------------------------------
test_result <- final_fit |> test_wrnet(df_test)
# Overall and event-specific C-indices
test_result$concordance
#> # A tibble: 3 × 2
#>   component concordance
#>   <chr>           <dbl>
#> 1 death           0.724
#> 2 nonfatal        0.607
#> 3 overall         0.664

Simulations

Setup

  • Covariates: \(z = (z_{\cdot 1}, z_{\cdot 2}, \ldots, z_{\cdot p})^\T\)
    • \(z_{\cdot k} \sim N(0,1)\)—AR(1) with \(\rho = 0.1\)
  • Outcome model: \[ \pr(D > s, T > t\mid z) = \exp\left(-\left[\{\exp(-\beta_D^\T z)\lambda_Ds\}^\kappa + \{\exp(-\beta_H^\T z)\lambda_Ht\}^\kappa\right]^{1/\kappa}\right) \]
    • \(\lambda_D = 0.1\), \(\lambda_H = 1\), \(\kappa = 1.25\)
  • Censoring: \(\mbox{Un}[0.2, 4]\wedge\mbox{Expn}(\lambda_C)\)
    • \(\lambda_C = 0.02\)

Two Effect Patterns

  • Scenarios
    1. Same effect pattern on components \[ \beta_D=\beta_H=(\underbrace{0.5,\ldots, 0.5}_{10}, \underbrace{0,\ldots, 0}_{p - 10}). \]
    2. Different effect patterns on components \[\begin{align*} \beta_D&=(\underbrace{0.75,\ldots, 0.75}_{5}, \underbrace{0,\ldots, 0}_{p - 5});\\ \beta_H&=(\underbrace{0,\ldots, 0}_{5}, \underbrace{0.75,\ldots, 0.75}_{5}, \underbrace{0,\ldots, 0}_{p - 10}) \end{align*}\]

Predictive Accuracy - C-index

  • Regularized WR vs regularized Cox on first event
    • 80% training + 20% testing

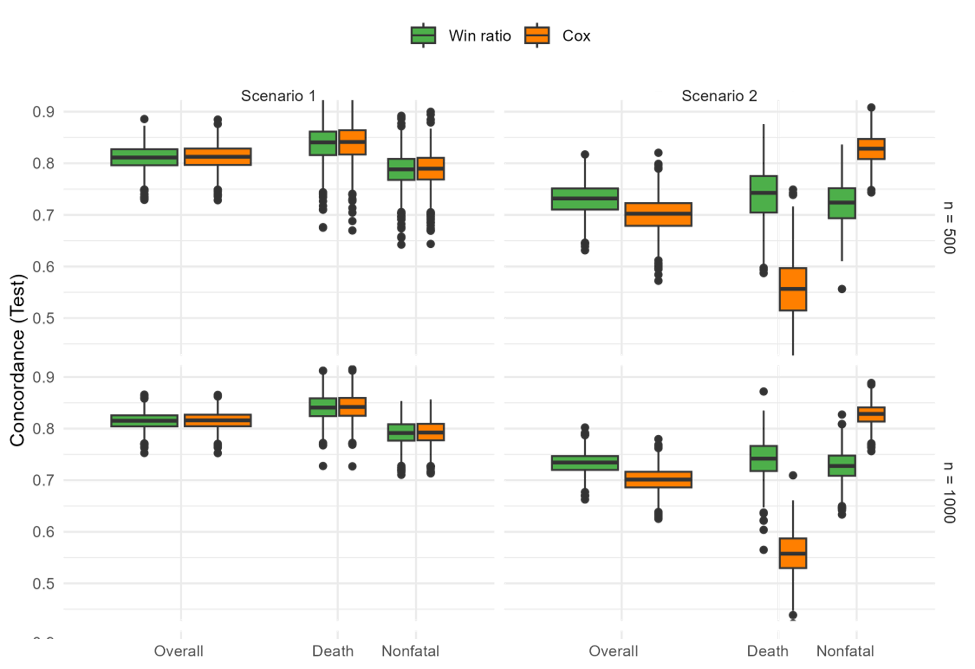
Variable Selection - Sensitivity

  • S2: \(z_{\cdot 1}\)–\(z_{\cdot 5}\) \(\longrightarrow\) mortality

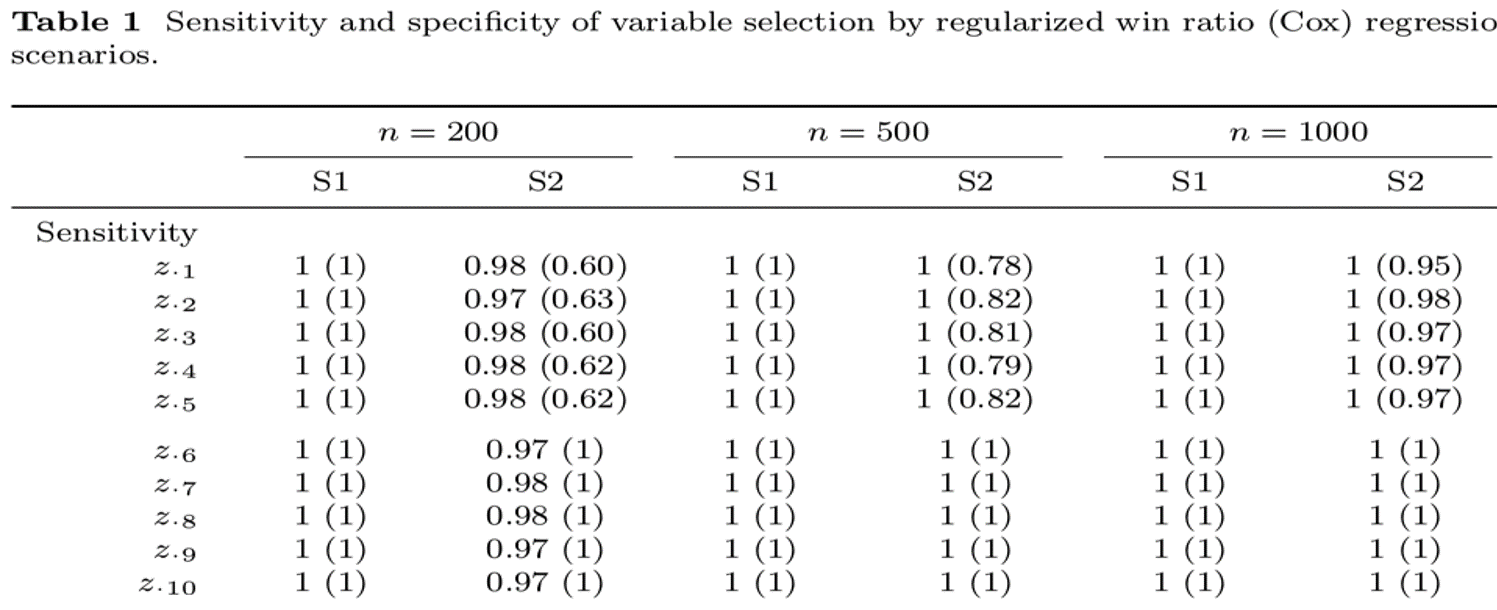
Variable Selection - Specifity

  • \(z_{\cdot 11}\)–\(z_{\cdot 20}\) \(\longrightarrow\) no effect

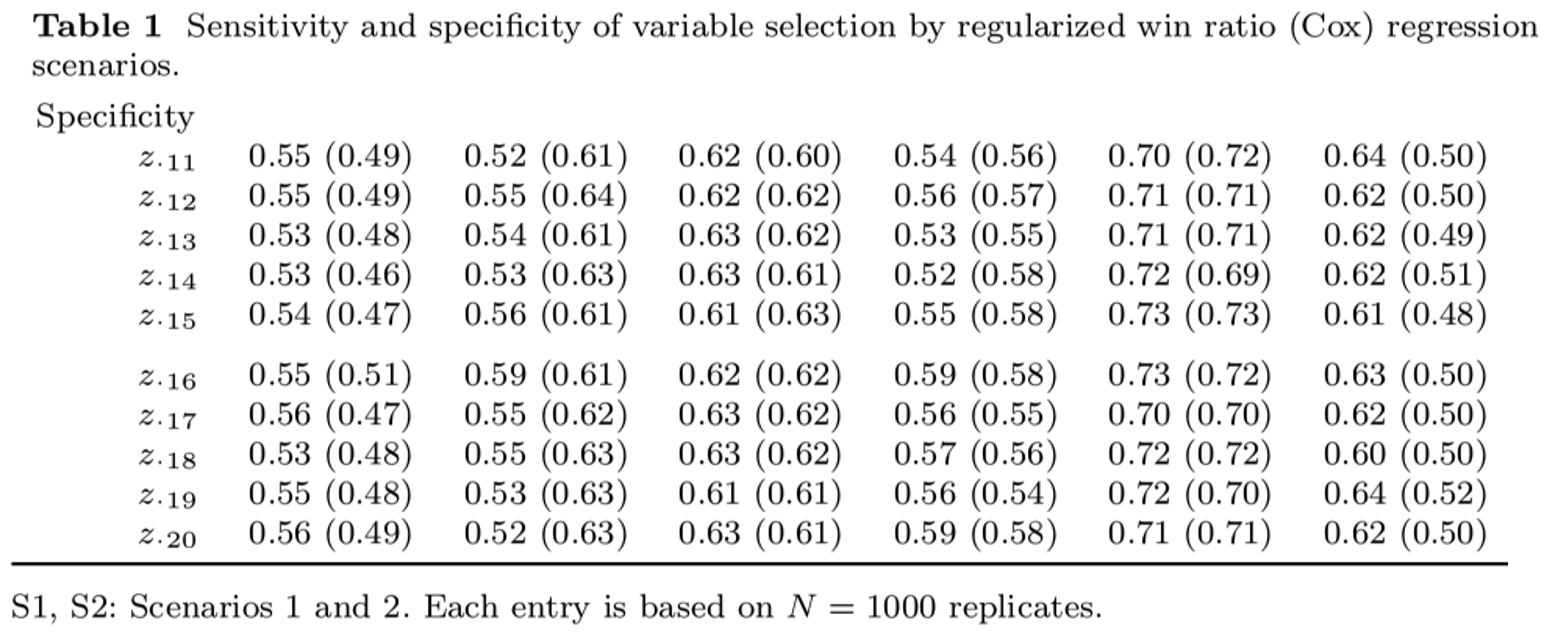
HF-ACTION Application

Study Information

  • HF-ACTION (O’Connor et al., 2009)
    • Population: 2,331 HFrEF patients across North America and France
    • Objective: Evaluate the effect of exercise training on composite of death and hospitalization
  • Subgroup of high-risk patients
    • \(n=426\) high-risk patients (CPX duration \(\leq 9\) min)
    • Outcomes: death > hospitalization
    • \(p=153\) baseline features
    • Train-test split: 80%/20%

Cross-Validation

  • Naive pairwise logistic CV on pairs leads to overfitting

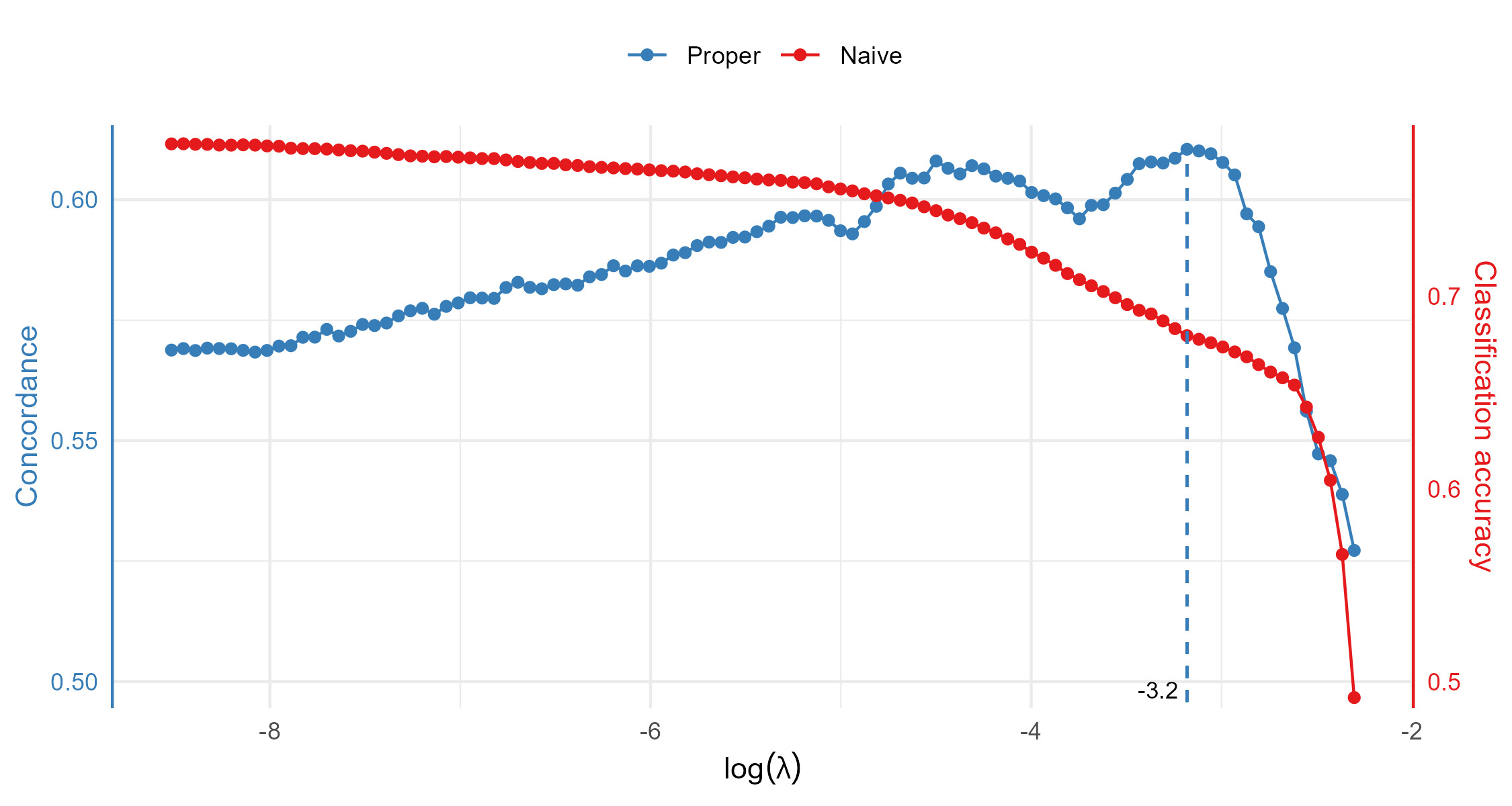
Test Performance - Risk Scores

  • WRNet vs regularized Cox
    • WRNet better stratifies high-risk patients, especially on mortality

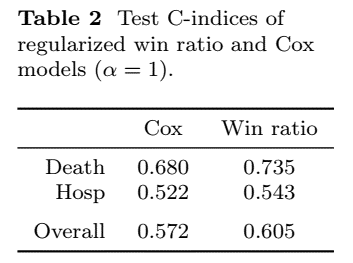
Test Performance - C-Index

  • WRNet vs regularized Cox
    • WRNet outperforms Cox on overall and event-specific C-indices

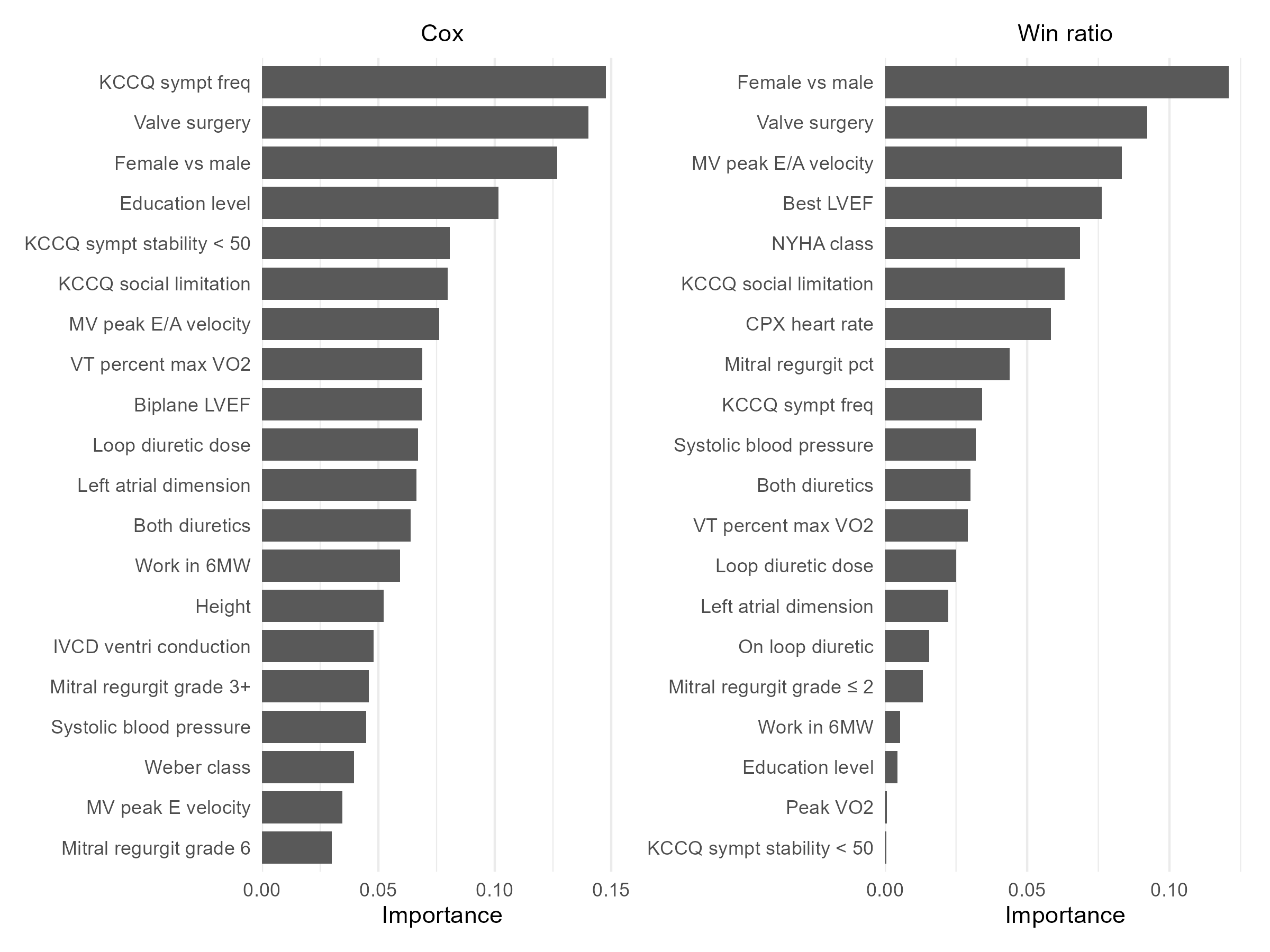
Variable Importance

  • WRNet selects 20 interpretable variables

Final WR Model

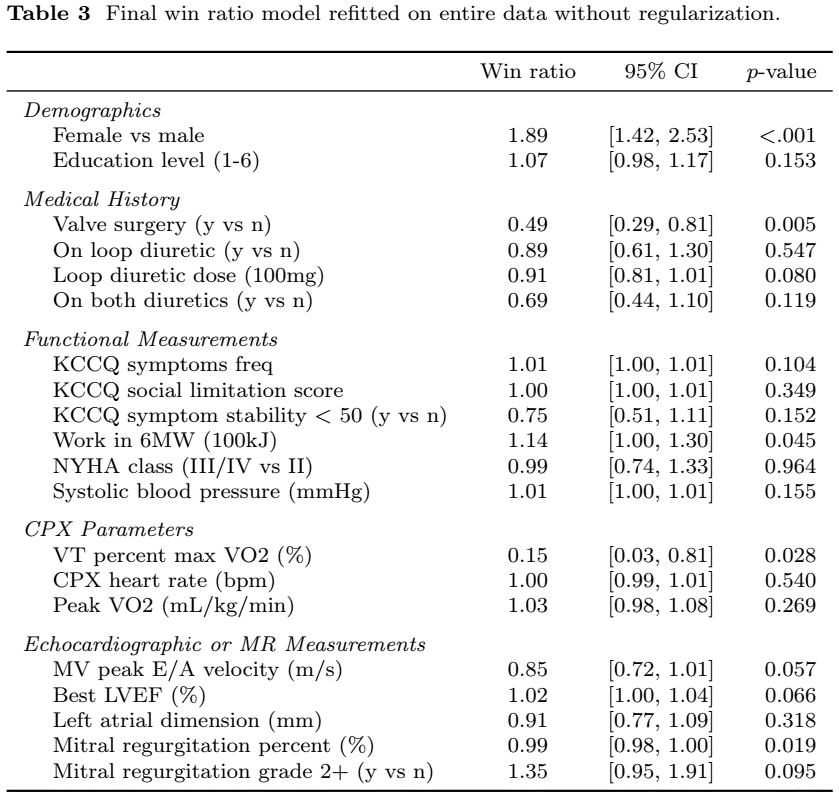
Summary and Discussion

Summary

  • Methodology
    • Developed elastic net-regularized WR regression
    • Better aligns with clinical priorities than Cox
    • Accurate feature selection and prediction
  • Tools

Future Topics

  • Explore \(\alpha \in (0,1)\) settings
  • Extend to time-varying effects and nonlinearities
  • Decision trees

References

Buyse, M. (2010). Generalized pairwise comparisons of prioritized outcomes in the two-sample problem. Statistics in Medicine, 29, 3245–3257.
Cheung, L. C., Pan, Q., Hyun, N., & Katki, H. A. (2019). Prioritized concordance index for hierarchical survival outcomes. Statistics in Medicine, 38(15), 2868–2882.
Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1), 1.
Harrell, F. E., Califf, R. M., Pryor, D. B., Lee, K. L., & Rosati, R. A. (1982). Evaluating the yield of medical tests. JAMA, 247(18), 2543–2546.
Mao, L., & Wang, T. (2021). A class of proportional win-fractions regression models for composite outcomes. Biometrics, 77(4), 1265–1275.
O’Connor, C. M., Whellan, D. J., Lee, K. L., Keteyian, S. J., Cooper, L. S., Ellis, S. J., Leifer, E. S., Kraus, W. E., Kitzman, D. W., Blumenthal, J. A., et al. (2009). Efficacy and safety of exercise training in patients with chronic heart failure: HF-ACTION randomized controlled trial. Journal of the American Medical Association, 301(14), 1439–1450.
Oakes, D. (2016). On the win-ratio statistic in clinical trials with multiple types of event. Biometrika, 103(1), 742–745.
Pocock, S., Ariti, C., Collier, T., & Wang, D. (2012). The win ratio: A new approach to the analysis of composite endpoints in clinical trials based on clinical priorities. European Heart Journal, 33(2), 176–112.
Uno, H., Cai, T., Pencina, M. J., D’Agostino, R. B., & Wei, L.-J. (2011). On the c-statistics for evaluating overall adequacy of risk prediction procedures with censored survival data. Statistics in Medicine, 30(10), 1105–1117.
Zou, H., & Hastie, T. (2005). Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology, 67(2), 301–320.