Tidy Survival Analysis: Applying R’s Tidyverse to Survival Data

Module 5. Machine Learning

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Aug 3, 2025

Machine Learning Survival Models

Setting

  • With many covariates
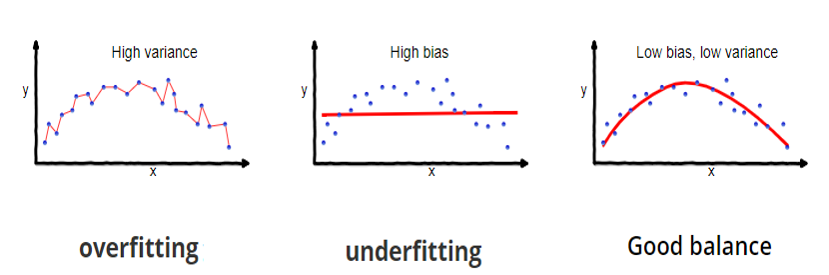
    • Prediction accuracy: under- vs over-fitting
      • Too many predictors \(\to\) overfitting
    • Interpretation: easier with fewer predictors

Regularized Cox Regression

  • Idea
    • Penalize the magnitude of coefficients (\(L^q\)-norm) to avoid overfitting
  • Elastic net: minimize objective function \[ \ell(\beta) = -\mbox{log-partial-likelihood}(\beta) + \lambda\sum_{j=1}^p\left\{\alpha|\beta_j|+2^{-1}(1-\alpha)\beta_j^2\right\} \]
    • \(\lambda\): tuning parameter that controls the strength of penalty
      • Determined by cross-validation
    • \(\alpha\): controls the type of penalty
      • \(\alpha = 0\) \(\to\) ridge regression: handles correlated predictors better
      • \(\alpha = 1\) \(\to\) lasso regression: performs variable selection
    • Implementation: glmnet package

Survival Trees

  • Decision trees
    • Classification and Regression Trees (CART; Breiman et al., 1984)
    • Root node (all sample) \(\stackrel{\rm covariates}{\rightarrow}\) split into (more homogeneous) daughter nodes \(\stackrel{\rm covariates}{\rightarrow}\) split recursively
  • Growing the tree
    • Starting with root node, search partition criteria \[Z_{\cdot j}\leq z \,\,\,(j=1,\ldots, p; z \in\mathbb R)\] for one that minimizes “impurity” (e.g., mean squared deviance residuals) within daughter nodes \[\begin{equation}\label{eq:tree:nodes} A=\{i=1,\ldots, n: Z_{ij}\leq z\} \mbox{ and } B=\{i=1,\ldots, n: Z_{ij}> z\} \end{equation}\]
    • Recursive splitting until terminal nodes sufficiently “pure” in outcome

Complexity Control and Prediction

  • Pruning the tree
    • Cut overgrown branches to prevent overfitting
    • Penalize number of terminal nodes
    • Tune complexity parameter (or minimum size of terminal node)
  • Prediction
    • New \(z\) \(\rightarrow\) terminal node \(\rightarrow\) KM estimates (or median survival)
  • Implementation: rpart package

Random Forests

  • Limitation of a single tree
    • High variance: small changes in data can lead to large changes in predictions
  • Random forests
    • Bootstrap samples from training data
    • Take a random subset of covariates to split on (decorrelate the trees)
    • Tune the number of covariates to split on
  • Implementation: aorsf package

Model Evaluation

  • Brier score
    • Mean squared error between observed survival status and predicted survival probability
    • Inverse probability censoring weighting (IPCW) to account for censoring
    • Integrated Brier score: average Brier score over a time interval
  • ROC AUC
    • Area under the receiver operating characteristic (ROC) curve for survival status
    • IPCW to handle censoring
    • Concordance index: overall AUC over time

tidymodels Workflows

Overview of tidymodels and censored

  • tidymodels: a collection of packages for modeling and machine learning in R
    • Provides a consistent interface for model training, tuning, and evaluation
      • Key package parsnip
    • Supports various model types, including regression, classification, and survival analysis
  • censored: a parsnip extension package for survival data
    • Implements parametric, semiparametric, and tree-based survival models

Data Preparation and Splitting

  • Create a Surv object as response
    • Surv(time, event)
library(tidymodels)
library(censored)
df <- df |>  
  mutate(
    surv_obj = Surv(time, event), # create the Surv object as response variable
    .keep = "unused"              # discard original time and event columns
  )

  • Data splitting

    • initial_split(): splits data into training and testing sets
    df_split <- initial_split(flight_data, prop = 3/4) # default ratio 3:1
df_train <- training(df_split) # obtain training set

Model Specification

  • Model type
    • survival_reg(): parametric AFT models
    • proportional_hazards(penalty = tune()): (regularized) Cox PH models
    • decision_tree(cost_complexity = tune()): decision trees
    • rand_forest(mtry = tune()): random forests
  • Set engine and mode
    • set_engine("survival"): for AFT models
    • set_engine("glmnet"): for Cox PH models
    • set_engine("aorsf"): for random forests
    • set_mode("censored regression"): for survival models
model_spec <- proportional_hazards(penalty = tune()) |>  # regularized Cox model (tune lambda)
  set_engine("glmnet") |>  # set engine to glmnet
  set_mode("censored regression") # set mode to censored regression

Recipe and Workflow

  • Recipe: a series of preprocessing steps for the data
    • recipe(response ~ ., data = df): specify response and predictors
    • step_mutate(): standardize numeric predictors
    • step_dummy(): convert categorical variables to dummy variables
  • Workflow: combines model specification and recipe
    • workflow() |> add_model(model_spec) |> add_recipe(recipe)
# Create a recipe
model_recipe <- recipe(surv_obj ~ ., data = df_train) |> # specify formula
  step_mutate(z1 = z1 / 1000) |>  # standardize z1  
  step_other(z2, z3, threshold = 0.02) |> # group levels with prop < .02 into "other"
  step_dummy(all_nominal_predictors())  # convert categorical variables to dummy variables
# Create a workflow by combining model and recipe
model_wflow <- workflow() |> 
  add_model(model_spec) |>   # add model specification
  add_recipe(model_recipe)   # add recipe

Tune Hyperparameters

  • Cross-validation
    • df_train_folds <- vfold_cv(df_train, v = k): create k-folds on training data (default 10)
    • tune_grid(model_wflow, resamples = df_train_folds): tune hyperparameters using cross-validation
# k-fold cross-validation
df_train_folds <- vfold_cv(df_train, v = 10) # 10-fold cross-validation
# Tune hyperparameters
model_res <- tune_grid(
  model_wflow, 
  resamples = df_train_folds, 
  grid = 10, # number of hyperparameter combinations to try
  metrics = metric_set(brier_survival, brier_survival_integrated,  # specify metrics
                       roc_auc_survival, concordance_survival), 
  eval_time = seq(0, 84, by = 12) # evaluation time points
)

Finalize Workflow

  • Examine validation results
    • collect_metrics(model_res): collect metrics from tuning results
    • show_best(model_res, metric = "brier_survival_integrated", n = 5): show top 5 models based on Brier score
  • Workflow for best model
    • param_best <- select_best(model_res, metric = "brier_survival_integrated"): select best hyperparameters based on Brier score
    • final_wl <- finalize_workflow(model_wflow, param_best): finalize workflow with best hyperparameters
# Extract the best hyperparameters based on Brier score
param_best <- select_best(model_res, metric = "brier_survival_integrated")
# Finalize the workflow with the best hyperparameters
final_wl <- model_wflow |> finalize_workflow(param_best)

Fit Final Model

  • Fit the finalized workflow
    • final_mod <- last_fit(final_wl, split = df_split): fit the finalized workflow on the testing set
    • collect_metrics(final_mod): collect metrics of final model on test data
  • Make predictions
    • predict(final_mod, new_data = new_data, type = "time"): predict survival times on new data
# Fit the finalized workflow on the testing set
final_mod <- last_fit(final_wl, split = df_split)
# Collect metrics of final model on test data
collect_metrics(final_mod) %>% 
  filter(.metric == "brier_survival_integrated")
# Make predictions on new data
new_data <- testing(df_split) |>  slice(1:5) # take first 5 rows of test data
predict(final_mod, new_data = new_data, type = "time")

A Case Study

GBC: Relapse-Free Survival

  • Time to first event
library(tidymodels) # load tidymodels
library(censored)
gbc <- read.table("data/gbc.txt", header = TRUE) # Load GBC dataset
df <- gbc |>  # calculate time to first event (relapse or death)
  group_by(id) |> # group by id
  arrange(time) |> # sort rows by time
  slice(1) |>      # get the first row within each id
  ungroup() |> 
  mutate(
    surv_obj = Surv(time, status), # create the Surv object as response variable
    .after = id, # keep id column after surv_obj
    .keep = "unused" # discard original time and status columns
  )

Data Preparation

  • Analysis dataset
head(df) # show the first few rows of the dataset
# A tibble: 6 × 10
     id   surv_obj hormone   age  meno  size grade nodes  prog estrg
  <int>     <Surv>   <int> <int> <int> <int> <int> <int> <int> <int>
1     1 43.836066        1    38     1    18     3     5   141   105
2     2 46.557377        1    52     1    20     1     1    78    14
3     3 41.934426        1    47     1    30     2     1   422    89
4     4  4.852459+       1    40     1    24     1     3    25    11
5     5 61.081967+       2    64     2    19     2     1    19     9
6     6 63.377049+       2    49     2    56     1     3   356    64
  • Data splitting
set.seed(123) # set seed for reproducibility
gbc_split <- initial_split(df) # split data into training and testing sets
gbc_split 
<Training/Testing/Total>
<514/172/686>

Models to be Trained

  • Regularized Cox model
    • proportional_hazards(penalty = tune())
    • Default: \(\alpha = 1\) (lasso)
    • Tune penalty parameter \(\lambda\)
    • Use glmnet engine for fitting
  • Random forest
    • rand_forest(mtry = tune(), min_n = tune())
    • Tune number of predictors to split on and minimum size of terminal node
    • Use aorsf engine for fitting
# Training data
gbc_train <- training(gbc_split) # obtain training set

Common Recipe

  • Recipe for both models 
gbc_recipe <- recipe(surv_obj ~ ., data = gbc_train) |> # specify formula
  step_mutate(
    grade = factor(grade),
    age40 = as.numeric(age >= 40), # create a binary variable for age >= 40
    prog = prog / 100, # rescale prog
    estrg = estrg / 100 # rescale estrg
  ) |> 
  step_dummy(grade) |> 
  step_rm(id) # remove id
# gbc_recipe # print recipe information

Regularized Cox Model

  • Cox model specification and workflow
# Regularized Cox model specification
cox_spec <- proportional_hazards(penalty = tune()) |>  # tune lambda
  set_engine("glmnet") |>  # set engine to glmnet
  set_mode("censored regression") # set mode to censored regression
cox_spec # print model specification
Proportional Hazards Model Specification (censored regression)

Main Arguments:
  penalty = tune()

Computational engine: glmnet 
# Create a workflow by combining model and recipe
cox_wflow <- workflow() |> 
  add_model(cox_spec) |>   # add model specification
  add_recipe(gbc_recipe)   # add recipe

Model Tuning

  • Cross-validation set-up
    • For both models
set.seed(123) # set seed for reproducibility
gbc_folds <- vfold_cv(gbc_train, v = 10) # 10-fold cross-validation
# Set evaulation metrics
gbc_metrics <- metric_set(brier_survival, brier_survival_integrated, 
                          roc_auc_survival, concordance_survival)
gbc_metrics # evaluation metrics info
A metric set, consisting of:
- `brier_survival()`, a dynamic survival metric               | direction:
minimize
- `brier_survival_integrated()`, a integrated survival metric | direction:
minimize
- `roc_auc_survival()`, a dynamic survival metric             | direction:
maximize
- `concordance_survival()`, a static survival metric          | direction:
maximize
# Set evaluation time points
time_points <- seq(0, 84, by = 12) # evaluation time points

Cox Model Tuning

  • Tune the regularized Cox model
    • Use tune_grid() to perform hyperparameter tuning
    • Evaluate performance using Brier score and ROC AUC
set.seed(123) # set seed for reproducibility
# Tune the regularized Cox model (this will take some time)
cox_res <- tune_grid(
  cox_wflow, 
  resamples = gbc_folds, 
  grid = 10, # number of hyperparameter combinations to try
  metrics = gbc_metrics, # evaluation metrics
  eval_time = time_points, # evaluation time points
  control = control_grid(save_workflow = TRUE) # save workflow
)

Cox Model Tuning Results

  • Plot Brier score as function of \(\log\lambda\)
collect_metrics(cox_res) |>  # collect metrics from tuning results
  filter(.metric == "brier_survival_integrated") |>  # filter for Brier score
  ggplot(aes(log(penalty), mean)) + # plot log-lambda vs Brier score
  geom_line() +  # plot line
  labs(x = "Log-lambda", y = "Overall Brier Score") + # labels
  theme_classic() # classic theme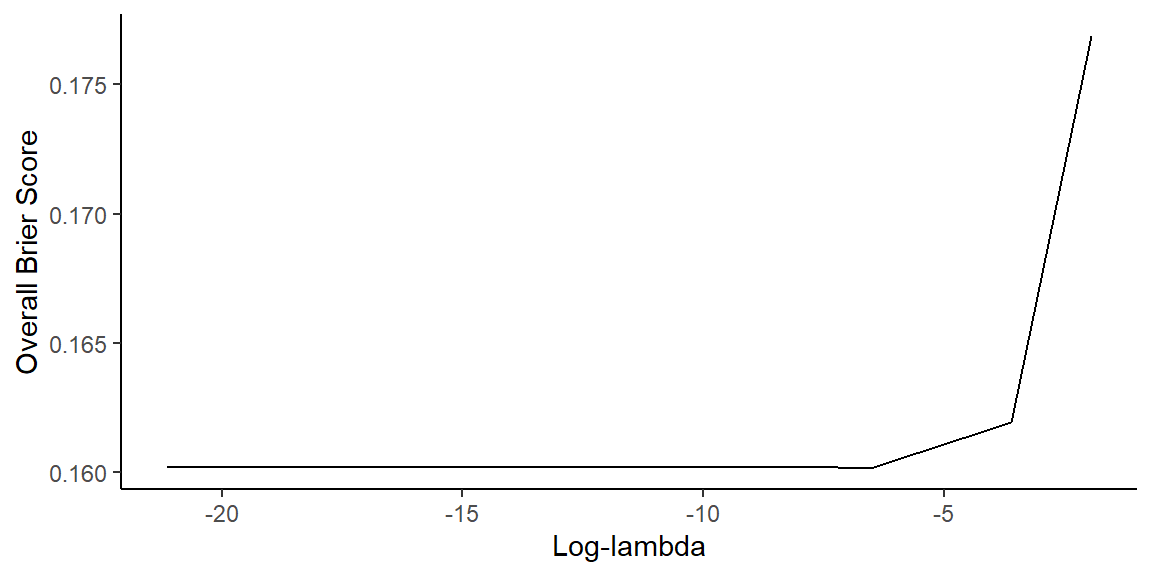

Best Cox Models

  • Show best models

    • Based on Brier score
    show_best(cox_res, metric = "brier_survival_integrated", n = 5) # top 5 models
    # A tibble: 5 × 8
       penalty .metric         .estimator .eval_time  mean     n std_err .config
         <dbl> <chr>           <chr>           <dbl> <dbl> <int>   <dbl> <chr>  
1 0.00147      brier_survival… standard           NA 0.160    10 0.00775 Prepro…
2 0.0000127    brier_survival… standard           NA 0.160    10 0.00775 Prepro…
3 0.0000000105 brier_survival… standard           NA 0.160    10 0.00775 Prepro…
4 0.000754     brier_survival… standard           NA 0.160    10 0.00775 Prepro…
5 0.00000409   brier_survival… standard           NA 0.160    10 0.00775 Prepro…

Random Forest Model

  • Random forest specification and workflow
# Random forest model specification
rf_spec <- rand_forest(mtry = tune(), min_n = tune()) |>  # tune mtry and min_n
  set_engine("aorsf") |>  # set engine to aorsf
  set_mode("censored regression") # set mode to censored regression
rf_spec # print model specification
Random Forest Model Specification (censored regression)

Main Arguments:
  mtry = tune()
  min_n = tune()

Computational engine: aorsf 
# Create a workflow by combining model and recipe
rf_wflow <- workflow() |> 
  add_model(rf_spec) |>   # add model specification
  add_recipe(gbc_recipe)   # add recipe

Random Forest Tuning

  • Tune the random forest model
    • Similar to Cox model tuning
set.seed(123) # set seed for reproducibility
# Tune the random forest model (this will take some time)
rf_res <- tune_grid(
  rf_wflow, 
  resamples = gbc_folds, 
  grid = 10, # number of hyperparameter combinations to try
  metrics = gbc_metrics, # evaluation metrics
  eval_time = time_points # evaluation time points
)

Random Forest Tuning Results

  • View validation results
collect_metrics(rf_res) |> head()   # collect metrics from tuning results
# A tibble: 6 × 9
   mtry min_n .metric         .estimator .eval_time   mean     n std_err .config
  <int> <int> <chr>           <chr>           <dbl>  <dbl> <int>   <dbl> <chr>  
1     3    30 brier_survival  standard            0 0         10 0       Prepro…
2     3    30 roc_auc_surviv… standard            0 0.5       10 0       Prepro…
3     3    30 brier_survival  standard           12 0.0635    10 0.00706 Prepro…
4     3    30 roc_auc_surviv… standard           12 0.827     10 0.0314  Prepro…
5     3    30 brier_survival  standard           24 0.163     10 0.0114  Prepro…
6     3    30 roc_auc_surviv… standard           24 0.747     10 0.0475  Prepro…

Best Random Forest Models

  • Show best models
    • Based on Brier score
show_best(rf_res, metric = "brier_survival_integrated", n = 5) # top 5 models
# A tibble: 5 × 9
   mtry min_n .metric          .estimator .eval_time  mean     n std_err .config
  <int> <int> <chr>            <chr>           <dbl> <dbl> <int>   <dbl> <chr>  
1     6    24 brier_survival_… standard           NA 0.155    10 0.00765 Prepro…
2     5    27 brier_survival_… standard           NA 0.155    10 0.00782 Prepro…
3     4    20 brier_survival_… standard           NA 0.156    10 0.00777 Prepro…
4     9    36 brier_survival_… standard           NA 0.156    10 0.00743 Prepro…
5     2     7 brier_survival_… standard           NA 0.156    10 0.00829 Prepro…
  • Conclusion
    • Best RF model has lower Brier score than best Cox model

Finalize and Fit Best Model

  • Fit final RF model
# Select best RF hyperparameters (mtry, min_n) based on Brier score
param_best <- select_best(rf_res, metric = "brier_survival_integrated") 
param_best # view results
# A tibble: 1 × 3
   mtry min_n .config              
  <int> <int> <chr>                
1     6    24 Preprocessor1_Model07
# Finalize the workflow with the best hyperparameters
rf_final_wflow <- finalize_workflow(rf_wflow, param_best) # finalize workflow
# Fit the finalized workflow on the testing set
set.seed(123) # set seed for reproducibility
final_rf_fit <- last_fit(
  rf_final_wflow, 
  split = gbc_split, # use the original split
  metrics = gbc_metrics, # evaluation metrics
  eval_time = time_points # evaluation time points
)

Test Performance (I)

  • Collect metrics on test data
collect_metrics(final_rf_fit) |> # collect overall performance metrics
  filter(.metric %in% c("concordance_survival", "brier_survival_integrated")) 
# A tibble: 2 × 5
  .metric                   .estimator .eval_time .estimate .config             
  <chr>                     <chr>           <dbl>     <dbl> <chr>               
1 brier_survival_integrated standard           NA     0.237 Preprocessor1_Model1
2 concordance_survival      standard           NA     0.655 Preprocessor1_Model1
# Extract test ROC AUC over time
roc_test <- collect_metrics(final_rf_fit) |>  
  filter(.metric == "roc_auc_survival") |>  # filter for ROC AUC
  rename(mean = .estimate) # rename mean column

Test Performance (II)

  • Plot test ROC AUC over time
roc_test |>  # pass the test ROC AUC data
  ggplot(aes(.eval_time, mean)) +  # plot evaluation time vs mean ROC AUC
  geom_line() + # plot line
  labs(x = "Time (months)", y = "ROC AUC") + # labels
  theme_classic()

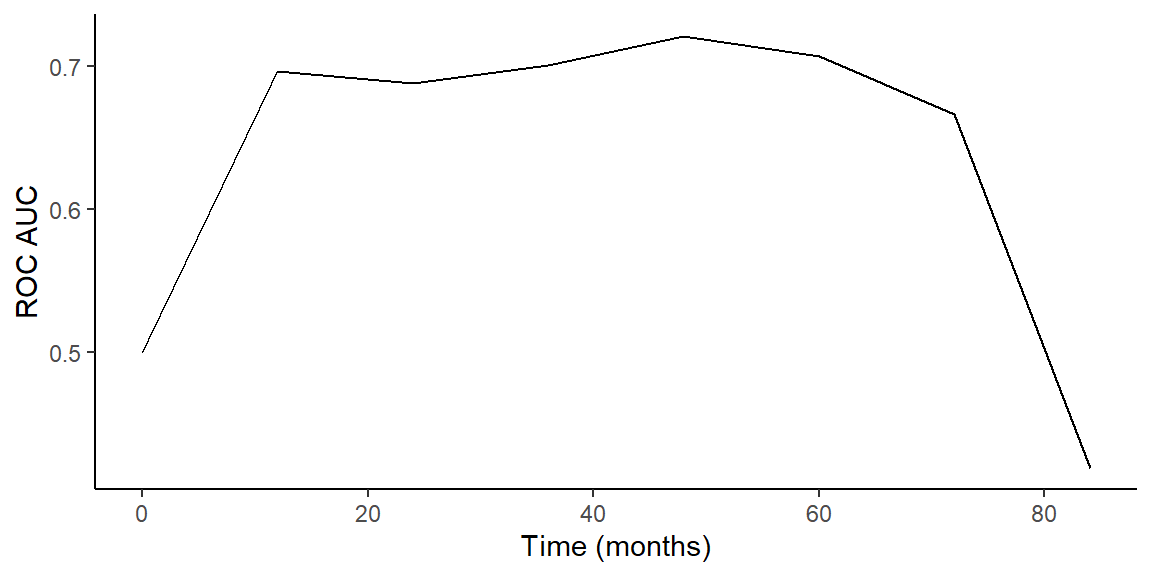
Prediction by Final RF Model

  • Extract the fitted workflow
    • Use extract_workflow() to get the final model
gbc_rf <- extract_workflow(final_rf_fit) # extract the fitted workflow
# Predict on new data
gbc_5 <- testing(gbc_split) |>  slice(1:5) # take first 5 rows of test data
predict(gbc_rf, new_data = gbc_5, type = "time") # predict survival times
# A tibble: 5 × 1
  .pred_time
       <dbl>
1       47.6
2       67.1
3       67.2
4       36.1
5       49.7

Cox Model Exercise (I)

  • Task: extract the best Cox model from cox_res and fit it to test data
Solution 
# Select best Cox hyperparameters (penalty) based on Brier score
param_best_cox <- select_best(cox_res, metric = "brier_survival_integrated")
# Finalize the workflow with the best hyperparameters
cox_final_wflow <- finalize_workflow(cox_wflow, param_best_cox) # finalize workflow
# Fit finalized workflow on the testing set
final_cox_fit <- last_fit(
  cox_final_wflow, 
  split = gbc_split, # use the original split
  metrics = gbc_metrics, # evaluation metrics
  eval_time = time_points # evaluation time points
)
# Collect metrics on test data
collect_metrics(final_cox_fit) |> # collect overall performance metrics
  filter(.metric %in% c("concordance_survival", "brier_survival_integrated"))

Cox Model Exercise (II)

Solution - continued 
# Extract test ROC AUC over time
roc_test_cox <- collect_metrics(final_cox_fit) |>  
  filter(.metric == "roc_auc_survival") |>  # filter for ROC AUC
  rename(mean = .estimate) # rename mean column
roc_test_cox |>  # pass the test ROC AUC data
  ggplot(aes(.eval_time, mean)) +  # plot evaluation time vs mean ROC AUC
  geom_line() + # plot line
  labs(x = "Time (months)", y = "ROC AUC") + # labels
  theme_classic()

# Predict on new data
# Extract fitted workflow
gbc_cox <- extract_workflow(final_cox_fit) # extract the fitted workflow
gbc_5 <- testing(gbc_split) |>  slice(1:5) # take first 5 rows of test data
predict(gbc_cox, new_data = gbc_5, type = "time") # predict survival times

Cox Model Exercise (III)

  • Task: find the parameter estimates of final Cox model
    • Hint: use tidy() function from broom package
Solution 
tidy(gbc_cox) # tidy the coefficients
# # A tibble: 10 × 3
#    term     estimate penalty
#    <chr>       <dbl>   <dbl>
#  1 hormone  -0.227   0.00147
#  2 age       0.00908 0.00147
#  3 meno     -0.00736 0.00147
#  4 size      0.0127  0.00147
#  5 nodes     0.0411  0.00147
#  6 prog     -0.270   0.00147
#  7 estrg     0.00771 0.00147
#  8 age40    -0.540   0.00147
#  9 grade_X2  0.573   0.00147
# 10 grade_X3  0.624   0.00147

Survival Tree Exercise

  • Task: fit a survival tree model to the GBC data
    • Use decision_tree() with set_engine("rpart")
    • Tune complexity parameter cost_complexity using tune()
    • Use the same recipe as for Cox and RF models
    • Evaluate performance using Brier score and ROC AUC

Summary

Key Takeaways

  • Machine learning: powerful tools for survival analysis with many covariates
    • Regularized Cox regression, survival trees, and random forests
  • tidymodels: a consistent interface for modeling and machine learning
    • parsnip for model specification and tuning
    • censored packages for survival data
    • Model evaluation: Brier score and ROC AUC for survival models