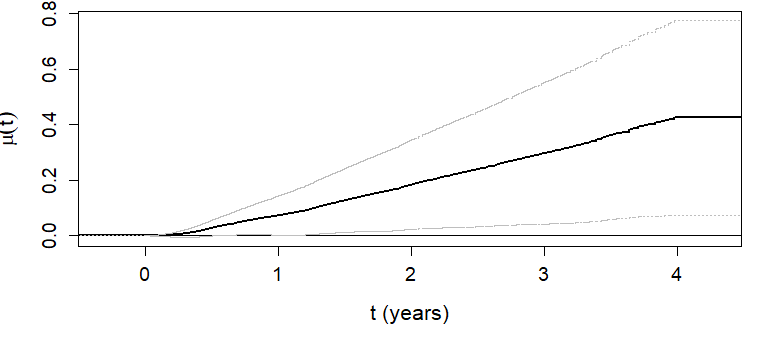Restricted mean time in favor of treatment

An estimand for hierarchical composite endpoints

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

———————————————————————————————

Statistics and Biostatistics seminar series (Oct 22, 2024)

Main paper - https://doi.org/10.1111/biom.13570

Outline

  • Background

  • Approach

    • Estimand (w. decomposition)
    • Estimation & inference
    • Sample size calculation
    • R-package rmt

  • Application

    • HF-ACTION: a CV trial
    • Analysis & results

  • Conclusion

\[ \def\a{{(a)}} \def\b{{(1-a)}} \def\t{{(1)}} \def\c{{(0)}} \def\d{{\rm d}} \def\T{{\rm T}} \]

Introduction

Motivating Examples

  • Colon cancer trial
    • Levamisole + fluorouracil (\(n=304\)) vs control (\(n=315\))
    • Relapse-free survival
      • 258 (89%) deaths ignored
  • HF-ACTION trial
    • Exercise training (\(n=205\)) vs usual care (\(n=221\))
    • Hospitalization-free survival
      • 82 (88%) deaths + 707 (69%) hospitalizations ignored

More Generally

  • Complex patient outcomes
    • Multistate process \(Y(t)\in\{0, 1,\ldots, K,\infty\}\) (Cook & Lawless, 2018)
    • Traditional composite endpoint
      • Time to first event \(\tilde T =\inf\{t: Y(t) > 0\}\) \(\to\) event-free survival
    • Hierarchical composite endpoint
      • Death (> metastasis) > relapse
      • Death > number of hospitalizations

Model-free Effect Size

  • Two-sample comparison
    • \(Y^\a(t)\): patient in group \(a\) (\(a=1\): treatment; \(0\): control)
  • Estimand for traditional composite
    • Event-free survival rate: \(\tilde S^\a(t)=P(\tilde T^\a >t)\)
    • Restricted mean event-free survival time (RMEST) \[ \mu_E^\a(\tau) = E\{\min(\tilde T^\a ,\tau)\}=\int_0^\tau \tilde S^\a(t)\d t \]
      • A variation of the RMST
    • Net event-free survival time attributable to treatment \[ \mu_E(\tau) = \mu_E^\t(\tau) - \mu_E^\c(\tau) \]

Hierarchical Composite

  • Win ratio (Pocock et al., 2012)
    • Standard estimand involves censoring, but fixable by time restriction (Mao, 2024)
    • Win probability \[ w^\a(t) = {\mbox{probability group $a$ wins by time $t$}} \]
    • Restricted WR: \(w^\t(\tau)/w^\c(\tau)\)
    • Restricted proportion in favor (PIF): \(w^\t(\tau) - w^\c(\tau)\)
  • Time difference?
    • Win-loss: proportion \(\to\) average time

Estimand Construction (& Deconstruction)

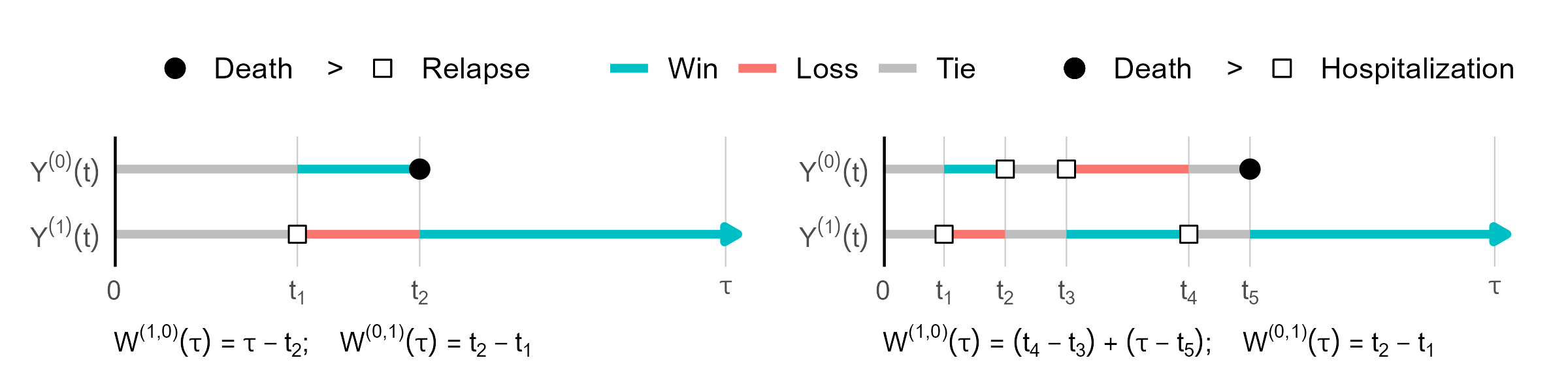
Time on a Win or Loss

  • For a given pair
    • \(Y^\t(t)\) vs \(Y^\c(t)\) over \([0, \tau]\)
    • Win/loss time \(=\) total time in a lower/higher-tiered state \[ W^{(a, 1-a)}(\tau)=\int_0^\tau I\{Y^\a(t)<Y^\b(t)\}\d t \]
      • Scan \([0, \tau]\) to get \(W^{(1, 0)}(\tau)\) & \(W^{(0, 1)}(\tau)\)

Net Average Win Time

  • Etimand of treatment effect
    • Restricted mean time in favor (RMT-IF) of treatment (Mao, 2023a) \[ \mu(\tau) = E\{W^{(1, 0)}(\tau) - W^{(0, 1)}(\tau)\} \]
      • Net average time in a more favorable state due to treatment
    • Component-wise contribution \[\begin{align} \mu(\tau) = \sum_{k=1}^{K,\infty} \mu_k(\tau) := \sum_{k=1}^{K,\infty} E\left\{W_k^{(1, 0)}(\tau) - W_k^{(0, 1)}(\tau)\right\} \end{align}\]
      • \(W_k^{(a, 1-a)}(\tau)=\int_0^\tau I\{Y^\a(t)<Y^\b(t) = k\}\d t\): time won on state \(k\) (being in a better state)
      • \(\mu_k(\tau)\): net average time won on state \(k\)
        • \(\mu_1(\tau)\): net average time pre-relapse (remission) time
        • \(\mu_2(\tau)\): net average time pre-metastasis (remission/relapse) time
        • \(\mu_\infty(\tau)\): \(=\) net average survival (remission/relapse/metastasis) time \(=\) difference in RMST

Simplify for Progressive Processes

  • Progressive process
    • Definition: \(Y^\a(t)\leq Y^\a(s)\) for all \(0\leq t\leq s\)
      • Only going forward (all earlier examples)
    • Transition time \(T_k^\a\): time to transition to a state \(\geq k\)
      • \(T_1^\a\): time to relapse/metastasis/death
      • \(T_2^\a\): time to metastasis/death
      • \(T_\infty^\a=D^\a\): time to death
    • Reformulation: \(Y^\a(\cdot)\equiv \big\{0\leq T_1^\a\leq\cdots\leq T_K^\a\leq T_\infty^\a\big\}\)
      • A progressive process \(\Longleftrightarrow\) a sequence of time marks for transitions

Delve into Estimand

  • Average win time on state \(k\)
    • Re-expression with \(S_k^\a(t)=P\{T_k^\a > t\}\) \[\begin{align} E\{W_k^{(a, 1-a)}(\tau)\}&=E\left\{\int_0^\tau I\{Y^\a(t)<Y^\b(t) = k\}\d t\right\}\\ &=\int_0^\tau P\{Y^\a(t)< k\}P\{Y^\b(t) = k\}\d t\\ &=\int_0^\tau P\{T_k^\a > t\}P\{T_k^\b \leq t < T_{k+1}^\b \}\d t\\ &=\int_0^\tau S_k^\a(t)\left\{S_{k+1}^\b(t) - S_k^\b(t)\right\}\d t\\ \end{align}\]
    • Net average win time \[\mu_k(\tau)=E\{W_k^{(1, 0)}(\tau)\}-E\{W_k^{(0, 1)}(\tau)\}= \int_0^\tau \left\{S_k^\t(t)S_{k+1}^\c(t) - S_k^\c(t)S_{k+1}^\t(t)\right\}\d t\]

Estimation and Inference

Observed Data & Estimation

  • Censored observations \[ (X_k^\a, \delta_k^\a),\,\,\, k =1,\ldots, K, \infty \]
    • \(X_k^\a = \min(T_k^\a, C^\a)\); \(\delta_k^\a = I(T_k^\a \leq C^\a)\); \(C^\a=\) censoring time
    • Kaplan–Meier estimator \(\hat S_k^\a(t)\)
  • Estimation
    • Plug-in KM estimator \[ \hat\mu_k(\tau)= \int_0^\tau \left\{\hat S_k^\t(t)\hat S_{k+1}^\c(t) - \hat S_k^\c(t)\hat S_{k+1}^\t(t)\right\}\d t \]
    • Robust variance estimator

Hypothesis Testing

  • Test of overall effect
    • \(\chi_1^2\) test based on \(\hat\mu(\tau)=\sum_{k=1}^{K,\infty}\hat\mu_k(\tau)\) for \[ H_0: \mu(\tau)= 0 \]
  • Joint test on components
    • \(\chi_{K+1}^2\) test based on \(\hat\mu_1(\tau),\ldots,\hat\mu_K(\tau),\hat\mu_\infty(\tau)\) \[ H_0: \mu_1(\tau)=\cdots=\mu_K(\tau)=\mu_\infty(\tau) \]
      • Or individual components for secondary analyses
    • Further decomposition: \(\mu_k(\tau) = \sum_{j=0}^{k-1}\mu_{jk}(\tau)\) (Mao & Wang, 2024)
      • \(\mu_2(\tau)=\mu_{02}(\tau) + \mu_{12}(\tau)\): net pre-metastasis time in remission or after relapse
      • \(\mu_\infty(\tau)=\mu_{0,\infty}(\tau), \mu_{1,\infty}(\tau), \mu_{2,\infty}(\tau)\): net survival time in different states

Sample Size Calculation

  • Semi-competing risks (illness-death model)
    • Gumbel–Hougaard copula (Mao, 2023b)
    • Input parameters
      • Baseline: Hazards for death & relapse, association parameter b/t them
      • Effect sizes: Component-wise hazard ratios
  • Recurrent events with death
    • Homogeneous Markov model (Mao, 2023c)
    • Input parameters
      • Baseline: Intensities for another hospitalization or death, having had \(k-1\) hospitalizations \((k=1,2,\ldots)\)
      • Effect sizes: Intensity (risk) ratios for all transitions

Software: rmt::rmtfit() (I)

  • Input data format (long)
    • Standard multistate
      • status = k for entry into state \(k\), K+1 for death, 0 for censoring
    • Recurrent events with death
      • status = 1 for nonfatal event, 2 for death, 0 for censoring
head(hfaction)
#>       patid       time status trt_ab age60
#>  HFACT00001 0.60506502      1      0     1
#>  HFACT00001 1.04859685      0      0     1
#>  HFACT00002 0.06297057      1      0     1
#>  HFACT00002 0.35865845      1      0     1
#>  HFACT00002 0.39698836      1      0     1
#>  HFACT00002 3.83299110      0      0     1
#>  ...

Software: rmt::rmtfit() (II)

  • Basic syntax
library(rmt)
# trt: binary treatment
obj <- rmtfit(id, time, status, trt, 
              type = c("multistate", "recurrent"))
  • Output: a list of class rmtfit
    • obj$t: \(t\); obj$mu: a matrix of \((K+2)\) rows, \(\hat\mu_k(t)\) in \(k\)th row, \(\hat\mu(t)\) in last; obj$var: variances of point estimates in mu
    • summary(obj, tau) for summary results on \(\mu(\tau)\) (tau: \(\tau\))
    • plot(obj) to plot \(\hat\mu(t)\) against \(t\)

Application

Example: HF-ACTION

  • Exercise training vs usual care
Table 1: Descriptive statistics for a high-risk subgroup (n=426) in HF-ACTION trial.
Usual care (N = 221) Exercise training (N = 205)
Age ≤ 60 years 122 (55.2%) 128 (62.4%)
> 60 years 99 (44.8%) 77 (37.6%)
Follow-up (months) 28.6 (18.4, 39.3) 27.6 (19, 40.2)
Death 57 (25.8%) 36 (17.6%)
Hospitalizations 0 51 (23.1%) 60 (29.3%)
1-3 114 (51.6%) 102 (49.8%)
4-10 49 (22.2%) 39 (19%)
>10 7 (3.2%) 4 (2%)

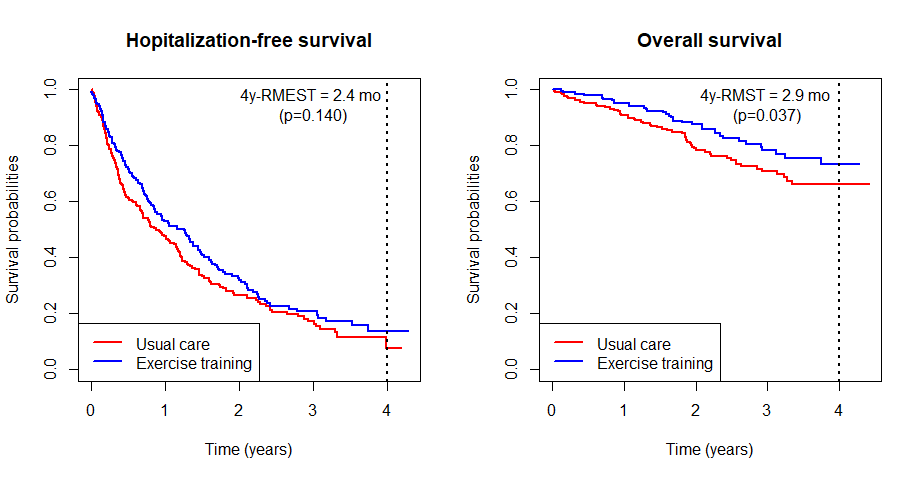
Standard Analyses

  • Traditional composite and overall survival

R-Code

library(rmt)
head(hfaction)
#>       patid       time status trt_ab age60
#>  HFACT00001 0.60506502      1      0     1
#>  HFACT00001 1.04859685      0      0     1
#> ...
# fit RMT-IF
obj <- rmtfit(hfaction$patid, hfaction$time, hfaction$status, hfaction$trt, 
              type = "recurrent")
summary(obj, Kmax = 4, tau = 3.97) ## combine recurrent events >= 4
# Restricted mean time in favor of group "1" by time tau = 3.97:
#   Estimate    Std.Err Z value Pr(>|z|)    
# Event 1   0.0140515  0.0498836  0.2817 0.778184    
# Event 2   0.0358028  0.0499618  0.7166 0.473619    
# Event 3   0.1385287  0.0409533  3.3826 0.000718 ***
# Event 4+ -0.0064731  0.0600813 -0.1077 0.914203    
# Survival  0.2384169  0.1143484  2.0850 0.037069 *  
# Overall   0.4203268  0.1777363  2.3649 0.018035 *

Graphics

  • \(\hat\mu(t)\) as a function of \(t\)

    • Overall RMT-IF becomes significant after 1 year (see lower CL)
    plot(obj, conf = TRUE, conf.col = "gray", lwd = 2, xlab = "t (years)",
     ylab = "expression(mu(t))", main = "")

Inference Results

  • 4-year RMT-IF of exercise training
    • Training on average gains 5.1 months (\(P\)=0.018) in favorable state
    Estimate SE P-value
    Hopitalization 2.18 1.22 0.073
    1 0.17 0.60 0.778
    2 0.43 0.60 0.474
    3 1.66 0.49 <0.001
    4+ -0.08 0.72 0.914
    Death 2.86 1.37 0.037
    Overall 5.04 2.13 0.018
    • 2.9 months net survival \(+\) 2.2 months net time with fewer hospitalizations (little effect on 1st)

Favorability Plot

  • 4-year average win-loss times

Summary and Discussion

Summary

  • RMT-IF
    • A model-free estimand to measure treatment effect on hierarchical composite endpoints
    • Net average win time \(=\) Average win \(-\) loss time
      • \(\sum_k\) (Net average win time on \(k\)th component)
    • R-package: rmt
      • obj <- rmtfit(id, time, status, trt, type = c("multistate", "recurrent"))
      • summary(obj, tau)
      • plot(obj)

Discussion

  • Standard win-loss measures
    • Longer survivor wins categorically (on patient-level)
  • RMT-IF

    • Quantitative win-loss times (on patient-time-level)

    • Loss on nonfatal event can (more than) offset win on survival

      • Disregard win/loss time on nonfatal event in presence of death?

Future Topics

  • Covariate adjustment
    • Conditional estimand \(\to\) regression modeling
    • Marginal estimand \(\to\) Augmentation under working regression model (locally efficient estimation)
  • Intercurrent event
    • Treatment non-response/toxicity/discontinuation (ICH, 2020)
      • “occurring after treatment initiation that affect either the interpretation or the existence of the measurements associated with the clinical question of interest”
    • How to measure win/loss time afterward?

Acknowledgments

References

Cook, R. J., & Lawless, J. F. (2018). Multistate models for the analysis of life history data. Chapman; Hall/CRC. https://doi.org/10.1201/9781315119731
Dong, G., Huang, B., Wang, D., Verbeeck, J., Wang, J., & Hoaglin, D. C. (2021). Adjusting win statistics for dependent censoring. Pharmaceutical Statistics, 20(3), 440–450. https://doi.org/10.1002/pst.2086
Dong, G., Mao, L., Huang, B., Gamalo-Siebers, M., Wang, J., Yu, G., & Hoaglin, D. C. (2020b). The inverse-probability-of-censoring weighting (IPCW) adjusted win ratio statistic: an unbiased estimator in the presence of independent censoring. Journal of Biopharmaceutical Statistics, 30(5), 882–899. https://doi.org/10.1080/10543406.2020.1757692
ICH. (2020). ICH E9 (R1) addendum on estimands and sensitivity analysis in clinical trials to the guideline on statistical principles for clinical trials, step 5. London: European Medicines Evaluation Agency.
Mao, L. (2023a). On restricted mean time in favor of treatment. Biometrics, 79(1), 61–72. https://doi.org/10.1111/biom.13570
Mao, L. (2023b). Power and Sample Size Calculations for the Restricted Mean Time Analysis of Prioritized Composite Endpoints. Statistics in Biopharmaceutical Research, 15(3), 540–548. https://doi.org/10.1080/19466315.2022.2110936
Mao, L. (2023c). Study Design for Restricted Mean Time Analysis of Recurrent Events and Death. Biometrics, 79(4), 3701–3714. https://doi.org/10.1111/biom.13923
Mao, L. (2024). Defining estimand for the win ratio: Separate the true effect from censoring. Clinical Trials, 10.1177/17407745241259356.
Mao, L., & Wang, T. (2024). Dissecting the restricted mean time in favor of treatment. Journal of Biopharmaceutical Statistics, 34(1), 111–126. https://doi.org/10.1080/10543406.2023.2210658
Pocock, S. J., Ariti, C. A., Collier, T. J., & Wang, D. (2012). The win ratio: a new approach to the analysis of composite endpoints in clinical trials based on clinical priorities. European Heart Journal, 33(2), 176–182. https://doi.org/10.1093/eurheartj/ehr352