Applied Survival Analysis

Chapter 9 - Recurrent Events

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Intensity and rate/mean functions

  2. Cox-type models for recurrent events

  3. Analysis of the Chronic Granulomatous Disease Study

  4. Multivariate approaches to recurrent events

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Intensity and Marginal Rate

Recurrent Events

  • Repeated occurrences of an adverse event

    • Infections (CGD)
    • Tumor occurrences
    • Hospitalizations
    • Episodes of CV events: chest pain (angina), irregular heart beat (tachycardia)

  • Naive approach: time to first event

  • Recurrent event process

    • Statistically more efficient
    • Fuller picture of patient experience

Outcome Data

  • Target of inference
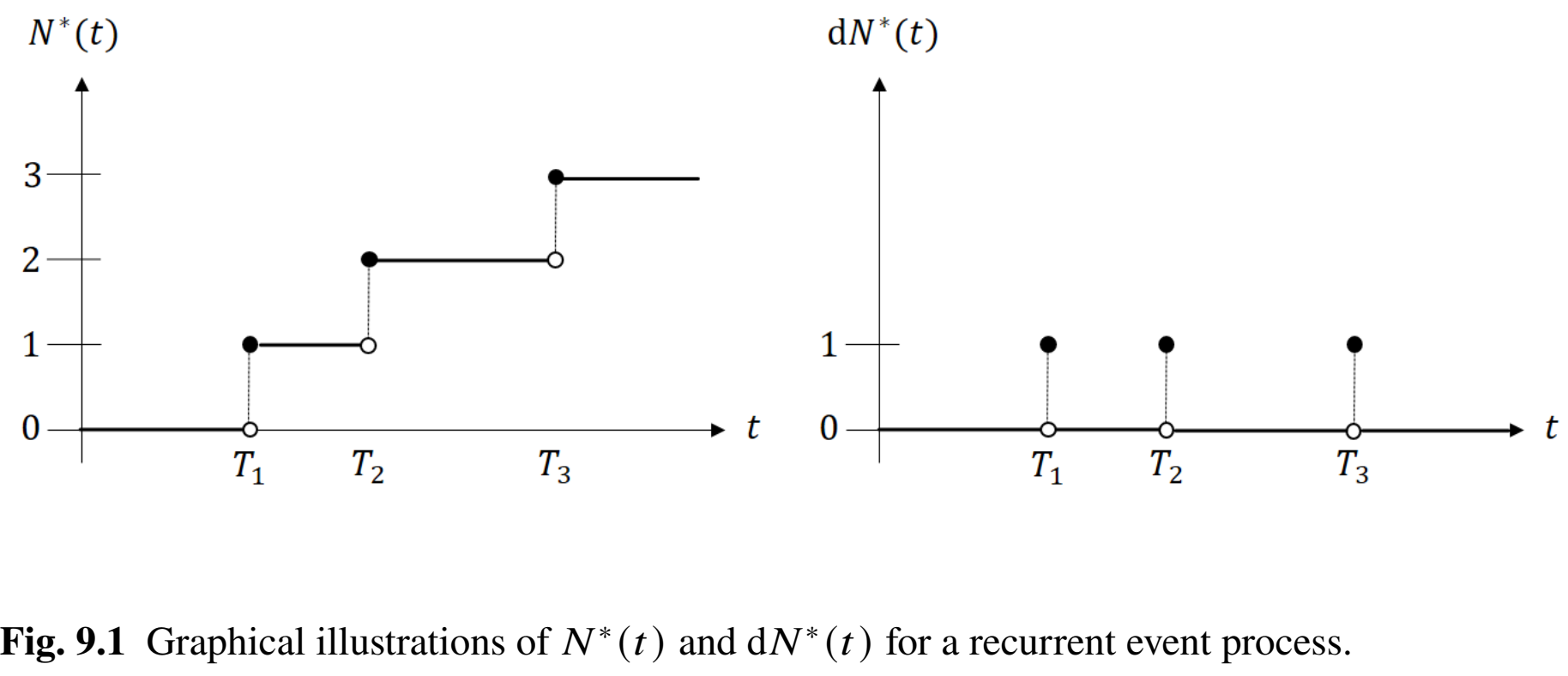
    • \(N^*(t)\): number of recurrent events by \(t\)
      • \(N^*(t)=\sum_{k=1}^\infty I(T_k\leq t)\)
      • \(T_1<T_2<\cdots\): recurrent event times

Intensity Function

  • Modeling recurrent events
    • Intensity: conditional incidence given history
    • Rate: marginal incidence across population
  • Intensity: Current risk given event history \[\begin{equation}\label{eq:rec:intensity} \ell\{t\mid \overline{N}^*(t-)\}\dd t=E\{\dd N^*(t)\mid \overline{N}^*(t-)\} \end{equation}\]
    • \(\overline{N}^*(t-)=\{N^*(u):0\leq u < t\}\)
    • Univariate case \[ \ell\{t\mid \overline{N}^*(t-)\}=I(T\geq t)\lambda(t)\dd t \]
      • Intensity \(=\) an extension of hazard

Example: Poisson Process

  • Independent events \[\begin{equation}\label{eq:rec:poisson} E\{\dd N^*(t)\mid \overline{N}^*(t-)\}=\ell(t) \end{equation}\]
    • Current risk \(\ell(t)\) independent of past
      • Homogeneous Poisson: \(\ell(t) = \lambda\)
    • Generally unrealistic in medical applications
      • More previous events \(\to\) higher current risk
  • Poisson properties
    • \(N^*(t_{j}) - N^*(t_{j-1})\), number of events in \((t_{j-1}, t_{j}]\) \((j=1, 2, \ldots)\), are mutually independent for \(0=t_0< t_1 < t_2 <\cdots\),
    • \(N^*(t_{j}) - N^*(t_{j-1})\) follows Poisson distribution with mean \(\int_{t_{j-1}}^{t_j}\ell(u)\dd u\).

Rate Function

  • Rate: Marginal incidence \[\begin{equation}\label{eq:rec:rate} r(t)\dd t=E\{\dd N^*(t)\} \end{equation}\]

  • Mean: Average number of events \[\begin{equation}\label{eq:rec:mean} \mu(t)=E\{N^*(t)\}=\int_0^t r(u)\dd u \end{equation}\]

  • Rate vs intensity \[ r(t)=E\left[\ell\{t\mid \overline{N}^*(t-)\}\right] \]

    • Poisson process: \(r(t)=\ell(t)\)

One-Sample Estimation of Mean

  • Observed data \[\begin{equation}\label{eq:rec:obs} \{N_i(\cdot), C_i, Z_i\},\hspace{10mm}i=1,\ldots, n \end{equation}\]
    • \(N(t)=N^*(t\wedge C)\); \(C\): independent censoring time
    • No terminal event like death \(\to\) \(C\) always observed
  • Nelsen-Aalen-type estimator for mean \[ \hat\mu(t)=\int_0^t\frac{\sum_{i=1}^n\dd N_i(u)}{\sum_{i=1}^n I(C_i\geq u)} \]
    • \(\hat\mu(t)\to \int_0^t\frac{E\{\dd N(u)\}}{\pr(C\geq u)}=\int_0^t\frac{\pr(C\geq u)E\{\dd N^*(u)\}}{\pr(C\geq u)}=\int_0^t r(u)\dd u=\mu(t)\)

Proportional Intensity/Rates Models

Proportional Intensity (Andersen-Gill)

  • Three classes of models (handle correlations)
    • Proportional intensity (by time-varying covariates)
    • Shared frailty (by subject-specific frailty)
    • Proportional rates (by robust inference)
  • Proportional intensity (Andersen & Gill, 1982) \[\begin{equation}\label{eq:rec:AG_model} E\{\dd N^*(t)\mid \overline N^*(t-), \overline Z(t)\}=\exp\left\{\beta^\T Z(t)\right\}\dd\mu_0(t) \end{equation}\]
    • \(\beta\): log-intensity (risk) ratio
    • Dependence on past events fully explained by \(Z(t)\) (modulated Poisson)
      • Define \(Z(t)\) to summarize \(\overline N^*(t-)\), e.g., \(N^*(t-)\): number of past events
      • Complicates causal interpretation in randomized trials

Andersen-Gill: Cox Extension

  • Estimation and inference
    • Same as Cox model with (internal) time-varying covariates
    • Partial-likelihood score \[\begin{equation}\label{eq:rec:score} U_n(\beta)=n^{-1}\sum_{i=1}^n\int_0^\infty \left\{Z_i(t)- \frac{\sum_{j=1}^n I(C_j\geq t)Z_j(t)\exp\{\beta^\T Z_j(t)\}}{\sum_{j=1}^n I(C_j\geq t)\exp\{\beta^\T Z_j(t)\}} \right\}\dd N_i(t) \end{equation}\]
      • Full martingale properties
    • Breslow estimator \[\begin{equation}\label{eq:rec:breslow} \hat\mu_0(t)=\int_0^t\frac{\sum_{i=1}^n\dd N_i(u)}{\sum_{i=1}^n I(C_i\geq u)\exp\left\{\hat\beta^\T Z_i(u)\right\}} \end{equation}\]

Shared-Frailty Proportional Intensity

  • Frailty-conditioned intensity \[\begin{equation}\label{eq:rec:frailty_model} E\{\dd N^*(t)\mid \xi, \overline N^*(t-), \overline Z(t)\}=\xi\exp\{\beta^\T Z(t)\}\dd\mu_0(t) \end{equation}\]
    • \(\xi\): subject-specific frailty to capture within-subject correlation
    • \(Z(t)\): no need to capture elements of \(\overline N^*(t-)\)
    • \(\beta\): subject-level log-intensity (risk) ratio
  • Estimation and inference
    • EM algorithm treating \(\xi\) as missing data
    • M-step: weighted partial-likelihood and Breslow estimator

Marginal Proportional Rates (LWYY)

  • Proportion rates (Lin, Wei, Yang & Ying, 2000; LWYY) \[\begin{equation}\label{eq:rec:rate_pr} E\{\dd N^*(t)\mid \overline Z(t)\}=\exp\{\beta^\T Z(t)\}\dd\mu_0(t) \end{equation}\]
    • Modeling marginal rate rather than intensity
    • Baseline \(Z\) \(\to\) proportional means model \[\begin{equation}\label{eq:rec:rate_pm} E\{N^*(t)\mid Z\}=\exp(\beta^\T Z)\mu_0(t) \end{equation}\]
      • \(Z = 1, 0\): treated experience \(\exp(\beta)\) as many events as untreated
  • Estimation and inference
    • Partial-likelihood score as estimating function (same estimates as AG)
    • Robust (sandwich) variance (different \(\se\) than AG)

Software: survival::coxph() (I)

  • Input data format
cgd
# id tstart tstop status   treat    sex age height weight   inherit 
#   1      0   219      1  rIFN-g female  12  147.0   62.0 autosomal
#   1    219   373      1  rIFN-g female  12  147.0   62.0 autosomal
#   1    373   414      0  rIFN-g female  12  147.0   62.0 autosomal
#   2      0     8      1 placebo   male  15  159.0   47.5 autosomal
#...
  • Proportional intensity (Andersen-Gill)
    • (start, stop): time period between previous and current events
    • No need for subject id as correlation presumably captured by covariates
coxph(Surv(start, stop, status) ~ covariates)

Software: survival::coxph() (II)

  • Shared-frailty proportional intensity
    • Subject id for frailty
# Gamma frailty
coxph(Surv(start, stop, status) ~ covariates + 
        frailty(id, distribution = "gamma"))
  • Proportional rates/means (LWYY)
    • Subject id for empirical evaluation of clustering
    • Use se2 in results for robust standard error
coxph(Surv(start, stop, status) ~ covariates + cluster(id))

Chronic Granulomatous Disease Study

Study Background

  • Study information
    • Population: a placebo-controlled randomized trial on 128 Chronic Granulomatous Disease (CGD) patients
    • Aim: evaluate effect of gamma interferon on incidence of repeated CGD infections
    • Baseline risk factors
      • treatment (treat; rIFN-g vs placebo)
      • sex (sex)
      • age (age; years)
      • pattern of inheritance (inherit; autosomal recessive or X-linked)
      • use of steroids (steroids; Yes/No)
      • use of prophylactic antibiotics (propylac; Yes/No)

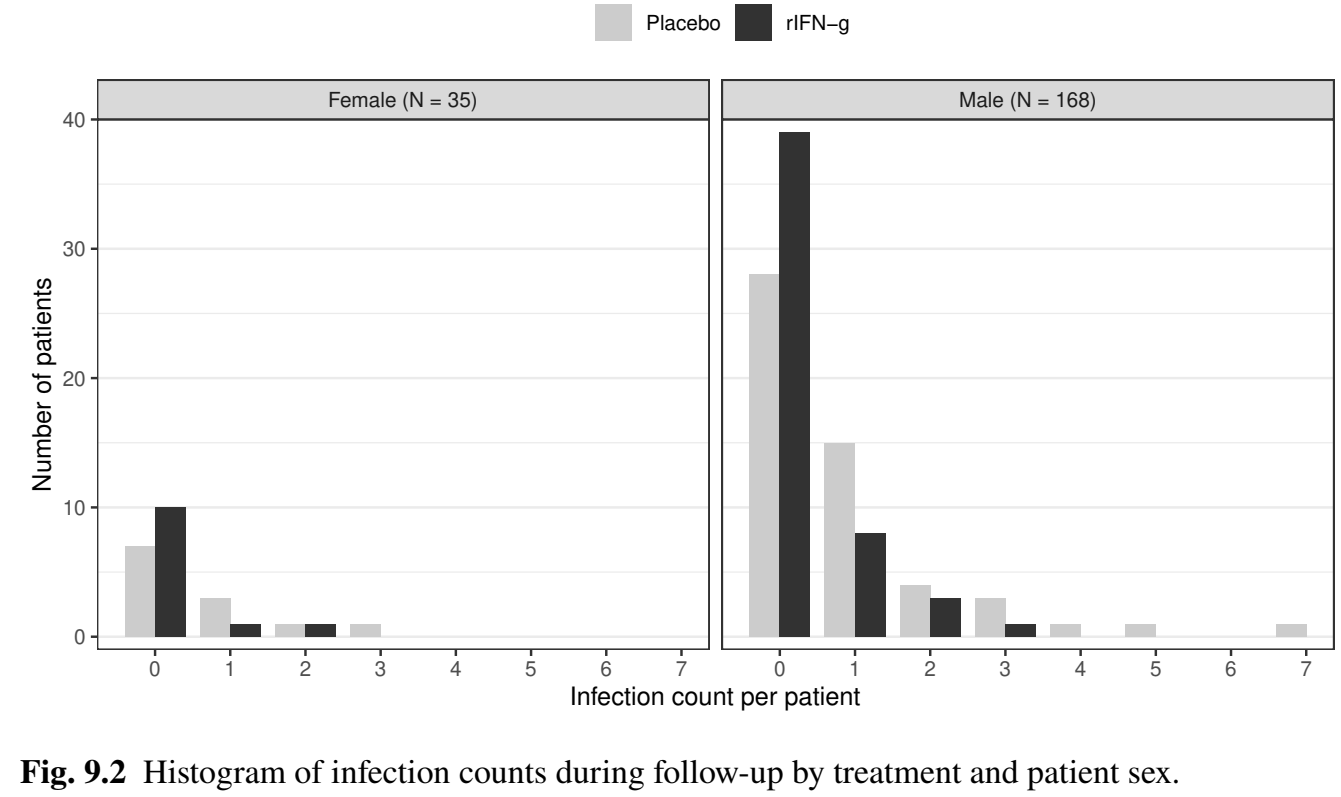
Regression Results (I)

  • Fit three multiplicative models
# Andersen-Gill model
obj.AG <- coxph(Surv(tstart, tstop, status) ~ treat + sex + age + 
                  inherit + steroids + propylac, data = cgd)
# Frailty model
obj.frail <- coxph(Surv(tstart, tstop, status) ~ treat + sex + age + 
                     inherit + steroids + propylac + 
                     frailty(id, distribution = "gamma"), data = cgd)
# proportional mean model (LWYY) - recommended
obj.pm <- coxph(Surv(tstart, tstop, status) ~ treat + sex + age + 
                  inherit + steroids + propylac + cluster(id), data = cgd)
summary(obj.pm)
#                 coef exp(coef) se(coef) robust se      z Pr(>|z|)    
# treatrIFN-g -1.05140   0.34945  0.26500   0.31031 -3.388 0.000703 ***
# sexmale      0.72832   2.07159  0.39044   0.43676  1.668 0.095405 .  
# ...

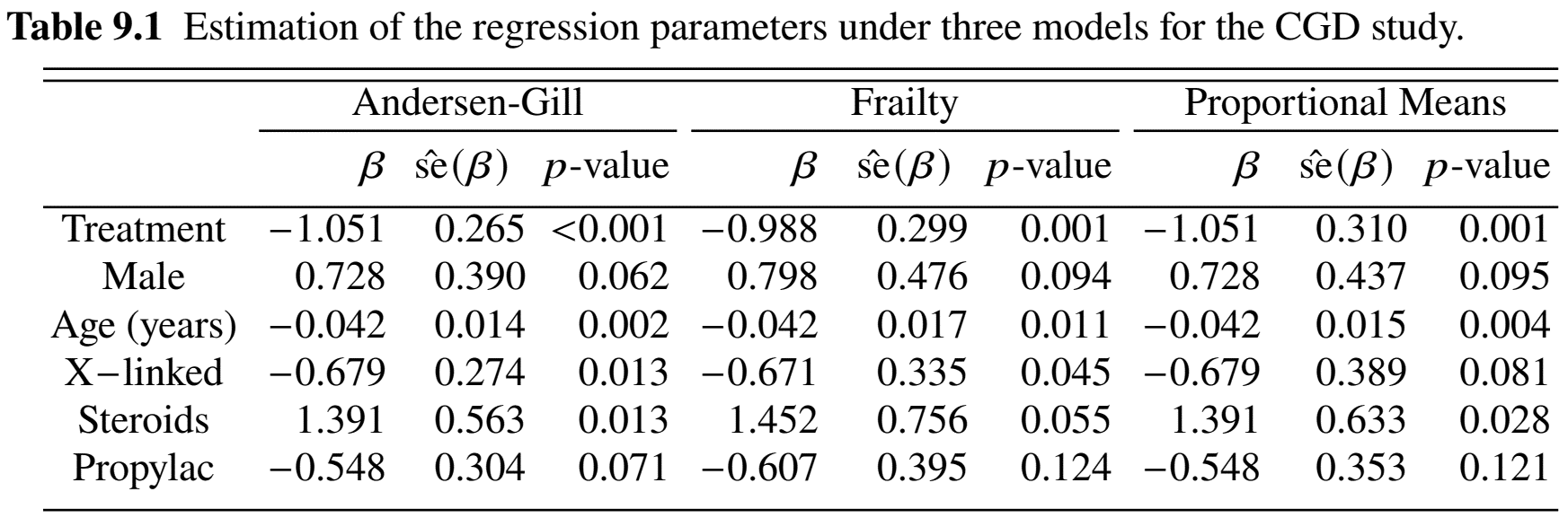
Regression Results (II)

  • LWYY (recommended)
    • patients treated by gamma interferon on average experience \(\exp(-1.051) = 35.0\%\) as many infections as those taking placebo (\(p\)-value 0.001)

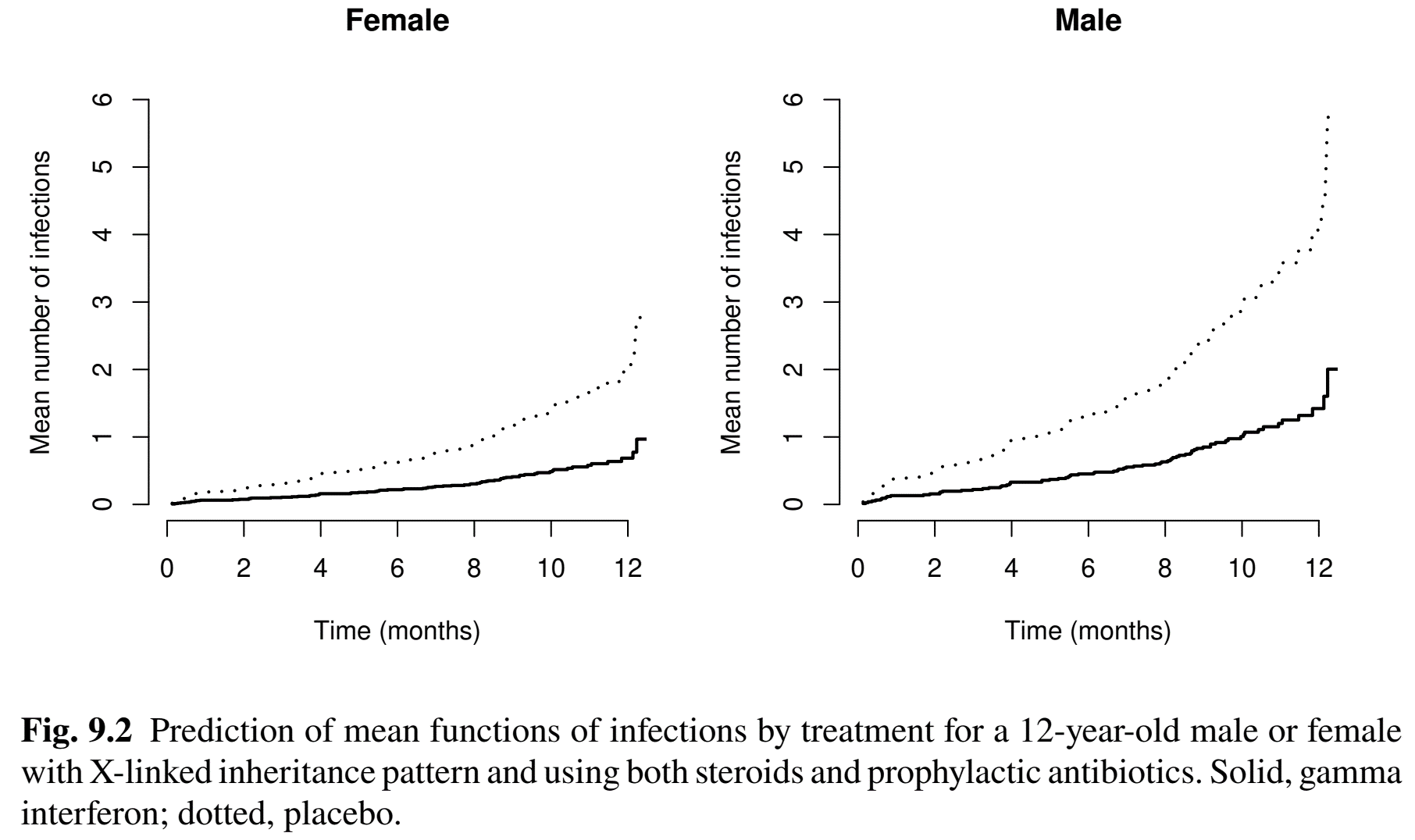
Prediction of Mean Frequency

  • LWYY (recommended)

Multivariate Approaches

Modeling Choices

  • Multivariate times
    • Total times: time from beginning to event \[T_1 < T_2 < T_3 < \cdots \]
    • Gap times: time from last to current event \[ U_1 = T_1,\,\, U_2 = T_2 - T_1,\,\, U_3 = T_3 - T_2,\,\, \ldots \]
  • Three classes of models
    • Marginal total times (Wei, Lin, and Weissfeld, 1989; WLW)
    • Conditional total times (Prentice, Williams, and Peterson, 1981; PWP-TT)
    • Gap times (Prentice, Williams, and Peterson, 1981; PWP-GT)

Marginal Total Times (WLW)

  • Model specification \[\begin{equation}\label{eq:rec:wlw} \pr(t\leq T_k<t+\dd t\mid T_k\geq t, Z)=\exp(\beta^\T Z)\dd\Lambda_{k0}(t) \end{equation}\]
    • Marginal Cox model for multivariate failure times \(T_1, \ldots, T_K\) (choose some cutoff \(K\))
    • Component-specific baseline function (why?)
    • \(\beta\): population-averaged log-hazard ratio for all recurrent events
    • Robust variance to account for correlation

Conditional Total Times (PWP-TT)

  • Model specification \[\begin{equation}\label{eq:rec:pwp_tt} \pr(t\leq T_k<t+\dd t\mid T_{k-1}<t\leq T_k, Z)=\exp(\beta^\T Z)\dd\Lambda_{k0}(t) \end{equation}\]
    • Rationale: subject at risk for \(k\)th event only after experiencing the \((k-1)\)th
    • \(\beta\): log-hazard ratio among those at risk for next event
    • Robust variance to account for correlation

Conditional Gap Times (PWP-GT)

  • Model specification \[\begin{equation}\label{eq:rec:pwp_gt} \pr(t\leq U_k<t+\dd t\mid U_k\geq t, Z)=\exp(\beta^\T Z)\dd\Lambda_{k0}(t). \end{equation}\]
    • A gap-time model: reset clock upon experiencing an event
    • Marginal Cox model for multivariate failure times \(U_1, \ldots, U_K\)
    • \(\beta\): log-hazard ratio for gaps between events
    • Robust variance to account for correlation

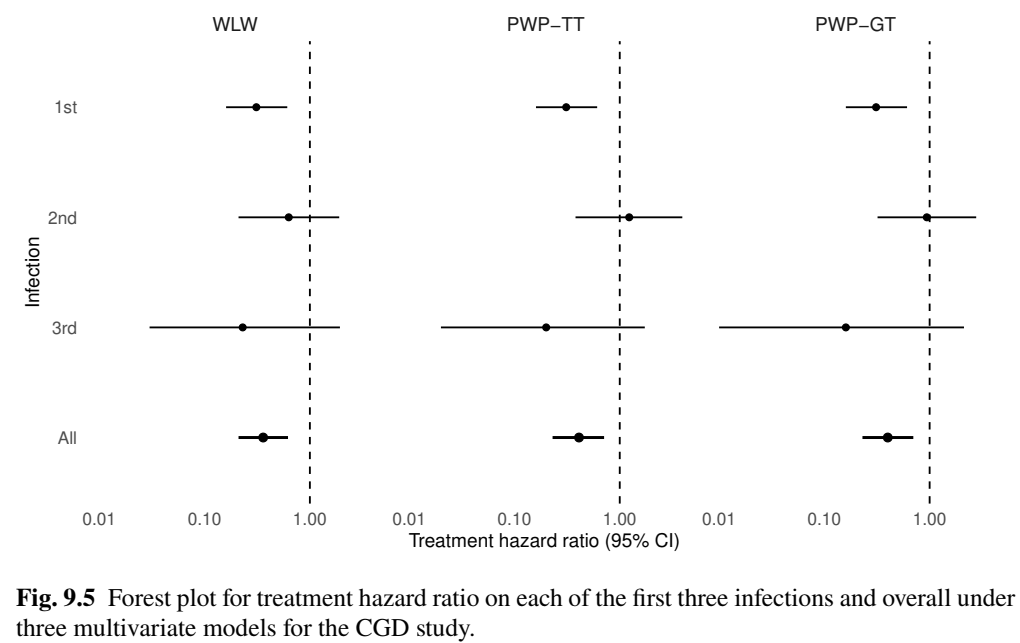
Conclusion

Notes (I)

  • LWYY (Lin, Wei, Yang & Ying, 2000)
    • Early explorations: Pepe and Cai (1993), Lawless and Nadeau (1995), Lawless et al. (1997)
  • PWP (Prentice, Williams, and Peterson, 1981)
    • Original version conditioned on event history
    • Robust versions are presented here

Notes (II)

  • Cook and Lawless (2007)

Summary (I)

  • Proportional intensity (Andersen-Gill)
    • Handles correlation by (internal) time-varying covariates
    • coxph(Surv(start, stop, status) ~ covariates)
  • Shared-frailty
    • Handles correlation by subject-level frailty
    • coxph(Surv(start, stop, status) ~ covariates + frailty(id, distribution = "gamma"))
  • Proportional rates (LWYY) - recommended
    • Handles correlation empirically via robust variance
    • coxph(Surv(start, stop, status) ~ covariates + cluster(id)

Summary (II)

  • Multivariate approaches
    • Marginal total times (WLW)
    • Conditional total times (PWP-TT)
    • Gap times (PWP-GT)
    • Software: reorganize/transform data and tweak coxph() for multiple failure times