Applied Survival Analysis

Chapter 8 - Multivariate Failure Times

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Introduction to frailty models

  2. Multivariate Cox model with shared frailty

  3. Example: A multi-center lung cancer study

  4. Marginal models and robust inference

  5. Example: the diabetic retinopathy study

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Frailty/Copula Models

Multivariate Failure Times

  • Two types of scenario
    • Multiple events on same subject
      • Cardiovascular endpoints: heart failure, myocardio-infarction (MI; heart attack), stroke, etc.
    • Clustering within group
      • Group: region, study center, family, pair of twins
  • Common challenge
    • Correlation of component failure times within the unit (subject, group, etc.)
  • Modelling strategies
    • Conditional (shared-frailty) models
    • Marginal (component-wise) models

Frailty Models: Concept

  • Target of inference: \(T=(T_1,\ldots, T_K)\)
    • Multivariate event times on same unit (subject or group)
    • Different or same failure types
  • Unit-specific frailty \(\xi\)
    • Latent (unobserved) factor shared by components within unit \(\to\) dependence
    • \(T_k\) \((k=1,\ldots, K)\): mutually independent given \(\xi\) with hazard \(\xi\eta'_k(t)\) \[\begin{equation}\label{eq:multi:fr_surv} \pr(T_1>t_1,\ldots,T_K>t_K\mid \xi)=\exp\left\{-\xi \sum_{k=1}^K \eta_k(t_k)\right\} \end{equation}\]
      • \(\xi\): nonnegative random variable with \(E(\xi)=1\)
      • \(\var(\xi)\uparrow\) \(\to\) greater between-unit variations \(\to\) stronger within-unit correlations
      • \(\eta_k(t)\): (frailty-)conditional cumulative hazard

Frailty Models: Joint Distribution

  • Marginal distribution
    • Assume \(\xi\sim g(\cdot \gamma)\) \[\begin{align}\label{eq:multi:joint_surv} S(t_1,\ldots, t_K)=&\pr(T_1>t_1,\ldots,T_K>t_K)\notag\\ =&\int_0^\infty\pr(T_1>t_1,\ldots,T_K>t_K\mid \xi)g(\xi;\gamma)\dd\xi\notag\\ =&\int_0^\infty\exp\left\{-\xi \sum_{k=1}^K \eta_k(t_k)\right\}g(\xi;\gamma)\dd\xi, \end{align}\]

Marginal component-wise distribution

  • Survival function: \(S_k(t)=\int_0^\infty\pr(T_k>t\mid\xi)g(\xi;\gamma)\dd\xi=\int_0^\infty\exp\left\{-\xi \eta_k(t)\right\}g(\xi;\gamma)\dd\xi\)
  • Cumulative hazard: \(\Lambda_k(t) = -\log S_k(t)=-\log\int_0^\infty\exp\left\{-\xi \eta_k(t)\right\}g(\xi;\gamma)\dd\xi\neq \eta_k(t)\)

Examples: Gamma Frailty (I)

  • Parametric families for \(\xi\)
    • Gamma
    • Positive stable
    • Inverse Gaussian
    • Log-normal
  • Gamma frailty model
    • \(\xi\sim\mbox{Gamma}(\gamma, \gamma)\) \((\gamma >0)\) \[ g(u;\gamma)=\Gamma(\gamma)^{-1}\gamma^\gamma u^{\gamma-1}\exp\left(-\gamma u\right),\hspace{3mm}u>0 \]
      • \(\Gamma(\gamma)=\int_0^\infty x^{\gamma-1}\exp(-x)\dd x\)
      • \(E(\xi) = 1\), \(\var(\xi)=\gamma^{-1}\) (Exercise)

Examples: Gamma Frailty (II)

  • Implied joint marginal \[ S(t_1,\ldots, t_K)=\left\{1+\gamma^{-1}\sum_{k=1}^K \eta_k(t_k)\right\}^{-\gamma} \]
    • Correlated for \(0<\gamma<\infty\)
    • As \(\gamma\to\infty\), i.e., \(\var(\xi)\downarrow 0\), \(S(t_1,\ldots, t_K)\to\exp\{-\sum_{k=1}^K \eta_k(t_k)\}\)
  • Component-wise marginals \[S_k(t)=\left\{1+\gamma^{-1} \eta_k(t)\right\}^{-\gamma} \]
    • Marginal cumulative hazard: \(\Lambda_k(t)=\gamma\log\left\{1+\gamma^{-1} \eta_k(t)\right\}\neq\eta_k(t)\)

Examples: Positive Stable Frailty

  • One-sided version of Stable distribution
    • No explicit form for \(g(\cdot;\gamma)\) \((0<\gamma\leq 1)\)
    • Laplace transform \[\begin{equation}\label{eq:multi:stable_laplace} \int_0^\infty\exp(-x\xi)g(\xi;\gamma)\dd\xi=\exp(-x^\gamma) \end{equation}\]
    • Implies joint marginal \[\begin{equation}\label{eq:multi:stable_joint_survival} S(t_1,\ldots, t_K)=\int_0^\infty\exp\left\{-\xi \sum_{k=1}^K \eta_k(t_k)\right\}g(\xi;\gamma)\dd\xi=\exp\left[-\left\{\sum_{k=1}^K \eta_k(t_k)\right\}^\gamma\right] \end{equation}\]
      • \(\gamma\uparrow 1\) \(\to\) independence
    • Marginal cumulative hazard: \(\Lambda_k(t)=\eta_k(t_k)^\gamma\neq\eta_k(t)\)
      • Does preserve PH structure in regression

Copula Models

  • Copula: Joint distribution in terms of component marginals

  • Clayton copula

    • Induced by Gamma frailty \[ S(t_1,\ldots, t_K) = \left\{\sum_{k=1}^KS_k(t_k)^{-1/\gamma}-K+1\right\}^{-\gamma} \]

  • Gumbel-Hougaard copula

    • Induced by positive-stable frailty \[ S(t_1,\ldots, t_K) = \exp\left(-\left[\sum_{k=1}^K\{-\log S_k(t_k)\}^{1/\gamma}\right]^\gamma\right) \]

One Sample: Data

  • Observed data \[ (X_{ki}, \delta_{ki}),\hspace{5mm} k=1,\ldots, K;\,\,\, i=1,\ldots, n \]
    • \(X_{ki}=\min(T_{ki}, C_{ki})\)
    • \(T_{ki}\): \(T_k\) in \(i\)th unit
    • \(C_{ki}\): independent censoring time for \(T_{ki}\) (may be same across \(k\))
    • \(\delta_{ki} = I(T_{ki}\leq C_{ki})\)
    • \(N_{ki}(t) = I(X_{ki}\leq t, \delta_{ki} = 1)\)
  • Parameters: \(\theta=(\eta_1,\ldots, \eta_K, \gamma)\)
    • \(\eta_1,\ldots, \eta_K\): component-wise conditional cumulative hazards
    • \(\gamma\): frailty distribution parameter

One Sample: Estimation

  • Expectation-Maximization (EM) algorithm
    • With \(\xi\) as “missing” data
    • \(E\)-step (numerical integration) \[\begin{equation}\label{eq:multi:estep} \hat\xi_i^{(j+1)}=E\{\xi_i\mid (X_{ki}, \delta_{ki}): k=1,\ldots, K; \theta^{(j)}\} \end{equation}\]
    • \(M\)-step (weighted Nelsen-Aalen estimator; standard MLE) \[\begin{equation}\label{eq:multi:mstep_H} \eta_k^{(j+1)}(t)=\int_0^t\frac{\sum_{i=1}^n\dd N_{ki}(u)}{\sum_{i=1}^n\hat\xi_i^{(j+1)}I(X_{ki}\geq u)} \hspace{5mm}(k=1,\ldots, K) \end{equation}\] \[ \gamma^{(j+1)}=\arg\max_{\gamma}\sum_{i=1}^n\log g(\hat\xi_i^{(j+1)};\gamma) \]

Frailty Cox Models

Model Specification

  • Frailty-conditioned Cox models

    • \(T_1,\ldots, T_K\) mutually independent given \(Z\) and \(\xi\)

    • Conditional component-wise model \[\begin{align}\label{eq:multi:ph_cond} \lambda_k(t\mid Z, \xi)&= \xi\exp(\beta_k^\T Z) \eta_{k0}'(t)\\ \pr(T_k>t\mid Z,\xi)&=\exp\left\{-\xi\exp(\beta_k^\T Z) \eta_{k0}(t)\right\} \end{align}\]

    • Conditional joint survival \[\begin{equation}\label{eq:multi:fr_surv_reg} \pr(T_1>t_1,\ldots,T_K>t_K\mid Z,\xi)=\exp\left\{-\xi\sum_{k=1}^K\exp(\beta_k^\T Z) \eta_{k0}(t_k)\right\} \end{equation}\]

Implied Marginals

  • Gamma frailty
    • Non-proportional hazards \[ \Lambda_k(t\mid Z)=\gamma\log\left\{1+\gamma^{-1} \exp(\beta_k^\T Z)\eta_{k0}(t)\right\} \]
  • Positive-stable frailty
    • Proportional hazards \[ \Lambda_k(t\mid Z)=\exp(\gamma\beta_k^\T Z)\eta_{k0}(t)^\gamma \]
    • Special case where PH structure is preserved

Parametrizations

  • Same failure clustered in group \[\begin{align} \beta_1&=\cdots=\beta_K=:\beta\\ \eta_{10}(\cdot)&=\cdots=\eta_{K0}(\cdot)=:\eta_0(\cdot) \end{align}\]

  • Different failure types \[\begin{align} &\mbox{Different }\beta_k\\ &\mbox{Different }\eta_{k0}(\cdot) \end{align}\]

    • Same covariate effect: \(\beta_1=\cdots=\beta_K=:\beta\)
    • e.g., beta blocker has same reduction in risk of all MACEs

Estimation and Inference

  • Estimation
    • EM algorithm treating the \(\xi\) as missing data
    • \(E\)-step: \(\hat\xi_i^{(j+1)}=E\{\xi_i\mid (X_{ki}, \delta_{ki}, Z_i): k=1,\ldots, K; \theta^{(j)}\}\)
    • \(M\)-step: \(\hat\xi_i^{(j+1)}\)-weighted partial likelihood for \(\beta_k^{(j+1)}\) + Breslow estimator for \(\eta_{k0}^{(j+1)}(t)\)
  • Testing covariate effect on multiple components
    • \(Z_{\cdot 1}\): main treatment of interest \[ H_0: \beta_{11}=\beta_{21}=\cdots=\beta_{K1}=0 \]
    • \(\chi_K^2\): chi-square test with \(𝐾\) degrees of freedom

Software: survival::coxph() (I)

  • Scenario 1: Gamma-frailty with same \(\beta\) and \(\eta_0\)
    • Same failure grouped in cluster id
coxph(Surv(time, status) ~ covariates + 
        frailty(id, distribution = "gamma"))
  • Scenario 2: Gamma-frailty with same \(\beta\) and different \(\eta_{k0}\)
    • Different failure types enum in unit id with same covariate effect
    • Stratified Cox model by component (single \(\beta\); component- specific \(\eta_{k0}\))
coxph(Surv(time, status) ~ covariates + strata(enum)
      + frailty(id, distribution = "gamma"))

Software: survival::coxph() (II)

  • Scenario 3: Gamma-frailty with different \(\beta_k\) and \(\eta_{k0}\)
    • Different failure types enum in unit id with different covariate effects
    • Component specific \(\beta_k\) and \(\eta_{k0}\)
coxph(Surv(time, status) ~ covariates * strata(enum) + 
      frailty(id, distribution = "gamma"))

Multi-Institution Lung Cancer Study

Study Background

  • Study information
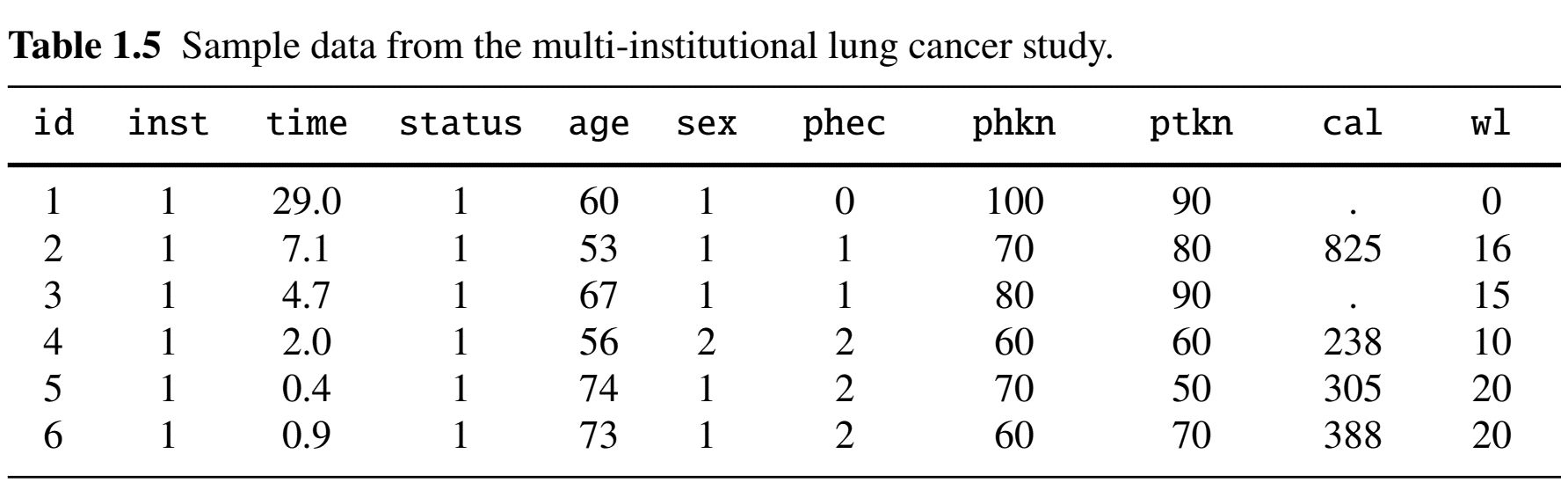
    • Population: 228 lung cancer patients grouped in 18 institutions
    • Endpoint: Death (link to follow-up plot)
    • Risk factors
      • Age (years); sex (1: male; 2: female); weight loss (pounds) in last six months
      • Physician-rated ECOG (0–3) and Karnofsky scores (50–100); Patient-rated Karnofsky score (50–100)

Cox Regression: Inference

  • Gamma frailty for correlation within institution

    • sex and physician-rated ECOG strongly predictive of mortality
    # Fit a Cox model with institution-specific frailty
# to account for correlation within institution
obj <- coxph(Surv(time, status) ~ age + factor(sex) + phec + phkn + 
            ptkn + wl + frailty(inst, distribution ="gamma"), data = data)

summary(obj)
#              exp(coef) exp(-coef) lower .95 upper .95
# age             1.0133     0.9869    0.9938    1.0331
# factor(sex)2    0.5333     1.8751    0.3751    0.7582
# phec            1.9984     0.5004    1.3460    2.9669
# phkn            1.0204     0.9800    1.0002    1.0410
# ptkn            0.9855     1.0147    0.9715    0.9998
# wl              0.9870     1.0132    0.9735    1.0006

Cox Regression: Prediction

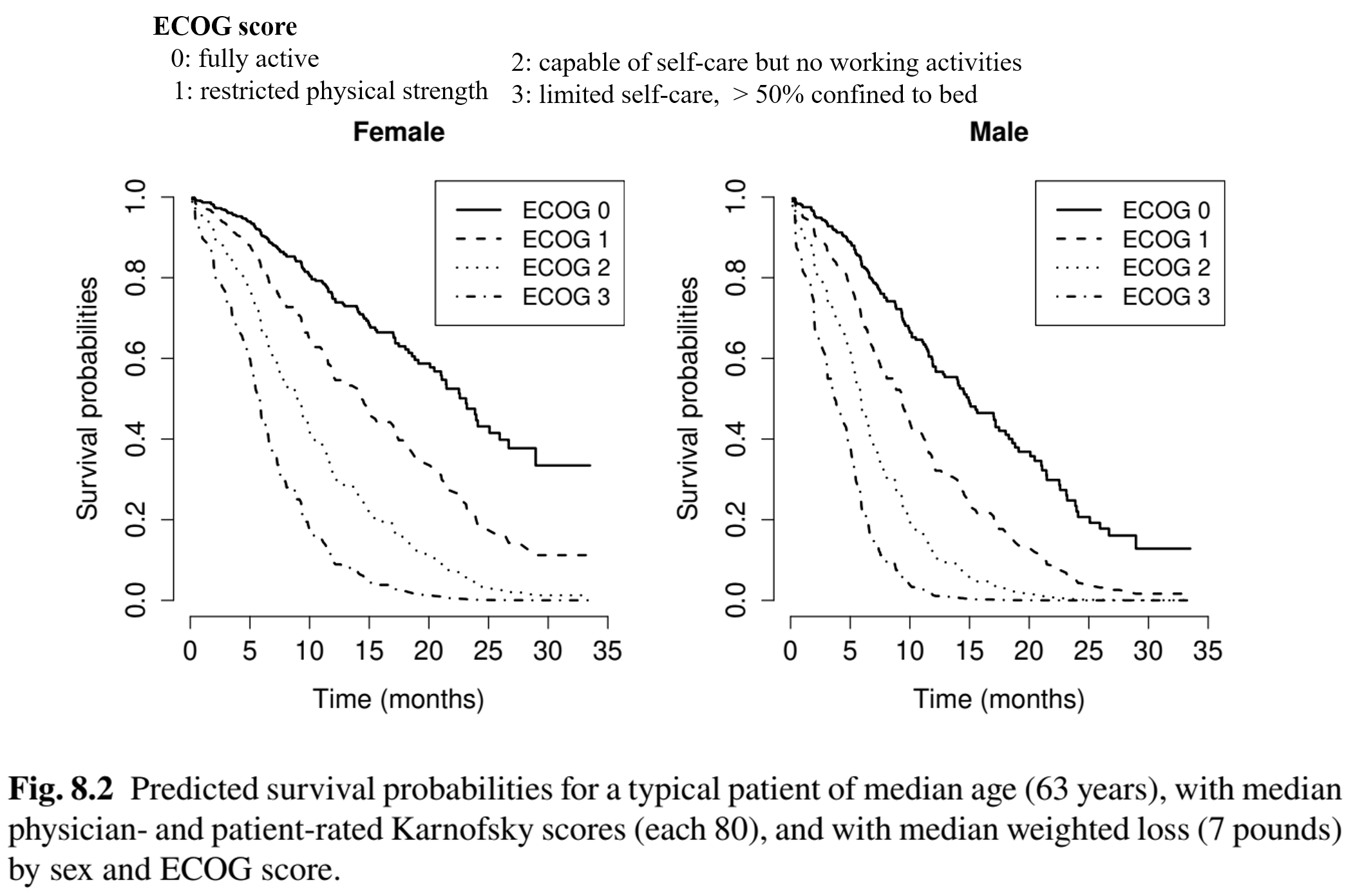
Marginal Models

Marginal Cox Models

  • Marginal models
    • Focusing on component-wise marginal distributions
      • Marginal distribution: distribution of a component across all units in population
    • No specification of joint distribution between components
    • Account for correlation empirically
  • Marginal Cox model \[\begin{equation}\label{eq:multi:marg_cox} \Lambda_k(t\mid Z)=\exp(\beta_k^\T Z)\Lambda_{k0}(t) \end{equation}\]
    • \(\beta_k\): population-averaged log-hazard ratios
      • Not comparable to unit-level \(\beta_k\) in frailty model
    • For same-type failure, constrain \(\beta_1=\cdots=\beta_K\) and \(\Lambda_{10}=\cdots=\Lambda_{K0}\)

Estimation (I)

  • Free \(\beta_k\) & \(\Lambda_{k0}\)
    • Solve \(U_{nk}(\hat\beta_k)=0\) \[\begin{align}\label{eq:multi:eek} U_{nk}(\beta_k)&=\Pn\int_0^\infty\left\{Z_i- \frac{\sum_{j=1}^nI(X_{kj}\geq t)Z_j\exp(\beta_k^\T Z_j)}{\sum_{j=1}^nI(X_{kj}\geq t)\exp(\beta_k^\T Z_j)}\right\}\dd N_{ki}(t) \end{align}\]
    • \(\hat\Lambda_{k0}(t)=\int_0^t\frac{\sum_{i=1}^n\dd N_{ki}(u)}{\sum_{i=1}^n I(X_{ki}\geq u)\exp(\hat\beta_k^\T Z_i)}\)
  • Same \(\beta\) & free \(\Lambda_{k0}\)
    • Solve \(U_{n}(\hat\beta)=0\) \[\begin{align}\label{eq:multi:ee_stra} U_{n}(\beta)&=\Pn\sum_{k=1}^K\int_0^\infty\left\{Z_i- \frac{\sum_{j=1}^nI(X_{kj}\geq t)Z_j\exp(\beta^\T Z_j)}{\sum_{j=1}^nI(X_{kj}\geq t)\exp(\beta^\T Z_j)}\right\}\dd N_{ki}(t) \end{align}\]

Estimation (II)

  • Same \(\beta\) & \(\Lambda_{0}\)
    • Solve \(U_{n}(\hat\beta)=0\) \[\begin{align}\label{eq:multi:ee_unstra} U_{n}(\beta)&=\Pn\sum_{k=1}^K\int_0^\infty\left\{Z_i- \frac{\sum_{k'=1}^K\sum_{j=1}^nI(X_{k'j}\geq t)Z_j\exp(\beta^\T Z_j)}{\sum_{k'=1}^K\sum_{j=1}^nI(X_{k'j}\geq t)\exp(\beta^\T Z_j)}\right\}\times\dd N_{ki}(t) \end{align}\]

Exercise: Breslow estimator

Construct proper Breslow estimators for the baseline function(s) given \(\hat\beta\) under:

  • Same \(\beta\) & free \(\Lambda_{k0}\)
  • Same \(\beta\) & \(\Lambda_{0}\)

Robust Variance: Sandwitch Estimator

  • Martingale not working
    • Conditional event rate given past \(\neq\) modeling target
    • Between-component dependence not specified
  • Robust variance
    • Works regardless of underlying dependence structure
    • Sandwich estimator \[ \hat\var(\hat\beta)=n^{-1}\hat A_n^{-1}\hat{\mathcal I}_n \hat A_n^{\T-1} \]
      • \(\hat A_n=\partial U_n(\hat\beta)/\partial\beta\)
      • \(\hat{\mathcal I}_n=\hat\var\{\sqrt n U_n(\beta)\}\): sample variance based on sum of independent units

Conditional vs Marginal Models

  • Comparison

Software: survival::coxph() (I)

  • Scenario 1: Marginal model with same \(\beta\) and \(\Lambda_0\)
    • Same failure grouped in cluster id
coxph(Surv(time, status) ~ covariates + cluster(id))
  • Scenario 2: Marginal model with same \(\beta\) and different \(\Lambda_{k0}\)
    • Different failure types enum in unit id with same covariate effect
      • Stratified Cox model by component (single \(\beta\); component- specific \(\Lambda_{k0}\))
coxph(Surv(time, status) ~ covariates + strata(enum)
      + cluster(id))

Software: survival::coxph() (II)

  • Scenario 3: Marginal model with different \(\beta_k\) and \(\Lambda_{k0}\)
    • Different failure types enum in unit id with different covariate effects
    • Component specific \(\beta_k\) and \(\Lambda_{k0}\)
coxph(Surv(time, status) ~ covariates * strata(enum) + 
      cluster(id))

Diabetic Retinopathy Study

Study Background

  • Study information
    • Design: randomized controlled trial of 197 diabetic patients, each with one eye receiving photocoagulation, the other eye left untreated as control (link to follow-up plot)
    • Questions: Whether treatment delays onset of blindness, and whether treatment effect depends on type of diabetes (adult or juvenile)

Marginal Cox Regression: Inference (I)

  • Marginal Cox model to handle correlation between eyes

    • Treatment effect differs by disease type substantially
    # Fit a bivariate marginal Cox model with treatment, diabetic type
# risk score, and treatment*type interaction as covariates
obj <- coxph(Surv(time, status) ~ trt + type + trt * type + risk
             + cluster(id), data = data)

summary(obj)
#                      coef exp(coef) se(coef) robust se      z Pr(>|z|)    
# trt              -1.29375   0.27424  0.27552   0.24614 -5.256 1.47e-07 ***
# typejuvenile     -0.37115   0.68994  0.19958   0.19535 -1.900  0.05745 .  
# risk              0.15342   1.16582  0.05636   0.05981  2.565  0.01031 *  
# trt:typejuvenile  0.88241   2.41672  0.35124   0.30962  2.850  0.00437 **

Marginal Cox Regression: Inference (II)

  • Efficiency gain by accounting for correlation
    • Robust: sandwich estimator
    • Naive: assuming two eyes are independent

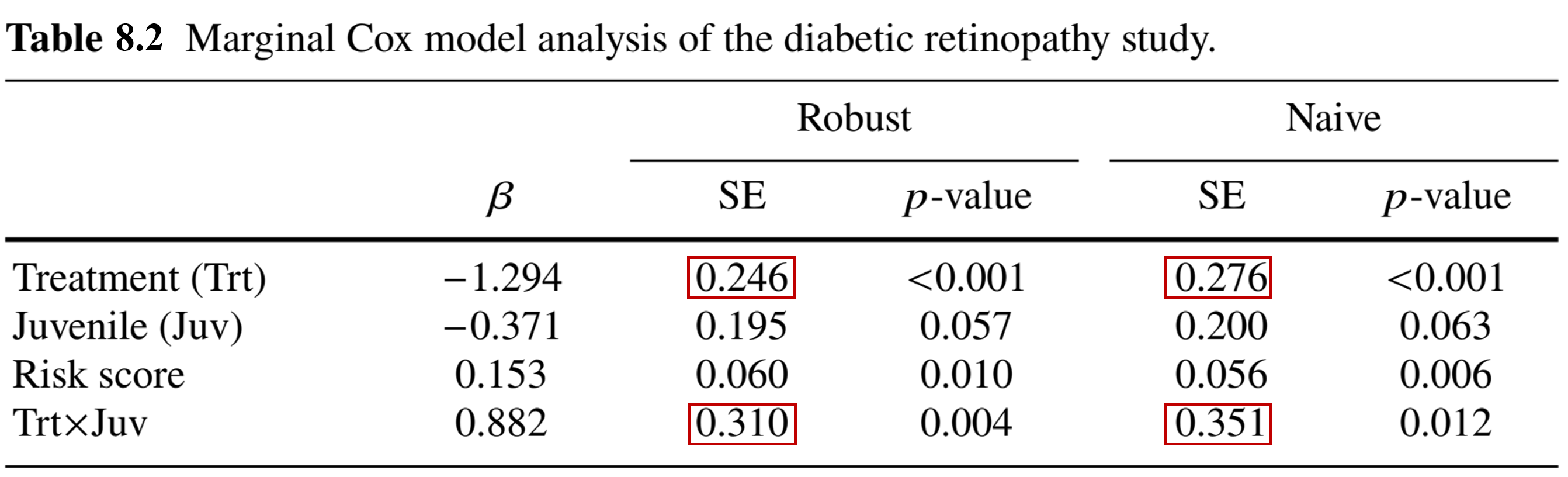
Marginal Cox Regression: Results

  • Treatment effect depends on disease type
    • Much greater reduction in risk of blindness of adult (type II?) than juvenile patients (type I?) (p-value = 0.004)
Diabetic type Hazard ratio
Adult \[ \exp(-1.294) = 27.4\% \]
Juvenile \[ \exp(-1.294 + 0.882)= 66.2\% \]

Marginal Cox Regression: Prediction

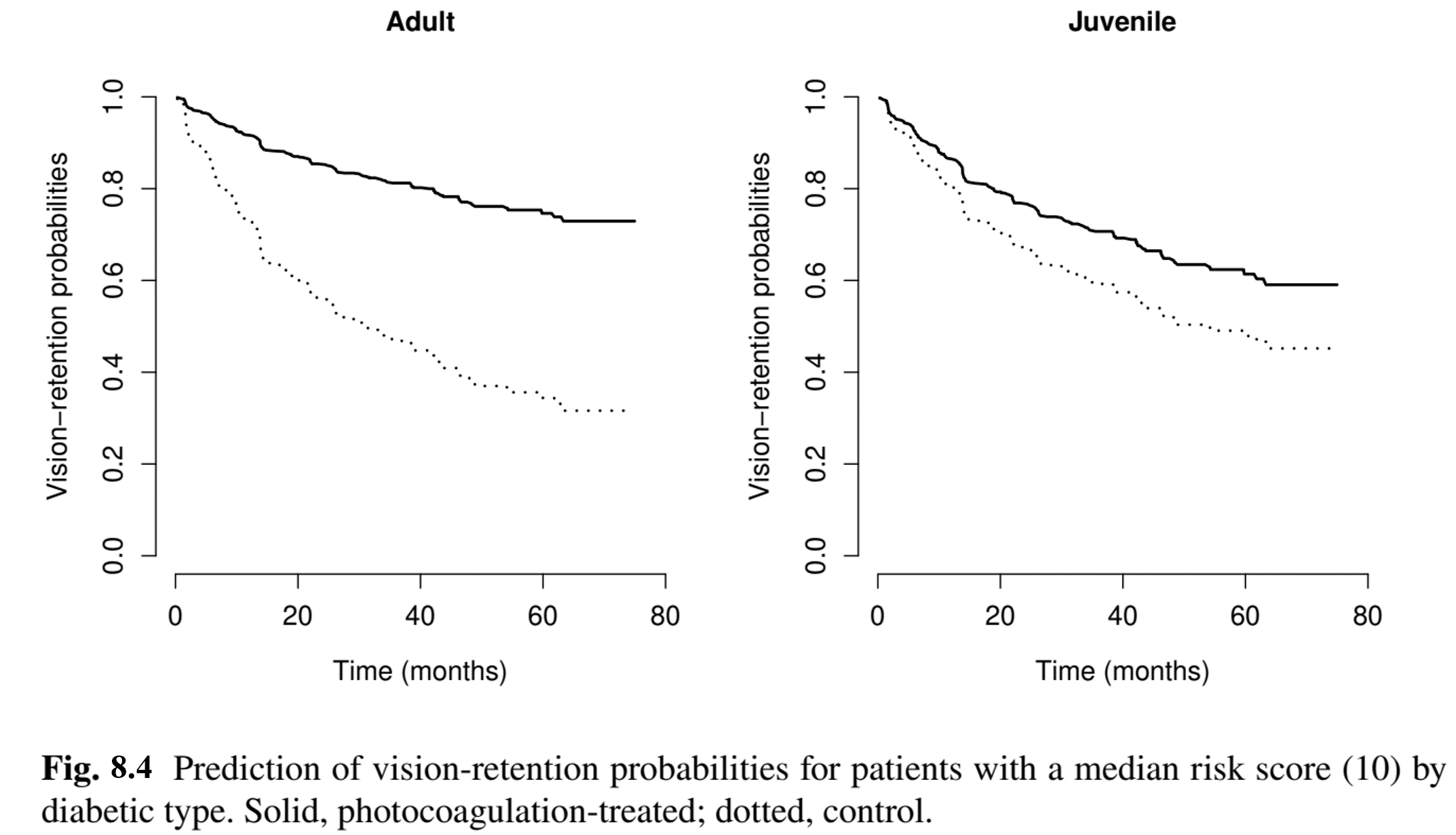
Conclusion

Notes (I)

Comparison with longitudinal analysis
Multivariate events Longitudinal data
Shared-frailty models Mixed-effects models
Marginal models Marginal models (GEE)
  • Frailty models = random intercepts \(\to\) random slopes \[ \pr(T_k>t\mid Z, b)=\exp\left\{-\exp(b^\T\tilde Z+\beta_k^\T Z)\eta_{k0}(t)\right\} \]
    • \(\tilde Z\) a subset of \(Z\)
    • \(b\sim_\mbox{e.g.} MVN(0, \Sigma)\)

Notes (II)

  • Hougaard (2000)

Summary

  • Shared-frailty Cox model \[ \pr(T_k>t\mid Z,\xi)=\exp\left\{-\xi\exp(\beta_k^\T Z) \eta_{k0}(t)\right\} \]
    • Unit-specific \(\xi\) induces correlation
    • coxph(Surv(time, status) ~ covariates + frailty(id, distribution = "gamma"))
  • Marginal Cox model \[ \Lambda_k(t\mid Z)=\exp(\beta_k^\T Z)\Lambda_{k0}(t) \]
    • Robust sandwich estimator to account for correlation empirically
    • coxph(Surv(time, status) ~ covariates + cluster(id))