Applied Survival Analysis

Chapter 6 - Sample Size Calculation and Study Design

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Sample size for Cox model and RMST

  2. Impact of study design and censoring

  3. An example using pilot study

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Sample Size Estimation

Motivation

  • Sample size calculation
    • Ensure power (80% or 90%) to detect meaningful difference
      • Power: probability of rejecting \(H_0\) under alternative
    • Too small sample \(\to\) low power \(\to\) fail to reject \(H_0\) even if \(H_A\) is true
  • Input information
    • Hypothesized effect size: minimal important difference (MID)
      • Hazard ratio, difference in RMST, etc.
    • Desired power (0.8 or 0.9)
    • Significance level \(\alpha\) (0.05)
    • Group allocation ratio (1:1)

General Setting

  • Standardized test statistic \[\begin{equation}\label{eq:design_form} S_n=\sqrt n T_n/\hat\sigma_n \stackrel{H_0}{\sim}\mathcal N(0, 1) \end{equation}\]
    • \(\sqrt n T_n\stackrel{H_0}{\sim}\mathcal N(0,\sigma_0^2)\); \(\,\) \(\hat\sigma^2_n=\) Estimator of \(\sigma_0^2\)
    • \(T_n\): Test statistic converging at \(n^{-1/2}\) rate as \(n\to\infty\)
  • Level-\(\alpha\) test
    • Reject \(H_0\) if \(|S_n|>z_{1-\alpha/2}\)
    • \(z_{1-\alpha/2}\): \(100(1-\alpha/2)\) percentile of standard normal
qnorm(0.975)
# [1] 1.959964

General Derivation

  • Effect size \(\theta\)
    • \(H_0: \theta = 0\); \(\,\) \(H_A: \theta\neq 0\)
      • \(\theta=\) log-hazard ratio under Cox model
      • \(\theta =\) difference in RMST
  • Suppose under \(H_A\)
    • Mean of test statistic (\(\theta=\) MID) \[ E_\theta(T_n)\approx f(\theta) \]
      • \(f(\theta)\) is some function with \(f(0)=0\) (centered under \(H_0\))
    • Then, \[S_n=\sqrt n T_n/\hat\sigma_n \stackrel{H_A}{\sim} \mathcal N\{\sqrt nf(\theta)/\sigma_0, 1\}\]
      • \(f(\theta)/\sigma_0\): signal-to-noise ratio

General Formula

  • Power requirement \[ \pr_\theta(|S_n|>z_{1-\alpha/2})\geq\gamma \]
    • \(\gamma\): desired power (0.8 or 0.9)
    • Use \(S_n \sim \mathcal N\{\sqrt nf(\theta)/\sigma_0, 1\}\) to solve for \(n\)
  • Sample size formula \[\begin{equation}\label{eq:design_ss_gen} n=\frac{\sigma_0^2(z_{1-\alpha/2}+z_\gamma)^2}{f(\theta)^2} \end{equation}\]
    • Find mean \(f(\theta)\) and variance \(\sigma_0^2\)

Case Study: Cox Model

  • Partial-likelihood score/log-rank test
    • Test statistic \(T_n = U_n(0)\)
      • Equivalent to log-rank test under \(Z = 1, 0\)
      • \(f(\theta)=E\{U_n(0)\}\approx\theta q(1-q)\psi\) and \(\sigma_0^2=q(1-q)\psi\)
      • \(q=N_1/n\): proportion randomized to treatment
      • \(\theta\): log-hazard ratio
      • \(\psi=\int_0^\infty \pi(t)\lambda_0(t)\dd t=\pr(T\leq C)\): proportion of failure observed, where \(\pi(t)=\pr(X> t)\)
  • Sample size formula \[\begin{equation}\label{eq:cox_sample_size} n= \frac{(z_{1-\alpha/2}+z_{\gamma})^2}{q(1-q)\psi\theta^2} \end{equation}\]
    • Expected number of events \(n\psi = (z_{1-\alpha/2}+z_{\gamma})^2/\{q(1-q)\theta^2\}\)

Case Study: RMST

  • Difference in \(\tau\)-RMST
    • Test statistic \(T_n = \hat\theta(\tau)=\hat\mu_1(\tau) - \hat\mu_0(\tau)\)
      • \(f(\theta)=E\{\hat\theta(\tau)\}\approx\theta(\tau)\) and \(\sigma_0^2=\var\{\sqrt n\hat\theta(\tau)\}\approx q^{-1}(1-q)^{-1}\zeta(\tau)\)
      • \(\zeta(\tau)=\int_0^\tau R_0(\tau;t)^2\pi(t)^{-1}\lambda_0(t)\dd t\)
      • \(R_0(\tau;t)=\int_t^\tau S_0(t)\dd t\)
      • \(S_0(t)\) and \(\lambda_0(t)\): survival/hazard functions in control
  • Sample size formula \[\begin{equation}\label{eq:rmst_sample_size} n= \frac{\zeta(\tau)(z_{1-\alpha/2}+z_{\gamma})^2}{q(1-q)\theta(\tau)^2} \end{equation}\]

Impact of Study Design

Dependence on Censoring

  • Two types of parameters
    • The failure factor: \(S_0(t), \lambda_0(t)\), log-HR, \(\theta(\tau)\)
      • Use domain knowledge (or pilot study data) to specify (or estimate)
    • The censoring factor \[ \pi(t)=\pr(X>t)=S_0(t)G(t) \]
      • \(G(t)=\pr(C > t)\)
      • Involved in \(\psi\) for log-rank (Cox) and \(\zeta(\tau)\) for RMST
  • Censoring depends on study design
    • Initial period of subject accrual
    • Additional follow-up

Simplified Model

  • Parametric set-up
    • \(T\sim\mbox{Expn}(\lambda_0)\)
    • Loss to follow-up (LTFU) \(\sim\mbox{Expn}(\lambda_L)\)
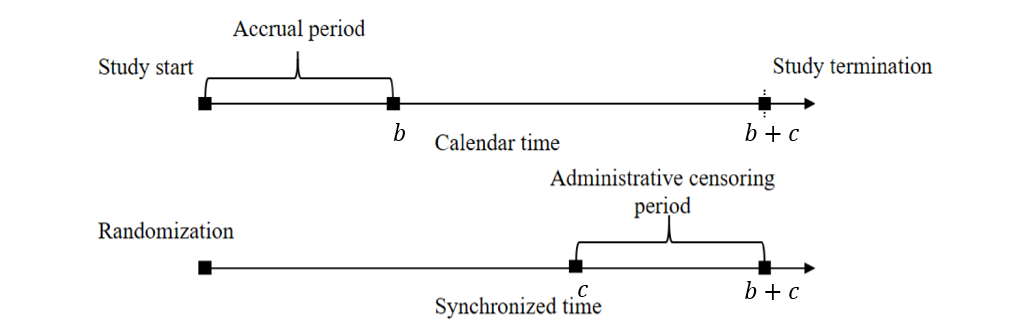
    • Administrative censoring \(\sim\mbox{Unif}[c, b + c]\)
      • Uniform accrual in \([0, b]\)
      • Subsequent follow-up time \(c\)

Model-Based Expressions

  • Under this set-up
    • Censoring survival function \[\begin{equation}\label{eq:design:censoring} G(t;\lambda_L, b, c):=\pr(C>t)=\left\{\begin{array}{ll} \exp(-\lambda_L t)& 0\leq t\leq c\\ b^{-1}(c+b-t)\exp(-\lambda_L t) & c<t<c+b \\ 0& t\geq c+b. \end{array}\right. \end{equation}\]
      • \(\psi\) for log-rank (closed-form) \[\begin{equation}\label{eq:cox:psi} \psi(\lambda_0,\lambda_L, b, c)=\frac{\lambda_0}{\lambda_0+\lambda_L}\left[1-\exp\{-(\lambda_0+\lambda_L)c\} \frac{1-\exp\{-(\lambda_0+\lambda_L)b\}}{(\lambda_0+\lambda_L)b}\right] \end{equation}\]
      • \(\zeta(\tau)\) for RMST (needs numerical integration) \[\begin{equation}\label{eq:design:rmst_zeta} \zeta(\tau; \lambda_0, \lambda_L, b, c)=\lambda_0^{-1}\int_0^\tau\{\exp(-\lambda_0 t)-\exp(-\lambda_0 \tau)\}^2\exp(\lambda_0 t)G(t;\lambda_L, b, c)^{-1}\dd t \end{equation}\]
    • Plug \(\psi\) or \(\zeta(\tau)\) back into sample size formulas

Programming the Functions (I)

  • \(G(t;\lambda_L, b, c)\): Survival function for censoring
Gfun <- function(t, lambdaL, b, c){
  Gt <- ifelse(t <= c, exp(- lambdaL * t),
    ifelse(t < c + b, exp(- lambdaL * t) * (b + c - t ) / b, 0))
  return(Gt)
}
  • \(\psi(\lambda_0,\lambda_L, b, c)\): \(\psi\) parameter for log-rank
psi_fun <- function(lambda0, lambdaL, b, c){
        lambda <- lambda0 + lambdaL
   psi <- lambda0 / lambda * 
     (1 - exp(- lambda * c) * (1 - exp(- lambda * b)) / (lambda * b))
   return(psi)
}

Programming the Functions (II)

  • \(\zeta(\tau; \lambda_0, \lambda_L, b, c)\): \(\zeta(\tau)\) for RMST
# ------ integrand function --------------------------------
zeta_integrand <- function(t, tau, lambda0,lambdaL, b, c){
  integrand <- (exp(- lambda0 * t) - exp( - lambda0 * tau))^2*
      exp(lambda0 * t)/(Gfun(t, lambdaL, b, c) * lambda0)
  return(integrand)
}

# ------ numerical integration by integrate() --------------
zeta_fun <- function(tau, lambda0, lambdaL, b, c){
  f <- function(t){
   return(zeta_integrand(t, tau, lambda0, lambdaL, b, c))
  }
  zeta <- integrate(f, lower = 0, upper = tau)
  return(zeta$value)
}

How to Specify Parameters

  • Specification of \((\lambda_0, \lambda_L, b, c)\)
    • \(\lambda_0\) (and \(\lambda_L\)): use domain knowledge or estimate from historical data
    • \(\hat\lambda_0\): (crude) event rate (see Chapters 1 & 2) \[ \hat\lambda_0 = \frac{\mbox{Number of events}}{\mbox{Total person-time}} \]
    • \(b, c\): determined by current study design
  • Specification of \(\theta\)
    • Supplied by investigator based on domain knowledge (MID)

An Example

Example: GBC as Pilot Study (I)

  • Design objective
    • A randomized controlled trial to evaluate hormonal treatment on relapse-free survival of post-menopausal breast cancer patients
    • \(b=2\) years of accrual; \(c=3.5\) years subsequent follow-up
  • GBC pilot data
    • \(\hat\lambda_0=0.174\) per person-year based on \(n=209\)
  • Other parameters
    • Set \(\lambda_L=0.01\) per person-year
    • \(\lambda_1\): (constant) hazard rate in treatment, taking a range of values
    • HR: \(\lambda_1/\lambda_0\); difference in RMST (Exercise)

Example: GBC as Pilot Study (II)

  • Sample sizes for Cox (log-rank), 3y-RMST, 5y-RMST

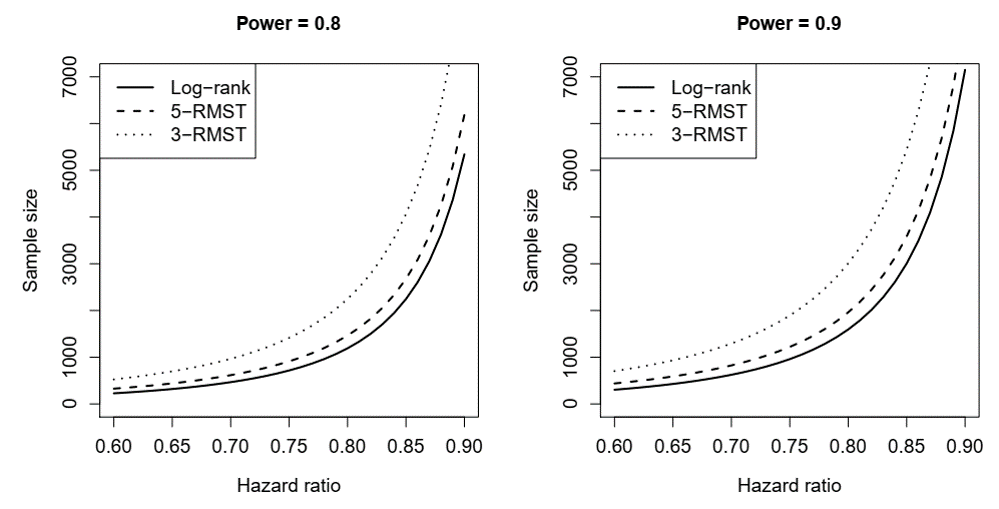
Conclusion

Notes (I)

  • SAS code for log-rank
PROC POWER;
   TWOSAMPLESURVIVAL TEST=LOGRANK
      HAZARDRATIO = 0.7, 0.75, 0.8, 0.85, 0.9
      REFSURVEXPHAZARD = 0.174 
      ACCRUALTIME = 2
      FOLLOWUPTIME = 3.5
      GROUPLOSSEXPHAZARDS = (0.01, 0.01)
      NTOTAL = .
      POWER = 0.8, 0.9;
RUN;
  • Sample size formula for log-rank (Schoenfeld, 1981)
    • Freedman (1982): more accurate when \(\theta\) is large
    • Schoenfeld (1983): covariate adjusted test (Schoenfeld, 1983)

Notes (II)

  • R-package npsurvSS (Yung and Liu, 2020)
    • Various tests (e.g., weighted log-rank, RMST, survival probability tests)
    • Non-exponential event/ LTFU, non-uniform accrual
# Set up the two groups
control <- create_arm(
              # Parameter set-up for control
                      )
treatment <- create_arm(
              # Parameter set-up for treatment
                      )
# Compute sample size
size_two_arm(control, treatment, 
      test = list(list(test="weighted logrank"), # Log-rank test
                  list(test="rmst difference", milestone=3), # 3y-RMST 
                  list(test="rmst difference", milestone=5)) # 5y-RMST 
              )

Summary

  • Sample size calculations
    • Cox (log-rank) \[\begin{equation} n= \frac{(z_{1-\alpha/2}+z_{\gamma})^2}{q(1-q)\psi\theta^2} \end{equation}\]
    • \(\tau\)-RMST \[\begin{equation} n= \frac{\zeta(\tau)(z_{1-\alpha/2}+z_{\gamma})^2}{q(1-q)\theta(\tau)^2} \end{equation}\]
    • \(\psi\) or \(\zeta(\tau)\) calculated under simplifying assumptions
      • Exponential failure and LTFU
      • Uniform accrual