Applied Survival Analysis

Chapter 5 - Other Non-/Semi-Parametric Methods

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Restricted Mean Survival Time (RMST)

  2. Additive Hazards (AH) Model

  3. Proportional Odds (PO) Model

  4. Accelerated Failure Time (AFT) Model

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Restricted Mean Survival Time (RMST)

Motivation

  • Limitations of hazard ratio
    • Proportionality
    • Depends on time frame in case of non-proportionality
  • Alternative metric
    • \(\tau\)-year survival rate \(S(\tau)\) for a fixed \(\tau\)
      • \(5\)-year survival rates for cancer patients
    • \(S_1(\tau) - S_0(\tau)\): increase in survival rate by treatment vs control
    • Limitation: cross-sectional survival status at \(\tau\)
      • Distribution of \(T\) in \([0, \tau]\) ignored
      • Delay of death within \([0, \tau]\) not captured

Definition and Interpretation

  • Restricted mean survival time (RMST) \[\mu(\tau)=E(T\wedge\tau)\]
    • a.k.a. Restricted mean life
    • Averaged time lived in the first \(\tau=5\) years
    • Restricted mean time lost (RMTL): \(L(\tau) = \tau - \mu(\tau)\)
    • Alternate expression (area under survival curve, AUC) \[\begin{equation}\label{eq:non_haz:auc} \mu(\tau)=\int_0^\tau S(t)\dd t. \end{equation}\]
      • Estimator \(\hat\mu(\tau)=\int_0^\tau \hat S(t)\dd t\), where \(\hat S(t)\) is KM estimator

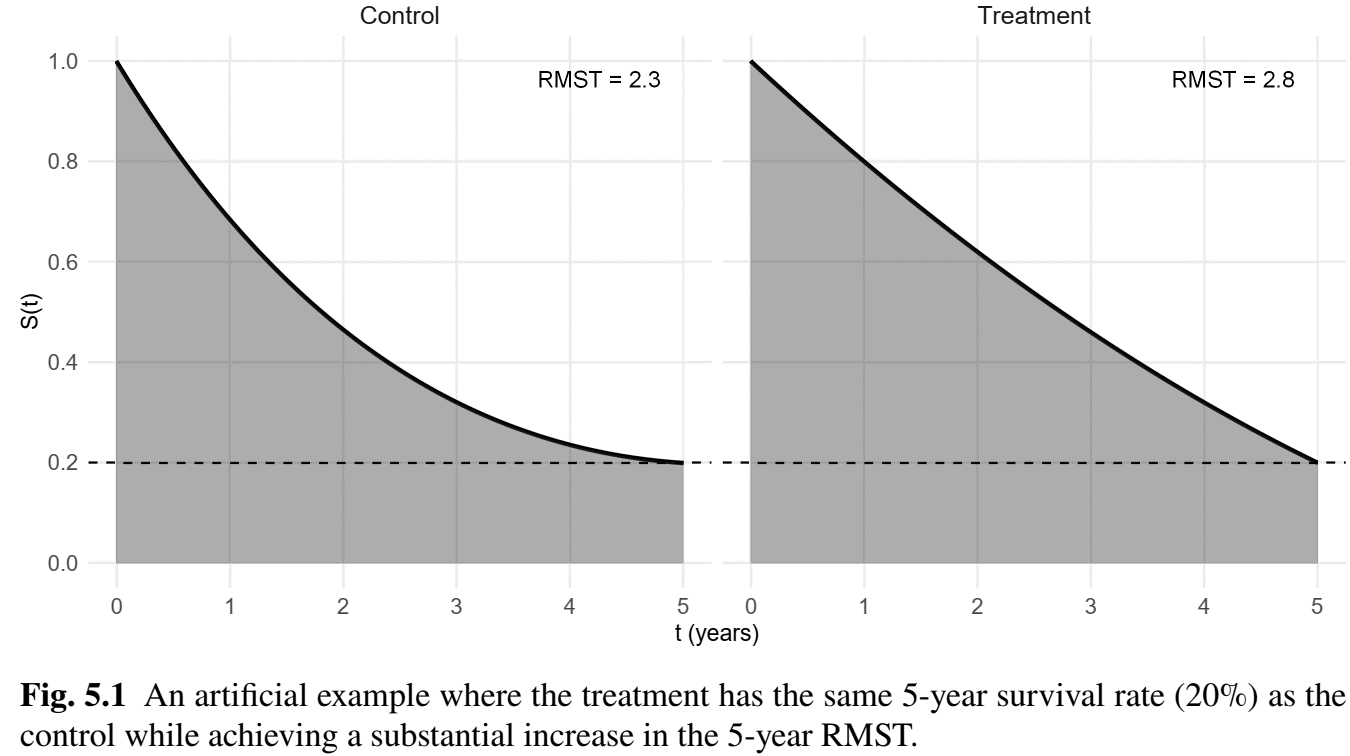
Survival Rate vs RMST

  • \(S(\tau)\) vs \(\mu(\tau)\)
    • \(S(\tau)\): survival status at \(\tau\)
    • \(\mu(\tau)\): summary of survival experience in \([0, \tau]\) (more information)

Two-Sample Inference

  • Effect size (\(a=1\): treatment; 0: control)
    • Additive: \(\mu_1(\tau)-\mu_0(\tau)\)
      • Average survival (event-free) time gained in \([0, \tau]\)
    • Multiplicative: \(\mu_1(\tau)/\mu_0(\tau)\) or \(L_1(\tau)/L_0(\tau)\)
      • Fold change in average survival time (lost) in \([0, \tau]\)
  • Estimation and inference
    • Plug in KM estimators \(\hat S_a(t)\) \((a= 1, 0)\)
    • Obtain \(\hat\var\{\hat\mu_a(\tau)\}\) by \[ \hat\mu_a(\tau) = \mbox{time-weighted sum of the }\hat S_a(t_j) \mbox{ up to }\tau \]
      • Greenwood’s formula for \(\hat\var\{\hat S_a(t_j)\}\)

Regression Models

  • Modeling target: conditional RMST \[ \mu(\tau\mid Z)=E(T\wedge \tau\mid Z) \]
  • Model specification \[ g\{\mu(\tau\mid Z)\}=\beta^\T Z \]
    • \(g(x) = x\): Additive model on RMST
      • Unit increases in \(Z\) increase \(\tau\)-RMST by \(\beta\)
    • \(g(x) = \log(x) \mbox{ or } \log(\tau -x)\): Multiplicative model on RMST/RMTL
      • Unit increases in \(Z\) change \(\tau\)-RMST/RMTL by \(\exp(\beta)\) times
    • \(Z = 1, 0\) \(\Rightarrow\) Two-sample additive/multiplicative effect sizes

Fitting Regression Models

  • Observed data

\[ (X_i, \delta_i, Z_i)\,\,\, i=1,\ldots, n \]

  • Inverse probability censoring weighting (IPCW) \[\begin{equation}\label{eq:nonhaz_rmst_ipcw} n^{-1}\sum_{i=1}^n \frac{\delta_i}{G(X_i\mid Z_i)}Z_i \{X_i\wedge\tau - g^{-1}(\hat\beta^\T Z_i)\} = 0, \end{equation}\]

    • \(G(t\mid Z) = \pr(C>t\mid Z)\): replace by model-based version
    • Works because \(E\left[\frac{\delta}{G(X\mid Z)}Z\{X\wedge\tau - g^{-1}(\beta^\T Z)\}\right]=0\) under \(C\indep T\mid Z\) (Exercise)

Software: survRM2::rmst2() (I)

  • Basic syntax for RMST analysis
library(survRM2)
# Two-sample or regression analysis of RMST
obj <- rmst2(time, status, arm, tau, covariates = NULL)
  • Input
    • (time, status): \((X, \delta)\)
    • arm: vector of indicators (1-0) for treatment vs control
    • tau: scaler \(\tau\)
    • covariates: optional covariate matrix (or data frame)

Software: survRM2::rmst2() (II)

  • Two-sample output (covariates = NULL)
    • obj$RMST.arm1 & obj$RMST.arm0: two lists of group-wise inference results for arm = 1 and 0
    • obj$unadjusted.result: matrix containing estimates, 95% confidence intervals, and \(p\)-values for \(\mu_1(\tau) - \mu_0(\tau)\), \(\mu_1(\tau)/\mu_0(\tau)\), and \(L_1(\tau)/L_0(\tau)\)
  • Regression output (covariates supplied)
    • obj$RMST.difference.adjusted: regression results for \(g(x) =x\)
    • obj$RMST.ratio.adjusted: regression results for \(g(x) = \log(x)\)
    • obj$RMTL.ratio.adjusted: regression results for \(g(x) = \log(\tau - x)\)

RMST: German Breast Cancer (I)

  • Endpoint: 5-year restricted mean relapse-free survival time
    • Two-sample: Hormone (arm=1) vs non-hormone (arm=0)
# Two sample: hormonal and non-hormonal groups on 5-year RMST
obj <- rmst2(time = df$time / 12, status = df$status, 
            arm = df$hormone - 1, tau = 5)
obj
# Restricted Mean Survival Time (RMST) by arm 
#              Est.    se lower .95 upper .95
# RMST (arm=1) 3.87 0.104     3.666     4.074
# RMST (arm=0) 3.46 0.084     3.295     3.625
# 
# Restricted Mean Time Lost (RMTL) by arm 
#              Est.    se lower .95 upper .95
# RMTL (arm=1) 1.13 0.104     0.926     1.334
# RMTL (arm=0) 1.54 0.084     1.375     1.705

RMST: German Breast Cancer (II)

  • Two-sample

    • Hormone increases 5-year RMST by 0.41 years (\(p\)=0.002)
    # Between-group contrast 
#                       Est. lower .95 upper .95     p
# RMST (arm=1)-(arm=0) 0.410     0.148     0.672 0.002
# RMST (arm=1)/(arm=0) 1.118     1.042     1.201 0.002
# RMTL (arm=1)/(arm=0) 0.734     0.595     0.905 0.004
#
#-----  Graphic -------------------------------------------------
# Graphical display of the group-specific RMST 
# as area under the KM curves
plot(obj, xlab="Time (years)", ylab = "Relapse-free survival",
     col.RMST = "gray", col.RMTL = "white", cex.lab = 1.2,
     cex.axis = 1.2, col = "black", xlim = c(0,5))

RMST: German Breast Cancer (III)

  • Two-sample

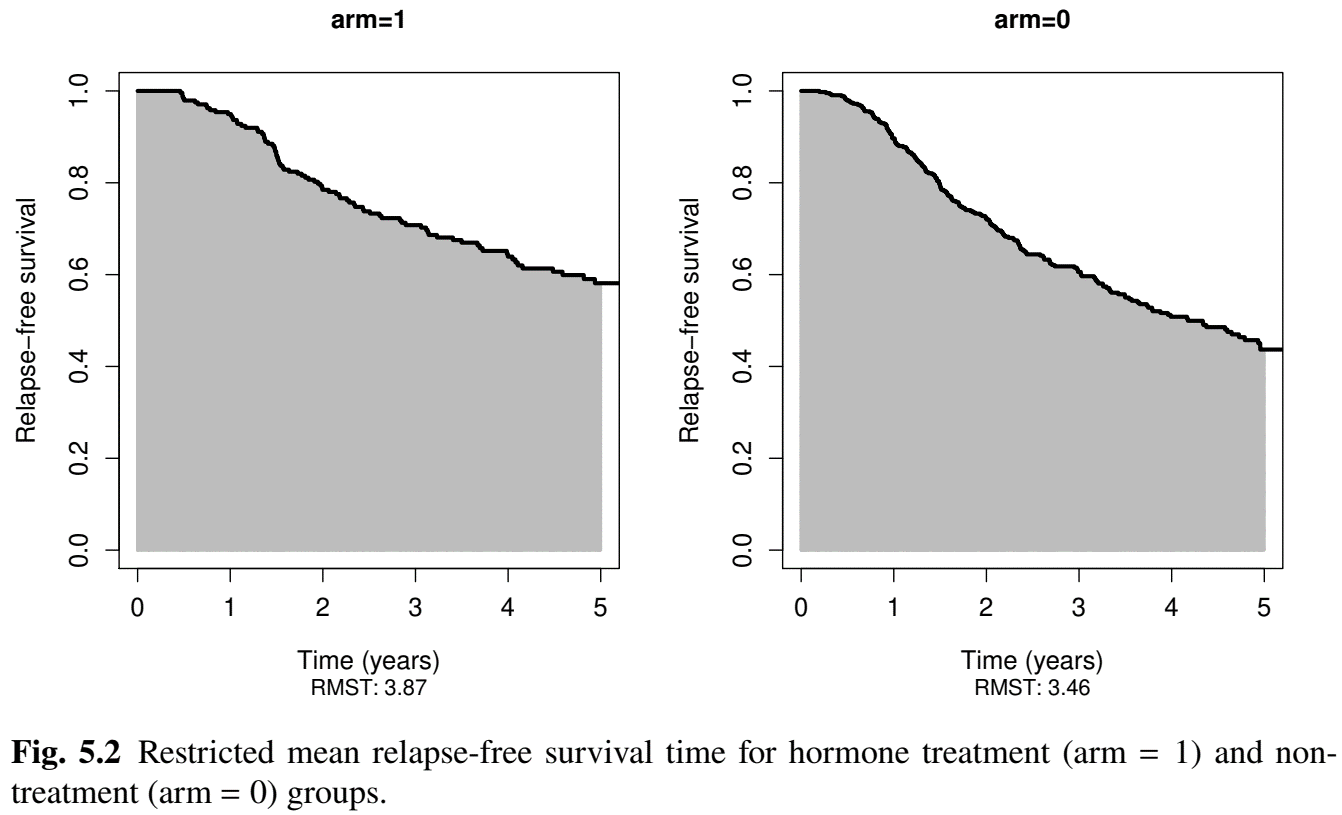
RMST: German Breast Cancer (IV)

  • Regression
    • Hormone extends 5-year RMST by 1.137 - 1 = 13.7% (\(p<\) 0.001)
# Regression with all the other covariate
obj_reg <- rmst2(time = df$time / 12, status = df$status, 
            arm = df$hormone - 1, covariates = df[, 5:11], tau = 5)
#----- Print out multiplicative model on RMST ---------------
obj_reg$RMST.ratio.adjusted
#             coef se(coef)      z     p exp(coef) lower .95 upper .95
# intercept  1.574    0.153 10.257 0.000     4.824     3.571     6.516
# arm        0.129    0.039  3.318 0.001     1.137     1.054     1.227
# age        0.006    0.004  1.537 0.124     1.006     0.998     1.013
# meno      -0.111    0.072 -1.539 0.124     0.895     0.777     1.031
# size      -0.004    0.002 -2.132 0.033     0.996     0.992     1.000
# grade     -0.120    0.035 -3.463 0.001     0.887     0.828     0.949
# nodes     -0.032    0.006 -5.421 0.000     0.969     0.957     0.980
# ...

Additive Hazards (AH) Model

Semiparametric AH Model

  • Additive, not multiplicative (Cox), hazards \[\begin{equation}\label{eq:non_haz:add_haz} \lambda(t\mid Z)=\lambda_0(t)+\beta^\T Z, \end{equation}\]
    • \(\beta_k\): risk difference (attributable risk) with one unit increase in \(Z_{\cdot k}\)
    • Unit: per (person-)time
  • “Score” equation
    • \(\hat\beta\): explicit solution to \(U_n(\hat\beta)=0\) (Lin and Ying, 1994) \[\begin{equation} U_n(\beta) = n^{-1}\sum_{i=1}^n\int_0^\tau\left\{Z_i -\frac{\sum_{j=1}^n I(X_j\geq t)Z_j}{\sum_{j=1}^n I(X_j\geq t)}\right\} \{\dd N_i(t) - I(X_i\geq t)\beta^\T Z_i \dd t\}, \end{equation}\]

AH Model Extensions

  • Time-varying covariates \[\begin{equation} \lambda(t\mid Z) =\lambda_0(t)+\beta^\T Z(t) \end{equation}\]

  • Residuals

    • Cox-Snell, score, martingale/deviance

  • Aalen’s nonparametric AH model \[\begin{equation}\label{eq:non_haz:add_haz1} \lambda(t\mid Z)=\lambda_0(t)+\beta(t)^\T Z(t), \end{equation}\]

    • Least-squares type estimates for \(B(t)=\int_0^t\beta(s)\dd s\)
    • Can be used to check constancy of \(\beta\)

Software: addhazard::ah()

  • Basic syntax for semiparametric AH
library(addhazard)
# Fit semiparametric AH model
obj <- ah(Surv(time, status) ~ covariates, ties = FALSE)
  • Input
    • Surv(time, status) ~ covariates: same formula as in coxph()
    • ties = FALSE: specify and de-tie time (add a small noise)
  • Output: an object of class ah
    • obj$coef: \(\hat\beta\), obj$var: \(\hat\var(\hat\beta)\)
    • summary(obj): outputs regression table

Software: timereg::aalen()

  • Basic syntax for Aalen’s nonparametric AH
library(timereg)
# Fit Aalen's nonparametric AH model
obj <- aalen(Surv(time, status) ~ covariates)
  • Input
    • Surv(time, status) ~ covariates: same formula as coxph()
  • Output: an object of class aalen
    • obj$cum: matrix containing \(t\) and \(\hat B(t)\)
    • obj$var: matrix containing \(t\) and pointwise \(\hat\var\{\hat B(t)\}\)
    • summary(obj): outputs test results for \(H_0: \beta(t)\equiv 0\)

AH: German Breast Cancer (I)

  • Semiparametric AH model
    • Hormone reduces relapse/death rate by 0.050 per person-year
# Add a small random number to time to get rid of ties
df$time.dties <- df$time/12 + runif(nrow(df),0, 1e-12) 
# fit an additive hazard model
obj <- ah(Surv(time.dties, status) ~ hormone + meno + age + size + 
            grade + nodes + prog + estrg, data = df, ties = FALSE)
# print out summary
summary(obj)
#               coef         se   lower.95   upper.95      z  p.value    
# hormone -0.0497713  0.0170343 -0.0831585 -0.0163842 -2.922  0.00348 ** 
# meno     0.0373581  0.0242005 -0.0100749  0.0847911  1.544  0.12266    
# age     -0.0011667  0.0013891 -0.0038895  0.0015560 -0.840  0.40096    
# size     0.0010200  0.0007299 -0.0004107  0.0024506  1.397  0.16231   
# ...

AH: German Breast Cancer (II)

  • Semi- vs. Non-parametric

Proportional Odds (PO) Model

Semiparametric PO Model

  • Model specification \[\begin{equation}\label{eq:non_haz:po} \log\left\{\frac{1-S(t\mid Z)}{S(t\mid Z)}\right\}=h_0(t)+\beta^\T Z, \end{equation}\]
    • \(h_0(t)\): nonparametric (non-decreasing) baseline cumulative log-odds
    • Fix \(t\) \(\to\) logistic regression for \(I(T\leq t)\)
      • Time-varying intercept, constant odds ratio
    • Proportional odds \[\begin{equation}\label{eq:non_haz:poprop} \frac{\{1-S(t\mid z_1)\}/S(t\mid z_1)}{\{1-S(t\mid z_2)\}/S(t\mid z_2)}=\exp\{\beta^\T(z_1-z_2)\}. \end{equation}\]
      • \(\exp(\beta_k)\): odds ratio for an early event (regardless of cut-off) with one unit increase in \(Z_{\cdot k}\)

Estimation and Extension

  • Estimation and inference
    • Nonparametric MLE: Joint maximization w.r.t. \(\beta\) and the \(\Delta h(t_j)= h(t_j) - h(t_j-)\) \((j=1,\ldots, m)\)
  • Semiparametric transformation models \[\begin{equation}\label{eq:non_haz:linear_trans} g\{F(t\mid Z)\}=h_0(t)+\beta^\T Z, \end{equation}\]
    • \(F(t\mid Z)=1- S(t\mid Z)\)
    • \(\log\{x/(1-x)\}\): Proportional odds
    • \(\log(-\log(1 - x))\): Proportional hazards (Cox)

Software: timereg::prop.odds()

  • Basic syntax for semiparametric PO model
library(timereg)
# Fit a semiparametric proportional odds model
obj <- prop.odds(Event(time, status) ~ covariates)
  • Input
    • Event(time, status) ~ covariates: similar to Surv(time, status) ~ covariates in coxph()
  • Output: an object of class cox.aalen
    • obj$gamma: \(\hat\beta\); obj$var.gamma: \(\hat\var(\hat\beta)\)
    • obj$cum: matrix containing \(t\) and \(\exp\{\hat h_0(t)\}\)
    • summary(obj): summarizes regression results

PO: German Breast Cancer (I)

  • Semiparametric PO model
    • Hormone reduces odds of early relapse/death by \(1-\exp(-0.522)=40.7\%\) (\(p\)-value 0.002)
# Fit a PO model
obj <- prop.odds(Event(time, status) ~ hormone + meno + age + size + 
                   grade + nodes + prog + estrg, data = df)
# print out summary
summary(obj)
#              Coef.  SE       z      P-val   lower2.5% upper97.5%
# hormone2 -0.52200 0.17000  -3.0800 2.08e-03 -0.855000   -0.18900
# meno2     0.49000 0.24300   1.9100 5.66e-02  0.013700    0.96600
# age      -0.02240 0.01280  -1.7500 8.09e-02 -0.047500    0.00269
# size      0.01150 0.00611   1.7800 7.57e-02 -0.000475    0.02350
# ...

PO: German Breast Cancer (II)

 # Plot baseline cumulative odds
 plot(stepfun(t, c(0, base_odds)), do.points = FALSE, lwd = 2,
      xlim=c(0,80), ylim=c(0,1.4), frame.plot = FALSE,
      ylab="Baseline cumulative odds", xlab="Time (months)", main ="")

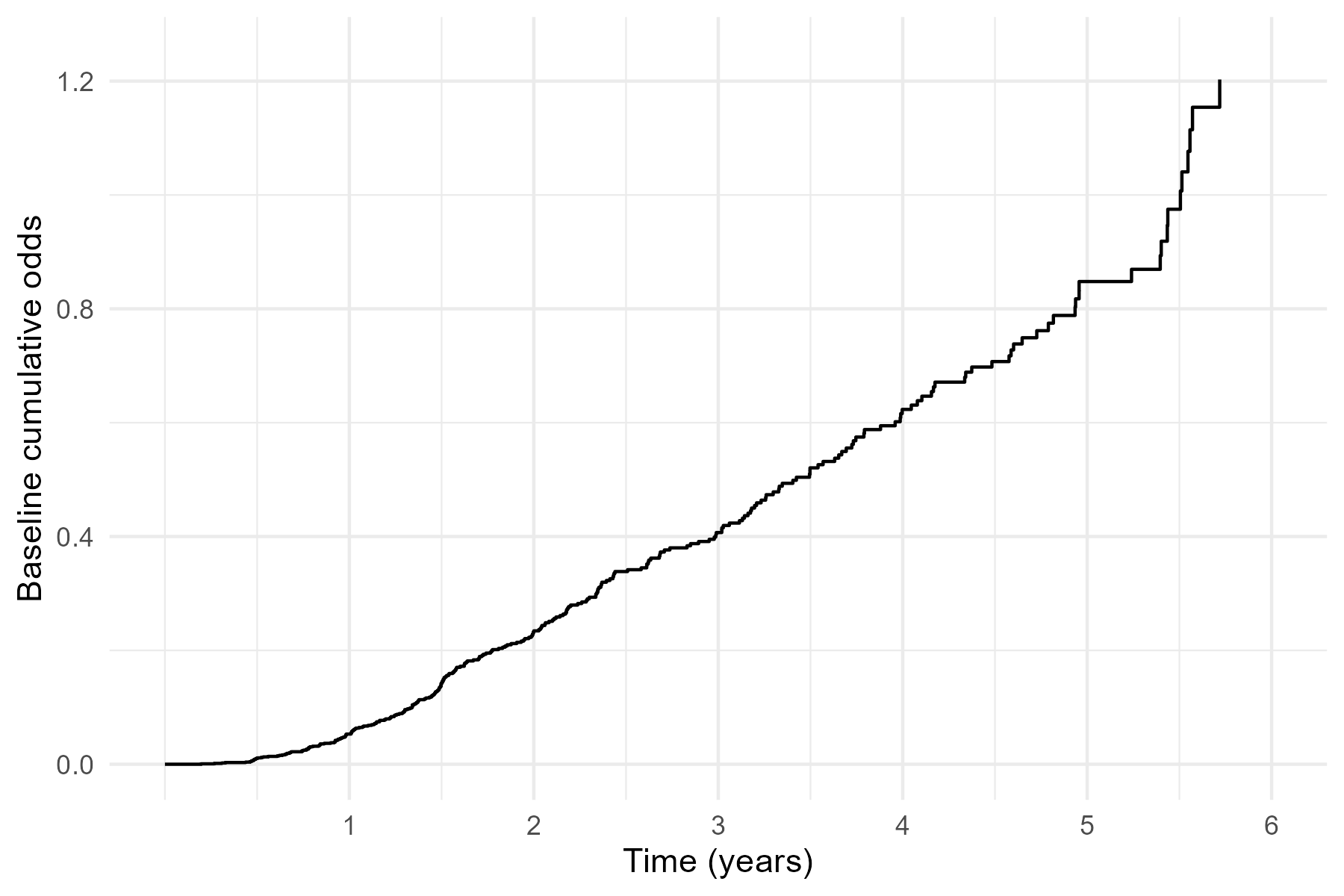
Accelerated Failure Time (AFT) Model

Model Specification

  • Log-linear model \[\begin{equation}\label{eq:non_haz:aft} \log T=\beta^\T Z + \epsilon, \hspace{10mm} \epsilon\indep Z, \end{equation}\]
    • \(\epsilon\): random error with unknow distribution
    • \(T=\exp(\beta^\T Z)\exp(\epsilon)\): multiplicative covariate effects on \(T\)
      • \(Z\) changes survival time by \(\exp(\beta^\T Z)\) fold
    • Accelerated failure time (AFT): with \(S_\epsilon(t)=\pr\{\exp(\epsilon) > t\}\) \[\begin{align*} S(t\mid Z) &=\pr\left\{\exp(\beta^\T Z)\exp(\epsilon) > t\mid Z\right\}\\ & = S_\epsilon\left\{\exp(-\beta^\T Z)t\right\} \end{align*}\]
      • Accelerates time course by a factor of \(\exp(\beta^\T Z)\)

Parametric vs Semiparametric

  • Parametric AFT
    • \(\exp(\epsilon)\sim\) Weibull, log-normal, log-logistic, etc
    • Simplifies estimation \(\to\) MLE
    • Weibull AFT model \(\Leftrightarrow\) Weibull PH model (only distribution with this equivalency)
  • Semiparametric AFT
    • \(\exp(\epsilon)\sim\) nonparametric distribution
    • Buckley-James estimator \[ \mbox{Least squares} \stackrel{\rm iterate}{\longleftrightarrow} \mbox{Imputing censored values} \]

Software: aftgee::aftgee()

  • Basic syntax for semiparametric AFT model
library(aftgee)
# Fit a semiparametric AFT model
 obj <- aftgee(Surv(time,status) ~ covariates)
  • Input
    • Surv(time,status) ~ covariates: same formula as in coxph()
  • Output: an object of class aftgee
    • obj$coef.res: \(\hat\beta\)
    • obj$var.res: \(\hat\var(\hat\beta)\)
    • summary(obj): summarizes regression results

AFT: German Breast Cancer

  • Semiparametric AFT model
    • Hormone increases relapse-free survival time by \(\exp(0.320) = 1.38\) fold (\(p\)-value 0.001)
# Fit an AFT model
set.seed(123)  # SE is based on resampling
obj <- aftgee(Surv(time, status) ~ hormone + meno + age + size + grade + 
                nodes + prog + estrg, data = df,
                B = 500) # Number of resamples
# print out summary
summary(obj)
#             Estimate StdErr z.value p.value    
# (Intercept)    4.262  0.410   10.40  <2e-16 ***
# hormone2       0.320  0.092    3.47   0.001 ***
# meno2         -0.270  0.148   -1.82   0.068 .  
# age            0.013  0.007    1.69   0.092 .  
# size          -0.006  0.003   -1.89   0.059 .  
# ...

Conclusion

Notes

  • Pseudo-value approach to RMST regression \[ \hat{\mu}_i(\tau) = n \hat{\mu}(\tau) - (n - 1) \hat{\mu}^{(-i)}(\tau) \]
    • \(\hat{\mu}^{(-i)}(\tau)\): RMST without \(i\)-th observation
    • Regress \(\hat{\mu}_i(\tau)\) on \(Z_i\)
    • pseudo package
  • Cox–Aalen model \[ \lambda(t \mid Z) \;=\; \lambda_0(t) \exp\left(\gamma^\T Z_{(1)}\right) + \beta(t)^\T Z_{(2)} \]
    • Multiplicative hazards for \(Z_{(1)}\), additive hazards for \(Z_{(2)}\)
    • timereg::cox.aalen()

Summary (I)

  • \(\tau\)-RMST
    • Difference/ratio in survival time by time \(\tau\)
    • Two-sample and regression
    • survRM2::rmst2()
  • Additive hazards
    • Difference in risk (attributable risk)
    • addhazard::ah() (semiparametric: constant difference)
    • timereg::aalen() (nonparametric: time-varying difference)

Summary (II)

  • Proportional odds
    • Odds ratio for an early event
    • timereg::prop.odds()
  • Accelerated failure time
    • Ratio in survival time
    • aftgee::aftgee() (semiparametric: unspecified error distribution)
    • survival::survreg() (parametric error distribution)