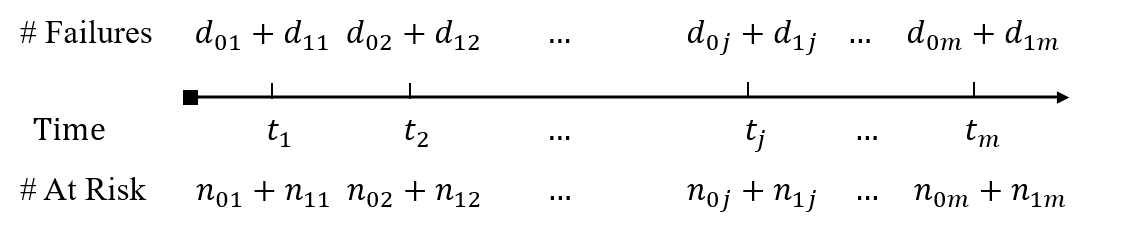Applied Survival Analysis

Chapter 3 - Nonparametric Estimation and Testing

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Nelsen–Aalen estimator of cumulative hazard
  2. Kaplan–Meier estimator of survival function
  3. Log-rank test and variations
  4. Analysis of the German Breast Cancer study

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\]

Nelsen–Aalen Estimator

Nonparametric Approach

  • Motivation
    • Naive empirical distribution biased with censoring
    • Parametric models constrained
      • Weibull model \(\to\) monotone risk
  • Nonparametric inference
    • Estimation of \(S(t)=\pr(T >t)\)
    • Comparison of survival function between groups
  • Discrete hazard: a useful tool

Discrete Hazard: Set-up

  • Observed data \[(X_i, \delta_i)\,\, (i=1,\ldots, n)\]
    • \(0<t_1<\cdots<t_m\): unique observed event (failure) times (the \(X_i\) with \(\delta_i =1\))
    • \(d_j\): number of observed failures at \(t_j\)
    • \(n_j\): number of subjects at risk \(t_j\) (those with \(X_i\geq t_j\))
      • \(n_{j-1} - n_j\): number of failures and censorings in \([t_{j-1}, t_j)\)

Discrete Hazard: Definition

  • Counting process notation \[d_j = \sum_{i=1}^n \dd N_i(t_j)\, \mbox{ and }\,\, n_j = \sum_{i=1}^n I(X_i \geq t_j)\]
  • Discretize distribution at observed event times \[t_1<t_2<\cdots<t_m\]
    • Discrete hazard \[\dd\Lambda(t_j)=\pr(t_j \leq T < t_j+\dd t\mid T\geq t_j)=\pr(T = t_j\mid T\geq t_j)\]
      • \(\dd\Lambda(t)\equiv 0\) otherwise

Nelsen–Aalen Estimator (I)

  • Recall in Chapter 2…\[\begin{align} E\{\dd N(t)\mid X\geq t\}&=\frac{\pr\{\dd N^*(t)=1, C\geq t\}}{\pr(T\geq t, C\geq t)} \notag\\ &=\frac{\pr\{\dd N^*(t)=1\}\pr(C\geq t)}{\pr(T\geq t)\pr(C\geq t)} \notag\\ &=E\{\dd N^*(t)\mid T\geq t\}\notag\\ &=\dd\Lambda(t), \end{align}\]

    • So \[\dd\Lambda(t_j) = E\{\dd N(t_j)\mid X\geq t_j\}=\frac{E\{\dd N(t_j)\}}{\pr(X\geq t_j)}\]

Nelsen–Aalen Estimator (II)

  • Motivates empirical estimator \[\begin{align} \dd\hat\Lambda(t_j) & = \frac{d_j}{n_j} = \frac{\sum_{i=1}^n \dd N_i(t_j)}{\sum_{i=1}^n I(X_i\geq t_j)}\\ &=\mbox{proportion of failures among those at risk} \end{align}\]
  • Cumulative hazard \[ \hat\Lambda(t)=\sum_{j:t_j\leq t}\frac{d_j}{n_j} =\int_0^t\frac{\sum_{i=1}^n \dd N_i(u)}{\sum_{i=1}^n I(X_i\geq u)} \]
    • Nelsen–Aalen estimator
    • A step function (starting from 0) that jumps \(d_j/n_j\) at \(t_j\) \((j=1,\ldots, m)\)

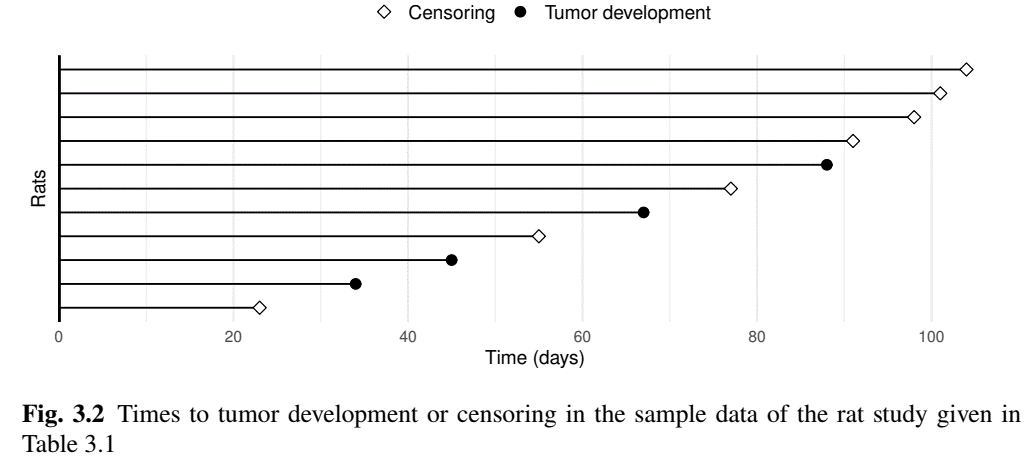
Example: Rat Carcinogen Study (I)

  • Carcinogenicity study: 100 rats treated with a drug
    • Followed for tumor development

Example: Rat Carcinogen Study (II)

  • Follow-up plot (sub-sample)

Example: Rat Carcinogen Study (III)

  • “Hand” calculations

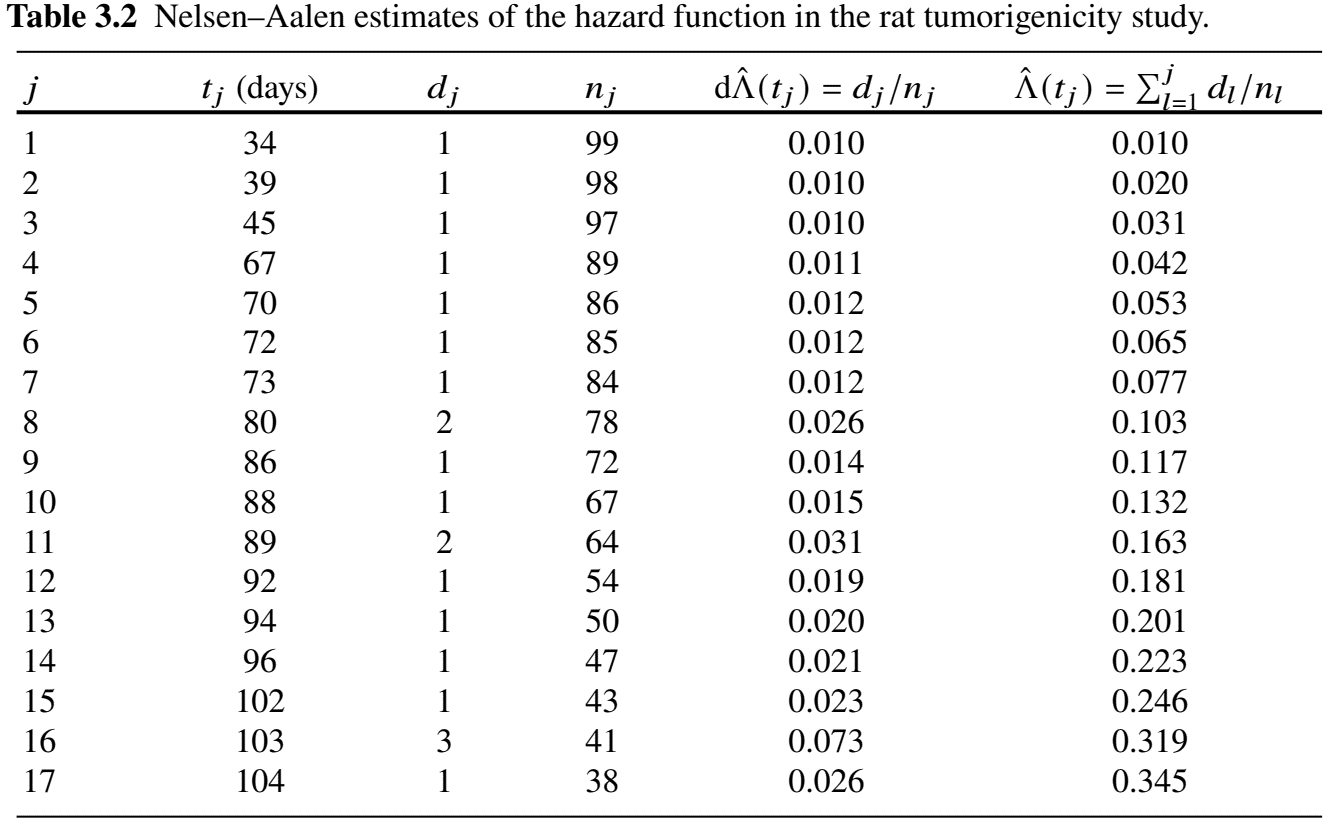
Example: Rat Carcinogen Study (IV)

  • Visualization

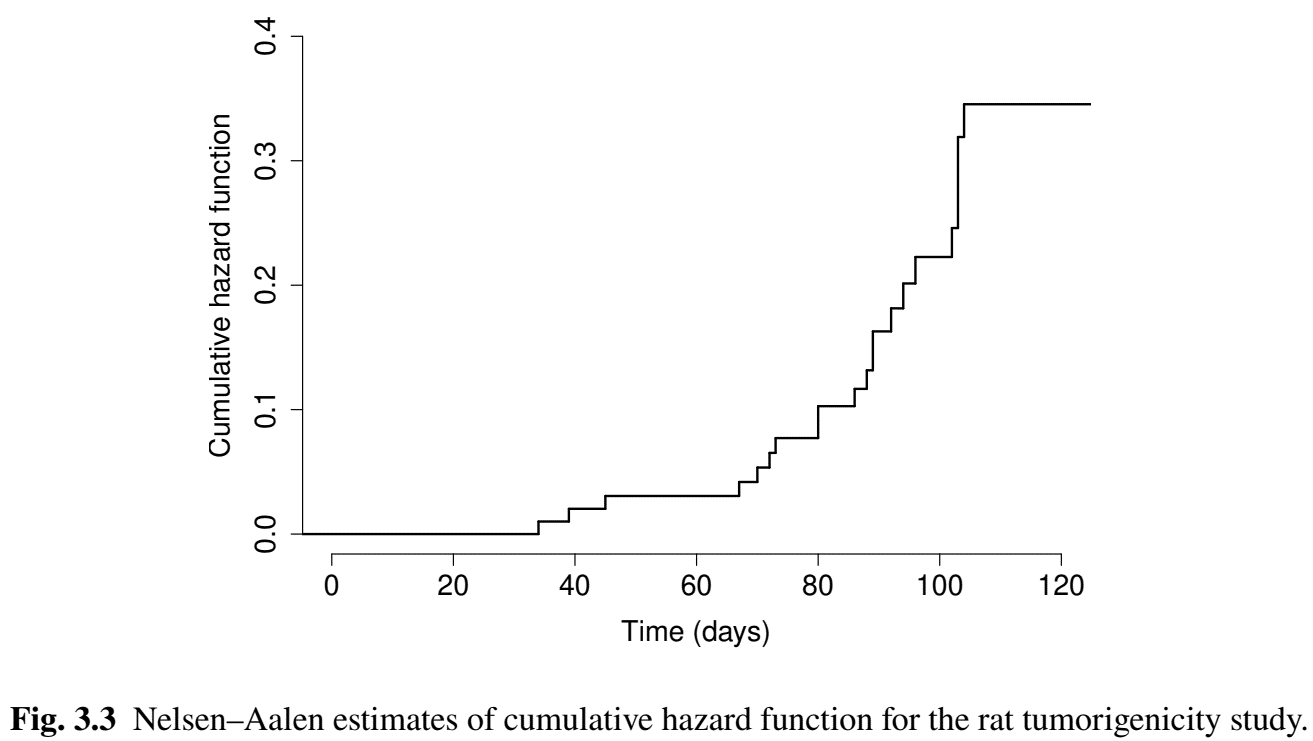
Kaplan–Meier Estimator

From Hazard to Survival

  • Continuous relationship \[ \tilde S(t)=\exp\left\{-\hat\Lambda(t)\right\} \]
  • Discrete relationship (more general and intuitive)

Progressive Conditioning

  • Surviving past \(t_j\): step by step \[\begin{align*} S(t_j)&=\pr(T>t_j)\\ &=\pr(T>t_1)\pr(T>t_2\mid T>t_1)\cdots\pr(T>t_j\mid T>t_{j-1})\\ &=\pr(T>t_1\mid T\geq t_1)\pr(T>t_2\mid T\geq t_2)\cdots\pr(T>t_j\mid T\geq t_j)\\ &=\prod_{l=1}^j\pr(T>t_l\mid T\geq t_l), \end{align*}\]
  • Overall \[\begin{equation*} S(t)=\prod_{j:t_j\leq t}\pr(T>t_j\mid T\geq t_j) \end{equation*}\]

Kaplan–Meier Estimator

  • Each conditional survival \[ \pr(T>t_j\mid T\geq t_j) = 1-\pr(T=t_j\mid T\geq t_j) = 1-\dd\Lambda(t_j) \]
  • Plug-in Nelsen–Aalen \[\begin{equation} \hat S(t)=\prod_{j:t_j\leq t}\{1-\dd\hat\Lambda(t_j)\}=\prod_{j:t_j\leq t}(1-d_j/n_j) \end{equation}\]
    • Kaplan–Meier (product-limit) estimator
    • Reduces to empirical survival in the absence of censoring
    • Adjusts for censoring by updating number at risk \(t_j\) over time

Kaplan–Meier Estimator: Variance (I)

  • \(\var\{\hat S(t)\}\)?

    • Log-transform: product \(\to\) sum \[ \log\hat S(t)=\sum_{j:t_j\leq t}\log(1-d_j/n_j) \]

    • Delta method\(^*\) \[ \hat\var\{\hat S(t)\}=\hat S(t)^2\hat\var\{\log\hat S(t)\}, \]

Delta Method

If approximately \(S_n \sim N(\mu, \sigma^2)\), then approximately \(g(S_n) \sim N\left\{g(\mu), \dot g(\mu)^2\sigma^2\right\}\), where \(\dot g(\mu)=\dd g(\mu)/\dd\mu\).

Kaplan–Meier Estimator: Variance (II)

  • \(\var\{\log\hat S(t)\}\)?
    • With the \(n_j\) fixed, the \(d_j\) are independent (different subjects) \[\begin{align} \hat{\rm var}\{\log\hat S(t)\}&=\sum_{j:t_j\leq t}\hat{\rm var}\left[\log\{1-d_j/n_j\}\right]\notag\\ &\approx \sum_{j:t_j\leq t}\frac{n_j^2}{(n_j-d_j)^2}\hat{\rm var}(d_j/n_j)\tag{Delta method}\\ &=\sum_{j:t_j\leq t}\frac{d_j}{n_j(n_j-d_j)}, \end{align}\]
    • Last equality: variance of binomial proportion \[ \hat{\rm var}(d_j/n_j)=(d_j/n_j)(1-d_j/n_j)/n_j \]

Kaplan–Meier Estimator: Variance (III)

  • Variance of KM \[\begin{equation}\label{eq:km:greenwood} \hat\var\{\hat S(t)\}=\hat S(t)^2\sum_{j:t_j\leq t}\frac{d_j}{n_j(n_j-d_j)} \end{equation}\]

    • Greenwood’s formula

  • Naive 95% confidence interval (CI) \[\begin{equation}\label{eq:km:ci_plain} \left[\hat S(t)-1.96\hat\se\{\hat S(t)\}, \hat S(t)+1.96\hat\se\{\hat S(t)\}\right] \end{equation}\]

    • May contain values outside \([0, 1]\)
    • Bounded quantity approximated by unbounded (normal) distribution

Kaplan–Meier Estimator: CI

  • Log-log transformed CI

    • Transform \(\zeta(t)=\log\{-\log S(t)\} \in \mathbb R\)

    • CI for \(\zeta(t)\) \[\begin{equation} \left[\hat\zeta(t)-1.96\hat\se\{\hat\zeta(t)\},\hat\zeta(t)+1.96\hat\se\{\hat\zeta(t)\}\right] \end{equation}\]

    • Transform the bounds back to \(S(t)\) \[ \left[\hat S(t)^{\exp[1.96\hat\se\{\hat\zeta(t)\}]}, \hat S(t)^{\exp[-1.96\hat\se\{\hat\zeta(t)\}]}\right] \subset [0, 1] \]

    • Remains to calculate \(\hat\se\{\hat\zeta(t)\}\) by delta method (Exercise)

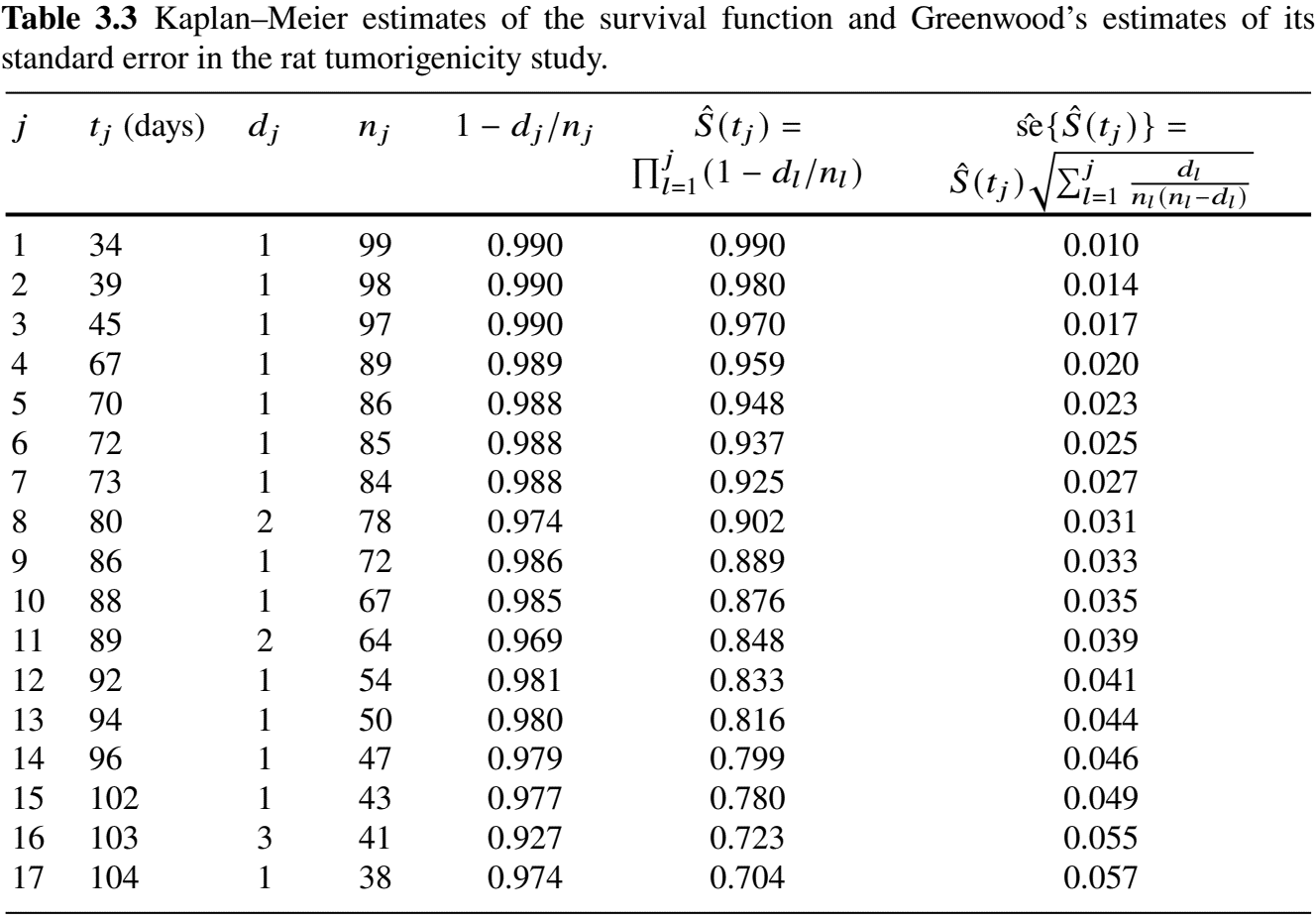
Example: Rat Carcinogen Study (V)

  • “Hand” calculations

Software: survival::survfit() (I)

  • Basic syntax for fitting KM curve
 # df: data frame; time: X; status: delta
obj <- survfit(Surv(time, status) ~ 1, data = df, 
               conf.type = "log-log")
  • Input
    • Surv(time, status) ~ 1: fit curve to a homogeneous sample
      • Surv(time, status) ~ group: fit curve to each level of group
    • data = df: input data frame df
    • conf.type = "log-log": log-log transformation for CI
      • "log": default log transformation
      • "plain": naive CI

Software: survival::survfit() (II)

  • Output: a surfit object containing KM estimates
    • Call summary() and plot()
    • summary(obj): a list containing
      • time: \(t_j\) \((j=1,\ldots, m)\)
      • surv: \(\hat S(t_j)\)
      • n.risk: \(n_j\)
      • n.event: \(d_j\)
      • std.err: \(\hat\se\{\hat S(t_j)\}\)
      • ...

Software: gtsummary::tbl_survfit()

  • Customizable, publication-ready table
    • Based on survfit() results
# install.packages("gtsummary")
library(gtsummary)
# A single-group KM model
obj <- survfit(Surv(time, status) ~ 1, data = df)

# Summaries at specific times
tbl_surv <- tbl_survfit(
  x = obj,                         # Provide the fitted survfit object
  times = seq(40, 100, by = 20),   # Time points for survival rates
  label_header = "{time} days"     # Column label: "xx days"
)

# Print out the table
tbl_surv

Software: ggsurvfit::ggsurvfit()

  • Enhanced KM plot
    • Powered by ggplot2
# install.packages("ggsurvfit")
library(ggsurvfit)
obj <- survfit(Surv(time, status) ~ 1, data = df)

# Create a KM plot with confidence intervals and an at-risk table
ggsurvfit(obj) +
  add_confidence_interval() + # Shaded 95% CI region
  add_risktable() +           # Show risk table
  scale_x_continuous(breaks = seq(0, 100, by = 20)) + # X-axis breaks
  ylim(0, 1) +                # Y-axis limits
  labs(
    x = "Time (days)",
    y = "Tumor-free probabilities"
  ) +
  theme_minimal()

Example: Rat Carcinogen Study (VI)

  • Data frame: rats.rx
    • Check with Table 3.3
obj <- survfit(Surv(time, status) ~ 1, data = rats.rx, 
               conf.type = "log-log")
summary(obj)
# Call: survfit(formula = Surv(time, status) ~ 1, data = rats.rx, 
#               conf.type = "log-log")
# 
# time n.risk n.event survival std.err lower 95% CI upper 95% CI
#   34     99       1    0.990  0.0100        0.930        0.999
#   39     98       1    0.980  0.0141        0.922        0.995
#   45     97       1    0.970  0.0172        0.909        0.990
#   67     89       1    0.959  0.0202        0.894        0.984
#   70     86       1    0.948  0.0228        0.879        0.978
#   ...

Example: Rat Carcinogen Study (VII)

  • Plot the survival function (with 95% CI)
    • Base plot()
# plot the estimated survival function
plot(obj, ylim = c(0,1), xlim = c(0, 100), lwd = 2, frame.plot = FALSE,
     xlab = "Time (days)", ylab = "Tumor-free probabilities", main = "")

legend(1, 0.2, c("Kaplan-Meier curve", "95% Confidence limits"),
       lty = 1:2, lwd = 2)

Example: Rat Carcinogen Study (VIII)

  • Result

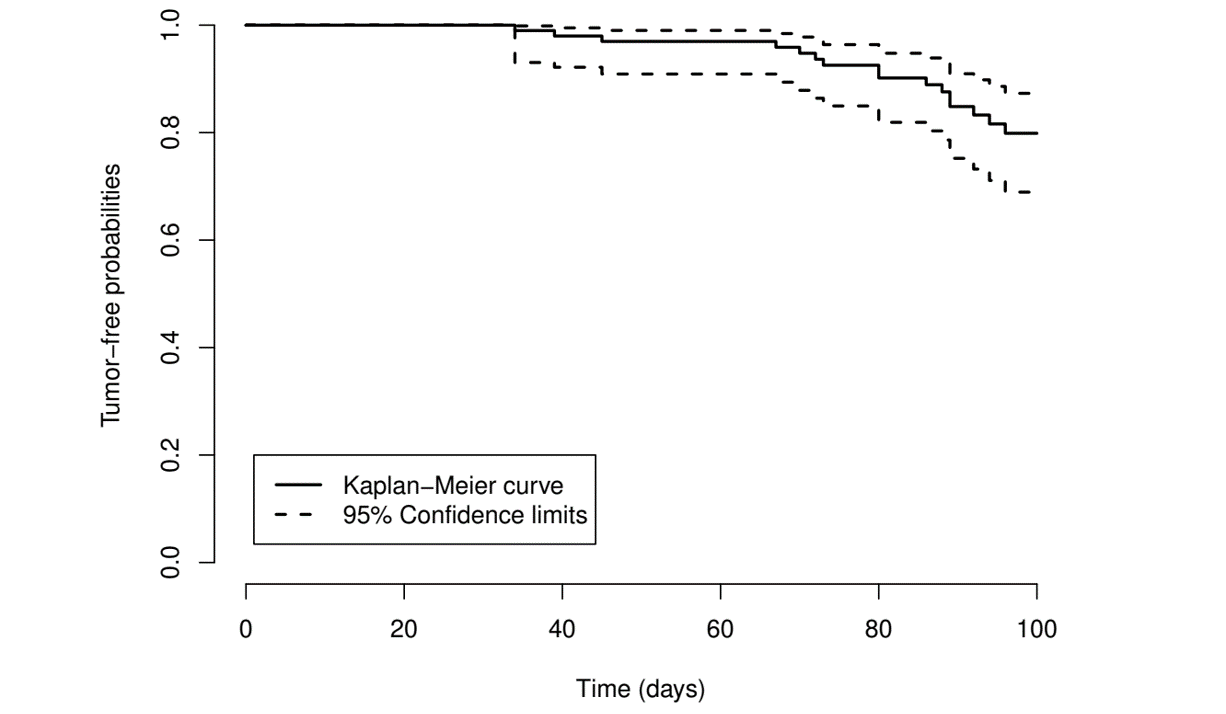
Log-Rank Test

Comparing Survival Rates

  • Motivation: compare event rate across groups for treatment/exposure effect
  • Example
    • Rat study: 100 treated (analyzed) vs 200 untreated for tumor incidence
    • GBC study: hormone vs non-hormone treatments for (relapse-free) survival
  • Hypothesis \[\begin{equation}\label{eq:km:null} H_0: S_1(t)=S_0(t) \mbox{ for all } t. \end{equation}\]
    • \(S_a(t) =\) survival function of \(T\) in group \(a\) (\(1\): treatment; \(0\): control)

Two-Group Comparison: Set-up

  • Observed data \[\begin{equation} \{(X_{1i},\delta_{1i}): i=1,\ldots, N_1\} \mbox{ and } \{(X_{0i},\delta_{0i}): i=1,\ldots, N_0\}, \end{equation}\]
    • \((X_{ai},\delta_{ai})\) \((i=1,\ldots, N_a)\): a random sample of \((X,\delta)\) in group \(a\)
    • \(n_{1j}\), \(n_{0j}\): numbers at risk in groups 1 and 0 at \(t_j\) (totaling \(n_j = n_{1j} + n_{0j}\) at risk)
    • \(d_{1j}\), \(d_{0j}\): numbers of events in groups 1 and 0 at \(t_j\) (totaling \(d_j = d_{1j} + d_{0j}\) events)

Two-Group Comparison: Contingency

  • Fixing \(d_j\) (total # uninformative of group difference)

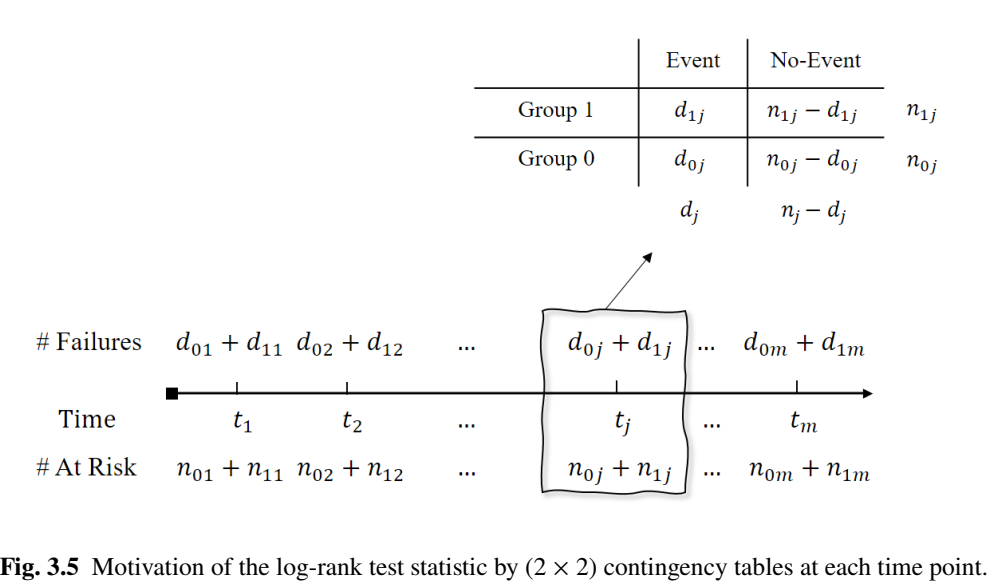
Two-Group Comparison: Log-rank (I)

  • Contingency table \((2\times 2)\)
    • \(H_0\): No association between event occurence vs group affiliation
    • Event occurs in proportion to number at risk \[\begin{align} R_j&=d_{1j}-d_j\frac{n_{1j}}{n_j}\\ &=\mbox{(Observed events)} - \mbox{(Expected events)} \end{align}\]
    • \(R_j > 0\): higher incidence in treatment; \(R_j < 0\): higher incidence in control
    • \(E(R_j\mid d_j, n_{1j}, n_{0j})\stackrel{H_0}{=}0\)
    • \(\var(R_j\mid d_j, n_{1j}, n_{0j})\stackrel{H_0}{=:} V_j\) by hypergeometric distribution

Two-Group Comparison: Log-rank (II)

  • Testing overall incidence \[\begin{equation}\label{eq:km:logrank_stat} S_{N_1,N_0}=\frac{(\sum_{j=1}^m R_j)^2}{\sum_{j=1}^m V_j}\stackrel{H_0}{\sim} \chi_1^2 \end{equation}\]
    • \(\hat\var(\sum_{j=1}^m R_j)=\sum_{j=1}^m V_j\) by conditioning (martingale) arguments
      • Uncorrelated increments
    • Reject \(H_0\) if \[S_{N_1,N_0}>\chi_1^2(1-\alpha)\]
      • \(\chi_1^2(1-\alpha)\) is the \(100(1-\alpha)\)th percentile of \(\chi_1^2\)
    • Log-rank test (with significance level \(\alpha\))

Two-Group Comparison: Log-rank (III)

  • Alternative hypothesis \[\begin{equation}\label{eq:km:logrank_alter} H_A: \lambda_1(t)\leq\lambda_0(t)\mbox{ for all } t \mbox{ with strict inequality for some }t \end{equation}\]
    • Ordered hazards: treatment consistently lowers risk over time compared to control (or vice versa) \[\pr\left\{S_{N_1,N_0}>\chi_1^2(1-\alpha)\right\}\stackrel{H_A}{\to} 1 \mbox{ as } n\to\infty\]
    • \(\sum_{j=1}^m R_j =\) Weighted difference of group-specific Nelsen–Aalen estimates of hazard functions (Section 3.2.2)
    • Crossing hazards \(\to\) weak power

Log-Rank Extension: Multiple Groups

  • \(K\) groups \((k = 0, 1, \ldots, K-1)\) \[\begin{equation}\label{eq:km:logrank_mult} \gamma=\sum_{j=1}^m\left(d_{1j}-d_j\frac{n_{1j}}{n_j},d_{2j}-d_j\frac{n_{2j}}{n_j},\ldots, d_{K-1,j}-d_j\frac{n_{K-1,j}}{n_j}\right)^{\rm T} \end{equation}\]
    • \(t_1<\cdots<t_m\): unique event times pooled across \(K\) groups
    • \(d_{kj}, n_{kj}\): numbers of failed and at-risk subjects in group \(k\) at \(t_j\)
    • Test statistic \[ \gamma^{\rm T}\var(\gamma)^{-1}\gamma\stackrel{H_0}{\sim}\chi_{K-1}^2 \]
    • Alternative hypothesis: exist two groups with ordered hazards

Log-Rank Extension: Stratification

  • Stratification: compare groups only within same stratum
    • Race/ethnicity, sex, age group, study center
    • Adjust for confounder
    • Statistical efficiency
  • Test statistic
    • Calculate and aggregate stratum-specific \(\sum_{j=1}^m R_j\)
    • Alternative hypothesis: ordered hazards (same order) across strata

Log-Rank Extension: Weighting (I)

  • Weight \(w_j\) at time \(t_j\): \[\begin{equation}\label{eq:eq:km:ej_w} \frac{(\sum_{j=1}^{m} w_jR_{j})^2}{\sum_{j=1}^{m} w_j^2V_{j}} \stackrel{H_0}{\sim} \chi_1^2 \end{equation}\]
    • Log-rank: \(w_j\equiv 1\)
    • Gehan: \(w_j = n_j/n\)
    • Harrington-Fleming (HF) \(G^\rho\) family: \(\hat S(t_j-)^\rho\) \((\rho\geq 0)\)
      • \(\hat S(t_j-)\): KM estimate based on pooled sample
      • Extended to \(G^{\rho,\gamma}\) family: \(\hat S(t_j-)^\rho\{1-\hat S(t_j-)\}^\gamma\) \((\rho, \gamma \geq 0)\)

Log-Rank Extension: Weighting (II)

  • Choice
    • Pre-specify to avoid bias
    • Decreasing weights: sensitive to early effects
    • Increasing weights: sensitive to delayed effects
    • Constant weight (default): optimal for proportional hazards alternative \[ H_A^{\rm PH}:\lambda_1(t)=\exp(\theta)\lambda_0(t) \mbox{ for all } t \]

Software: survival::survdiff()

  • Basic syntax for log-rank test
# Log-rank test
survdiff(Surv(time, status) ~ group + strata(str_var), rho)
  • Input
    • Surv(time, status) ~ group: test survival function between levels of variable group
    • strata(str_var): stratified by variable str_var (optional)
    • rho = r: weights \(\hat S(t_j-)^\rho\) with \(\rho=\) r
  • Output: a list containing pvalue (p-value of the test)

Software: gtsummary::tbl_survfit()

  • Multi-group tabulation
library(gtsummary)
# A two-group KM model
obj <- survfit(Surv(time, status) ~ rx, data = rats)

# Summaries at specific times with labeled treatment groups
tbl_surv <- tbl_survfit(
  x = obj,                         # Provide the fitted survfit object
  times = seq(40, 100, by = 20),   # Time points for survival rates
  label_header = "{time} days",    # Column label: "xx days"
  label = list(rx ~ "Treatment")   # Rename 'rx' to 'Treatment'
)

# Print out the table
tbl_surv

Software: ggsurvfit::ggsurvfit()

  • Multi-group KM graphics
library(ggsurvfit)

# Use survfit2 as recommended by ggsurvfit
obj2 <- survfit2(Surv(time, status) ~ rx, data = rats)

# Create a group-specific KM plot with log-rank test p-value
ggsurvfit(obj, linetype_aes = TRUE, linewidth = 1) +  # Use line types 
  add_risktable(                    
    risktable_stats = "n.risk",  # Include only numbers at risk
    theme = list(
      theme_risktable_default(),  # Default risk table theme
      scale_y_discrete(labels = c('Drug', 'Control'))  # Group labels
    )
  ) +  
  theme_classic()

Example: Rat Carcinogen Study (IX)

  • Log-rank test by rx stratified by sex
head(rats)
#   litter rx time status sex
# 1      1  1  101      0   f
# 2      1  0   49      1   f
# 3      1  0  104      0   f
# ...

survdiff(Surv(time, status) ~ rx + strata(sex), data = rats)
# Call:
# survdiff(formula = Surv(time, status) ~ rx + strata(sex), data = rats)
# 
#        N Observed Expected (O-E)^2/E (O-E)^2/V
# rx=0 200       21     28.9      2.16      6.99
# rx=1 100       21     13.1      4.77      6.99
# 
#  Chisq= 7  on 1 degrees of freedom, p= 0.008

Application: German Breast Cancer Study

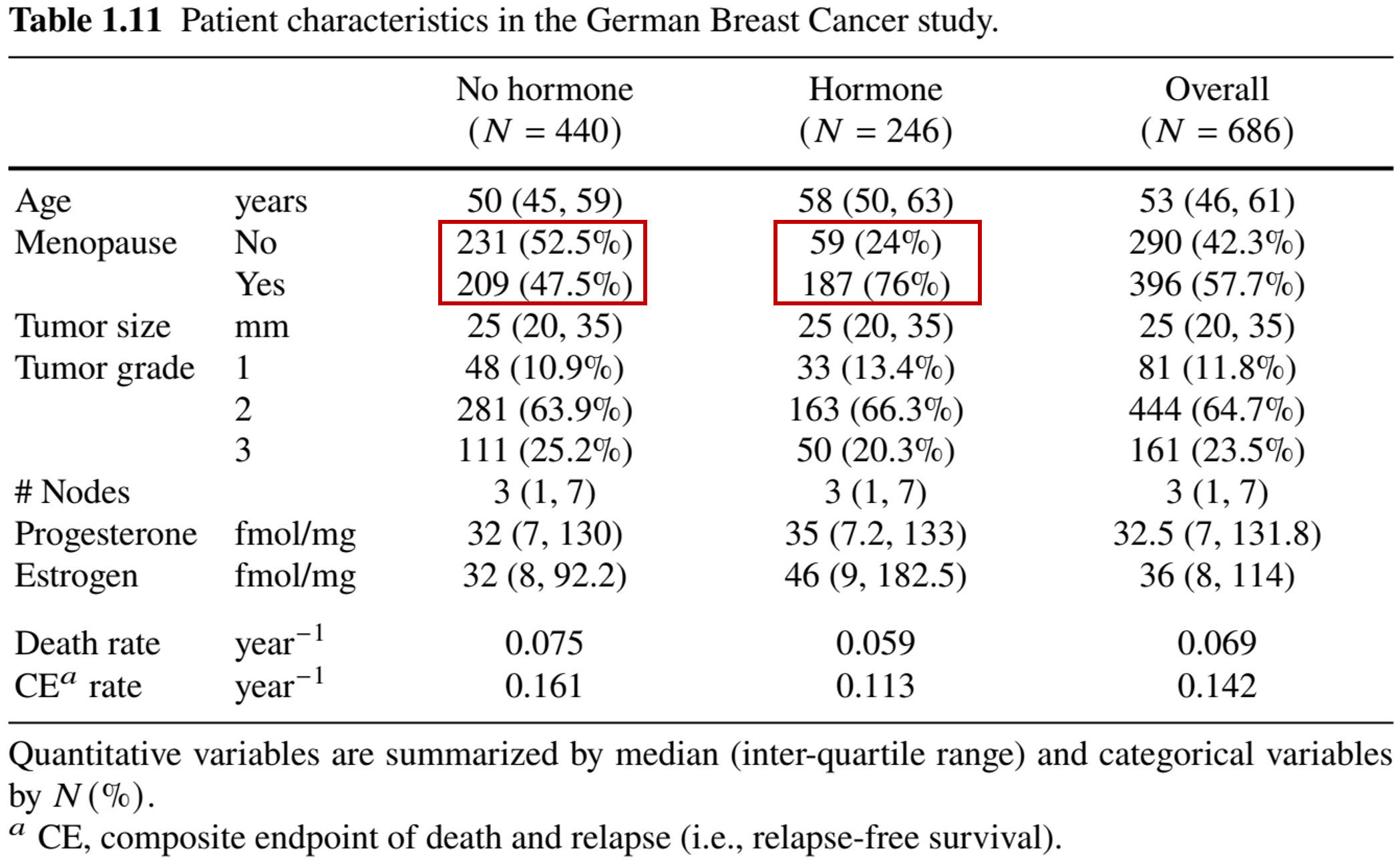
Baseline Characteristics

  • 686 patients with primary node positive breast cancer

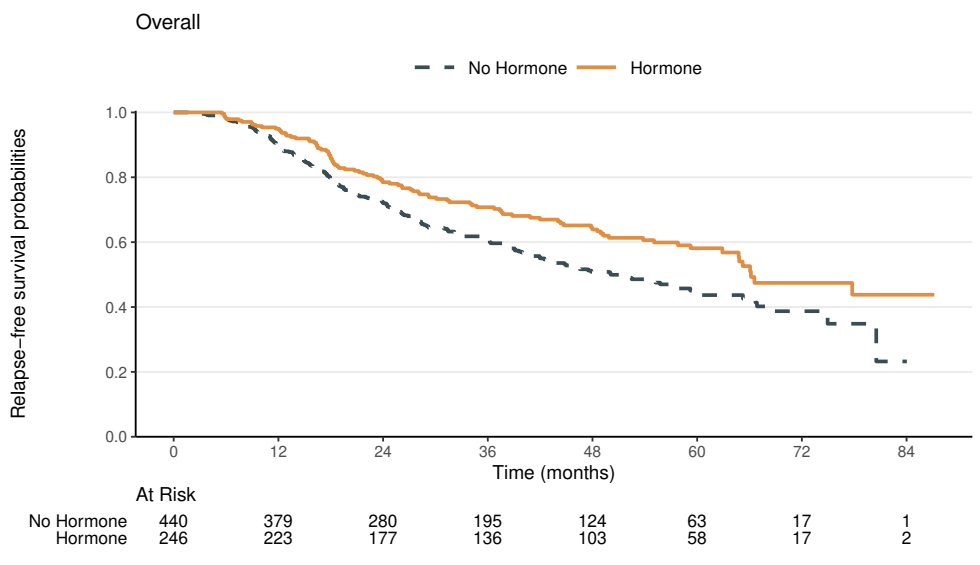
Relapse-Free Survival: Overall

  • Endpoint: the earlier of relapse or death

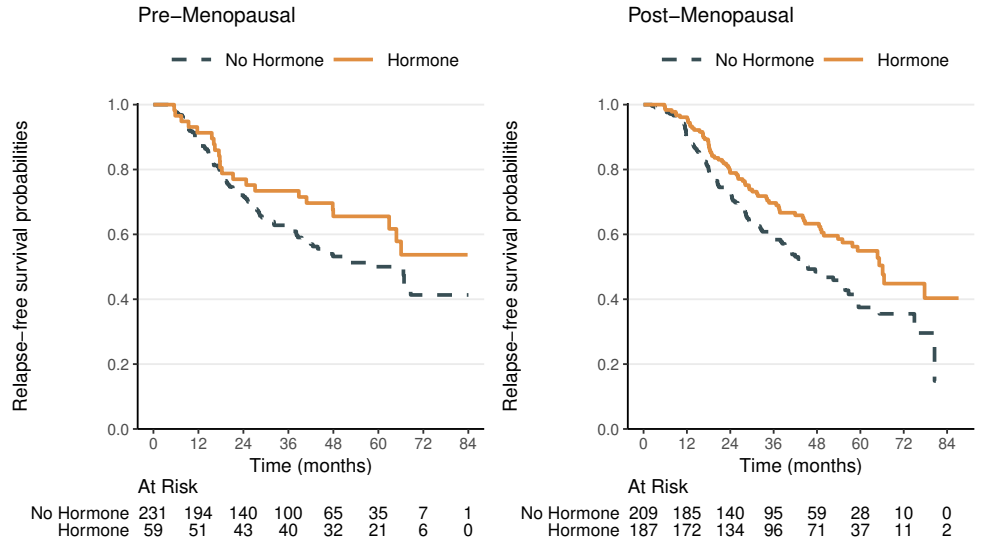
Relapse-Free Survival: Subgroups

  • Menopausal status: pre- vs post-menopausal

Hormone Treatment Effect

  • Hormonal therapy
    • Stratified by menopausal status
## Stratified log-rank test (by menopausal status)
survdiff(Surv(time, status) ~ hormone + strata(meno),
         data = data.CE)
  • Result
    • \(\chi_1^2=\) 9.5 with p-value 0.002
      • Adjusting for menopausal status, hormonal therapy has a highly significant beneficial effect on relapse-free survival in breast cancer patients
    • Unadjusted test result similar

Conclusion

Notes

  • Kaplan and Meier (1958)
    • 60k + citations by Feb 2025
    • Most cited statistical paper of all time
  • Derivation of log-rank
    • Mantel–Haenszel (1959) analysis of \(2\times 2\) contingency tables stratified by \(t_j\)
  • Other tests
    • Gehan npsm::gehan.test()
    • Max-combo nph::logrank.maxtest() (maximum over multiple weighting schemes)

Summary (I)

  • Discrete hazard: \(\dd\Lambda(t_j)= d_j/n_j\)
    • Proportion of failures among those at risk
  • Kaplan–Meier \[\begin{equation} \hat S(t)=\prod_{j:t_j\leq t}\{1-\dd\hat\Lambda(t_j)\}=\prod_{j:t_j\leq t}(1-d_j/n_j) \end{equation}\]
    • survival::survfit():

Summary (II)

  • Log-rank test: multi-group comparison
    • \(K\) groups \(\to\) \(K-1\) degrees of freedom
    • Stratification: adjust for confounding
    • Weighting: optimality depends on effect pattern over time
    • survival::survdiff()
  • Enhanced tabulation and graphics
    • gtsummary::tbl_survfit()
    • ggsurvfit::ggsurvfit()

HW2 (Due Feb 19)

  • Choose one

    • Problem 3.2
    • Problem 3.3

  • Problem 3.19

  • (Extra credit) Choose one

    • Problem 3.15
    • Problems 3.17 and 3.18