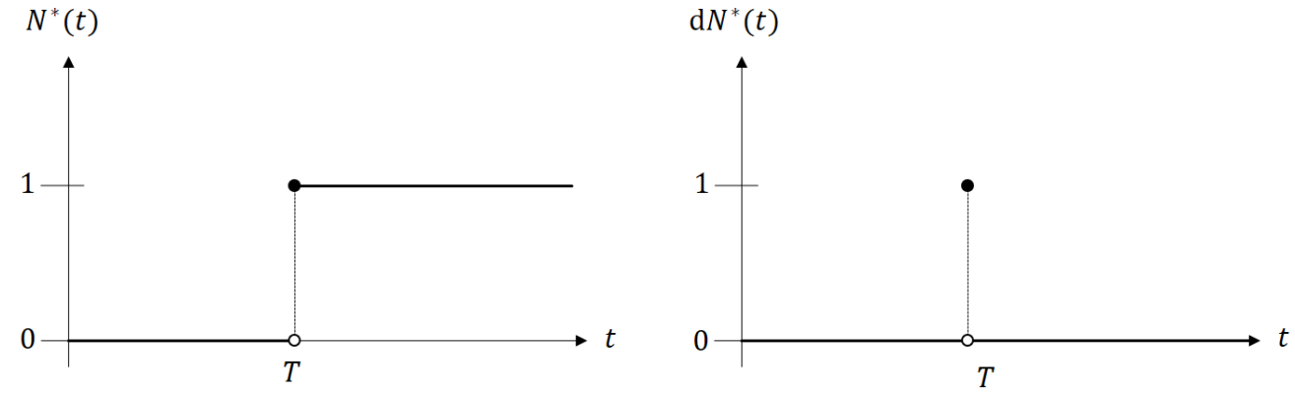Applied Survival Analysis

Chapter 2 - Mathematical Foundations

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Random variable and counting process notations
  2. Likelihood and score functions
  3. Martingale residuals and integrals \[\newcommand{\d}{{\rm d}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\]

Mathematical Notation

Outcome Event: Notation

  • Time to outcome event (latent, w.o. censoring): \(T\)

    • Cumulative distribution function (cdf): \(F(t)={\rm pr}(T\leq t)\)
    • Survival function: \(S(t) = 1- F(t) = {\rm pr}(T > t)\)
    • Density function: \(f(t) = \d F(t)/\d t = - \d S(t)/ \d t\)

  • Leibniz notation

    • \(\d F(t) = f(t)\d t = \pr(t \leq T < t + \d t)\): infinitesimal (marginal) event rate (i.e. incidence) over \([t, t + \d t)\)

Outcome Event: Hazard Function

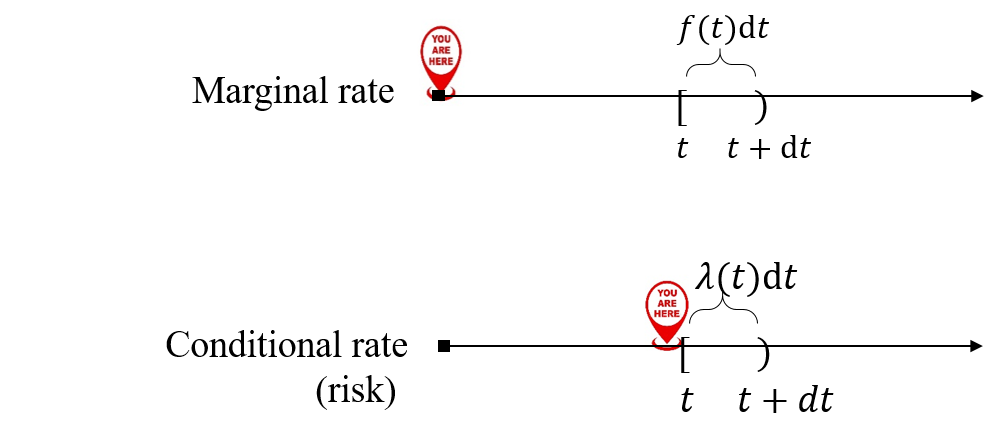
  • Hazard rate: conditional incidence for those currently at risk \[\lambda(t)\dd t=\pr(t\leq T<t+\dd t\mid T\geq t)=\frac{\dd F(t)}{S(t-)}\]

    • So \(\lambda(t) = f(t)/S(t-)\)

  • Density vs hazard functions

Outcome Event: Distributions

  • Conversions

    • \(\lambda(t)\d t = - \d S(t)/S(t -) = -\d\log S(t)\)
    • \(S(t) = \exp\{-\Lambda(t)\}\), where \(\Lambda(t)=\int_0^t \lambda(u)\d u\) (cumulative hazard)

  • Examples

    • Exponential distribution: \(\lambda(t)\equiv \lambda > 0\), \(S(t)=\exp(-\lambda t)\)
      • Constant risk, also β€œmemoryless”: \(\pr(T > t + u\mid T > t) = \pr(T > u)\)
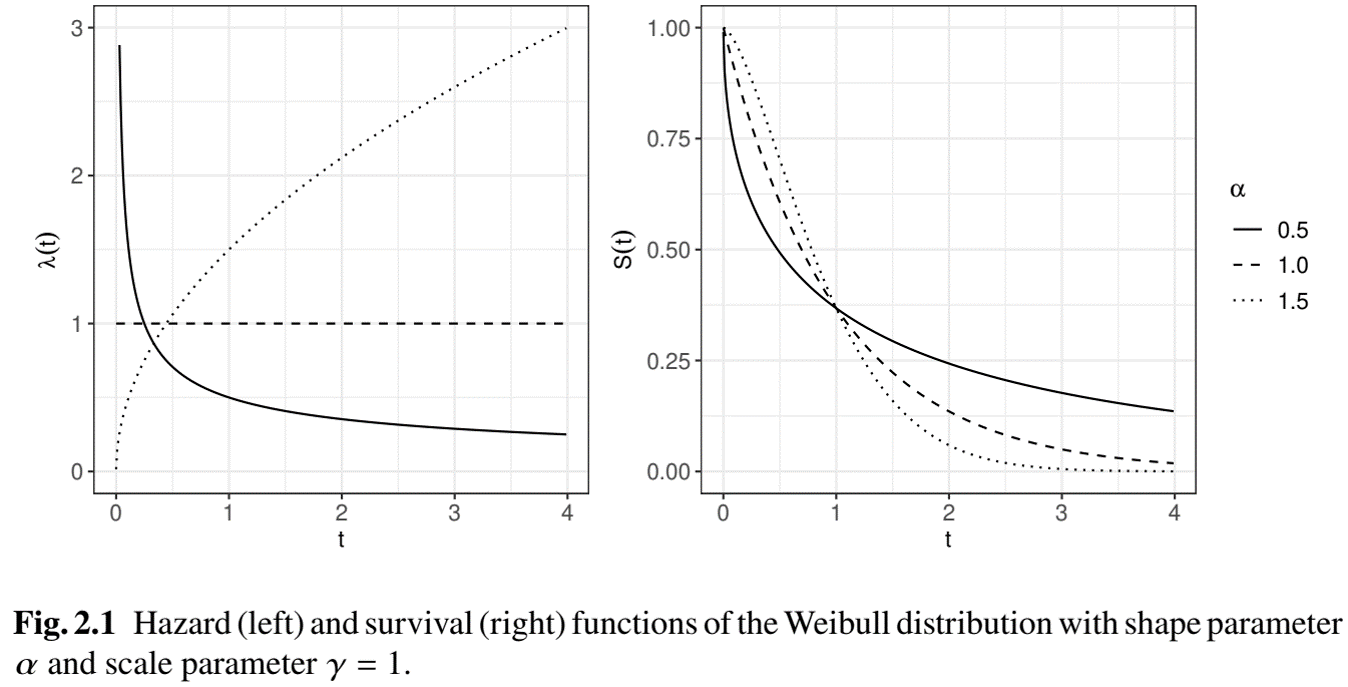
    • Weibull distribution: \(\lambda(t;\alpha,\gamma)=\alpha\gamma^{-\alpha} t^{\alpha-1}\) with \(\gamma, \alpha>0\)
      • \(0 < \alpha < 1\): risk \(\downarrow\) (infant mortality)
      • \(\alpha > 1\): risk \(\uparrow\) (aging effect)
      • \(\alpha = 1\): Exponential (constant risk)
      • \(\gamma\): scale parameter such that \(E(T)\propto \gamma\)

Outcome Event: The Weibull

  • Weibull\((\alpha, \gamma)\)

Outcome Event: Counting Process

  • Definition

    • \(N^*(t)=I(T\leq t)\): number of event (0 or 1) by \(t\) (cumulative)

    • \(\d N^*(t)=N^*(t) - N^*(t-) = I (T=t)\): number of event at \(t\) (incident) \[E\{N^*(t)\} = F(t),\,\,\, E\{\d N^*(t)\} = \d F(t)\] \[E\{\d N^*(t)\mid N^*(t -) = 0\} = E\{\d N^*(t)\mid T\geq t\}=\d\Lambda(t)\]

Observed Data

  • Observed data: \((X, \delta)\)
    • \(X = T\wedge C\): duration of follow-up (time variable) \((a\wedge b = \min(a, b))\)
    • \(\delta = I(T\leq C)\): event indicator (status variable)
    • \(C\): (right) censoring time
  • Observed counting process
    • \(N(t) = I(X\leq t, \delta = 1)\)
    • So \(\d N(t) = \d N^*(t)I(C\geq t)\)
  • Independent censoring assumption

\[C\indep T\]

Likelihood and Score

Likelihood Function

  • Likelihood on a single subject \[p(X, \delta)\propto f(X)^\delta S(X)^{1-\delta}=\lambda(X)^\delta S(X)\]

  • Log-likelihood on a random \(n\)-sample

    • Under a model with parameter \(\theta\): \(\lambda(t) = \lambda(t; \theta)\), \(\Lambda(t) = \Lambda(t; \theta)\) \[\begin{align} l_n(\theta)&= n^{-1}\sum_{i=1}^n\log p(X_i, \delta_i)\\ &=n^{-1}\sum_{i=1}^n\left\{\delta_i\log\lambda(X_i;\theta) -\Lambda(X_i;\theta)\right\}\\ &= n^{-1}\sum_{i=1}^n\left\{\delta_i\log\lambda(X_i;\theta)-\int_0^\infty I(X_i\geq t) \lambda(t;\theta)\dd t\right\} \end{align}\]

Score Function

  • Score function can be derived as \[\frac{\partial}{\partial\theta} l_n(\theta)=n^{-1}\sum_{i=1}^n \left\{\delta_ih(X_i;\theta)-\int_0^\infty h(t;\theta) I(X_i\geq t)\lambda(t;\theta)\dd t\right\}\]
    • where \(h(t;\theta)=\frac{\partial}{\partial\theta}\log\lambda(t;\theta)\) (hazard score function)
    • Solve \(\frac{\partial}{\partial\theta} l_n(\hat\theta)=0\) to obtain maximum likelihood estimator (MLE) \(\hat\theta\)
  • Example: exponential distribution \(\lambda(t; \theta) = \lambda\)
    • \(h(t;\theta) =\lambda^{-1}\)
    • Solving score equation to obtain (in general, use Newton-Raphson algorithm) \[\hat\lambda=\frac{\sum_{i=1}^n\delta_i}{\sum_{i=1}^n X_i}\]

Martingale and Integrals

Stochastic Integration

  • Transformation by some \(h(\cdot)\)

    • \(h(T)\) if \(T\) is observed to lie in \([0, t]\)
    • 0 otherwise

  • Clearly, this is \(\delta I(X\leq t) h(X)\)

  • Compact notation \[\delta I(X\leq t) h(X) = \int_0^t h(u)\dd N(u)\]

    • \(\dd N(u) = 1\) only if \(\delta = 1\) and \(T= u\in[0, t]\)
    • \(\dd N(u) \equiv 0\) otherwise

Stochastic Integration: Examples

  • Log-likelihood \[ l_n(\theta)=n^{-1}\sum_{i=1}^n\left\{\int_0^\infty \log\lambda(t;\theta)\dd N_i(t)-\int_0^\infty I(X_i\geq t)\lambda(t;\theta)\dd t\right\} \]
    • \(N_i(t)= I(X_i\leq t, \delta_i =1)\), i.e., \(N(t)\) on subject \(i\)
  • Score (subject-level) \[ \begin{align} \dot l(\theta)&=\int_0^\infty h(t;\theta)\dd N(t)-\int_0^\infty h(t;\theta) I(X\geq t)\dd\Lambda(t;\theta)\\ &=\int_0^\infty h(t;\theta)\left\{\dd N(t)-I(X\geq t)\dd\Lambda(t;\theta)\right\} \end{align} \]

Martingale: Definition

  • In previous score example, \[\dot l(\theta) = \int_0^\infty h(t;\theta)\dd M(t;\ \theta)\]
    • \(\dd M(t;\theta)=\dd N(t) - I(X\geq t)\dd\Lambda(t;\theta)\)
  • General martingale residual \[ \begin{align} \dd M(t)&=\dd N(t) - I(X\geq t)\dd\Lambda(t)\\ &= \dd N(t) - E\{\dd N(t)\mid\mbox{Data prior to }t\} \end{align} \]
    • So \(E\{\dd M(t)\mid\mbox{Data prior to }t\}=0\)

Martingale: Construction

  • Data observed up to \(t\) \[ \mathcal H(t) =\{N(u), N_C(u):0\leq u\leq t\} \]
    • \(\mathcal H(t-) =\) Data prior to \(t\)
  • Show \[E\{\dd N(t)\mid\mathcal H(t-)\} = I(X\geq t)\dd\Lambda(t)\]
    • How can the past influence the current incidence (risk)?
    • Only through the at-risk status \({X\geq t}\)

Martingale: Derivation

  • Consider not-at-risk \((X < t)\) and at-risk \((X\geq t)\) separately: \[ \begin{align} E\{\dd N(t)\mid\mathcal H(t-)\}&=I(X<t)E\{\dd N(t)\mid X<t, \mathcal H(t-)\}\notag\\ &\hspace{15mm}+I(X\geq t)E\{\dd N(t)\mid X\geq t, \mathcal H(t-)\}\notag\\ & = 0 + I(X\geq t)E\{\dd N(t)\mid X\geq t\}\notag\\ &=I(X\geq t)\frac{\pr\{\dd N^*(t)=1, C\geq t\}}{\pr(T\geq t, C\geq t)} \notag\\ &=I(X\geq t)E\{\dd N^*(t)\mid T\geq t\}\notag\\ &=I(X\geq t)\dd\Lambda(t), \end{align} \]
    • Question: why is the 4th equality true?

Martingale: Properties

  • Interpretation \[\underbrace{\dd M(t)}_{\mbox{residual}} =\underbrace{\dd N(t)}_{\mbox{observed response}} - \underbrace{I(X\geq t)\dd\Lambda(t)}_{\mbox{systematic part}}\]

  • Conditional mean & variance \[ E\{\dd M(t)\mid\mathcal H(t-)\}=0,\,\,\, E\{\dd M(t)^2\mid\mathcal H(t-)\}=I(X\geq t)\dd\Lambda(t) \]

  • Uncorrelated increments (UCI) (for \(t<s\)) \[ E\{\dd M(t)\dd M(s)\}=E\left[\dd M(t)E\{\dd M(s)\mid\mathcal H(s-)\}\right] =0 \]

Martingale Integral

  • Many centered statistic take the form \[ \sum_{i=1}^n\int_0^t h(u)\dd M_i(u) \]
    • Weighted sum of the \(\dd M_i(u)\)

Mean and variance of martingale integral

\[E\left\{\int_0^t h(u)\dd M(u)\right\}=\int_0^t h(u)E\left\{\dd M(u)\right\}=0\]

\[ \begin{align} E\left\{\int_0^t h(u)\dd M(u)\right\}^2 \stackrel{\mbox{UCI}}{=}\int_0^t h(u)^2E\left\{\dd M(u)^2\right\} =\int_0^t h(u)^2\pr(X\geq u)\dd\Lambda(u) \end{align} \]

Martingale Integral: Example

  • Score function \[ \dot l(\theta) = \int_0^\infty h(t;\theta)\dd M(t; \theta) \]
    • Information \[ \mathcal I(\theta) = E\{\dot l(\theta)^2\} = \int_0^\infty h(t;\theta)^2\pr(X\geq t)\dd\Lambda(t;\theta) \]
  • Example: exponential distribution \(h(t;\theta)=\lambda^{-1}\) \[ \mathcal I(\theta) = \int_0^\infty \lambda^{-2}\pr(X\geq t)\lambda\dd t= \lambda^{-1}\int_0^\infty\pr(X\geq t)\dd t \]
    • Compare with standard one by taking negative quadrature of log-likelihood

Conclusion

Notes

  • More parametric families in KP (2002) and KM (2003)
    • (Inverse) Gamma; Log-normal/logistic; Gompertz; Generalized \(F\)
  • Martingale first introduced in survival analysis by O. O. Aalen (1975, 1978)
    • Simplifies derivation of statistical properties
    • Integrand \(h(u)\) can depend on \(\mathcal H(u-)\)
    • Less useful with multivariate outcomes (correlated increments)
      • Current risk depends on past in complex ways

Summary (I)

  • Notation
    • Outcome data: \(T\)
    • Observed data: \(𝑋=π‘‡βˆ§πΆ\) (time), \(𝛿=𝐼(𝑇≀𝐢)\) (status)
    • Counting process: \(𝑁(𝑑)=𝐼(𝑋≀𝑑,𝛿=1)\)
    • Counting process integral \[\delta I(X\leq t) h(X) = \int_0^t h(u)\dd N(u)\]
  • Martingale residual \[\underbrace{\dd M(t)}_{\mbox{residual}} =\underbrace{\dd N(t)}_{\mbox{observed response}} - \underbrace{I(X\geq t)\dd\Lambda(t)}_{\mbox{systematic part}}\]

Summary (II)

  • Martingale integral (e.g., score function) \[ \int_0^t h(u)\dd M(u)=\int_0^t h(u)\left\{\dd N(u)-I(X\geq u)\dd\Lambda(u)\right\} \]

    • Mean zero with easily computable variance