Applied Survival Analysis

Chapter 13 - Composite Endpoints

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Traditional vs hierarchical composites

  2. The restricted mean time in favor (RMT-IF) of treatment

  3. Win ratio: two-sample analysis

  4. Semiparametric regression of win ratio

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\cc}{{\rm c}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\] \[ \newcommand\mymathop[1]{\mathop{\operatorname{#1}}} \] \[ \newcommand{\Ut}{{n \choose 2}^{-1}\sum_{i<j}\sum} \]

$$

$$

Background & Rationale

The Composite Approach

  • Complex outcomes
    • Multivariate/Recurrent events
    • (Semi-)Competing risks
    • Longitudinal measures with survival endpoint
  • Standard methods
    • Joint models (frailty, random effects)
    • Marginal models (component-wise robust methods, cumulative incidence)
  • Traditional composite
    • Time to first event (event-free survival)

Examples and Advantages

  • Examples
    • Cardiovascular: major adverse cardiovascular events (MACE), e.g., death, nonfatal heart failure, myocardial infarction, stroke, etc.
    • Oncology: death and tumor progression (progression-free survival)
  • Advantages
    • More events \(\to\) higher power \(\to\) smaller sample size/lower costs
    • No need for multiplicity adjustment
    • A unified measure of treatment effect
    • Recommended by ICH-E9 “Statistical Principles for Clinical Trials” (1998)

Data and Notation

  • Time-to-event
    • \(D\): survival time; \(N^*_D(t)=I(D\leq t)\)
    • \(N^*_1(t), \ldots, N^*_K(t)\): counting processes for \(K\) nonfatal event types
    • Life history: \(\mathcal H^*(t)=\{N^*_D(u), N^*_1(u), \ldots, N^*_K(u):0\leq u\leq t\}\)
  • Multistate
    • \(Y(t)=0, 1,\ldots, K,\infty\): multistate process; \(\infty=\)death
    • Life history: \(\mathcal H^*(t)= \{Y(u):0\leq u\leq t\}\)
  • Common features
    • Death most important, followed by some other events/states

Traditional Composite Endpoints

  • Time to first event
    • \(N_{\rm TFE}(t) = I\{N^*_D(t)+\sum_{k=1}^KN^*_k(t)\geq 1\}= I\{Y(t)\geq 1\}\)
  • Weighted composite event process
    • \(N_{\rm R}(t)=w_DN^*_D(t)+\sum_{k=1}^Kw_kN^*_k(t)\)
  • Hierarchical composite endpoints (HCE)
    • Death > nonfatal MACE > minor symptoms > …
    • Use more data, avoid arbitrary specification of weights

Motivating Examples

  • Colon cancer trial
    • Levamisole + fluorouracil (\(n=304\)) vs control (\(n=315\))
    • Relapse-free survival
      • 258 (89%) deaths ignored
  • HF-ACTION trial
    • Exercise training (\(n=205\)) vs usual care (\(n=221\))
    • Hospitalization-free survival
      • 82 (88%) deaths + 707 (69%) hospitalizations ignored

Hierarchical Composite Endpoints

  • Restricted mean time in favor (RMT-IF)
    • Nonparametric measure of effect size on HCE
    • Net average time treatment gains in a more favorable state
      • An extension of RMST
    • Uses all events (hierarchically)
  • Win ratio
    • Ratio of probability of better / worse outcomes
    • Initially two-sample comparison (Pocock et al., 2012)
    • Extended to semiparametric regression

Restricted Mean Time in Favor

Outcome Data

  • Target of inference
    • Multistate outcomes \[Y(t) \in \{0, 1,\ldots, K, \infty\}\]
      • \(0\): initial state (e.g., remission)
      • \(1, \ldots, K\): a series of progressively worse states
      • \(\infty\): death
    • Examples
      • \(1\): relapse; \(2\): metastasis
      • \(1, 2, \ldots\): cumulative number of hospitalizations
    • Two-sample comparison
      • \(Y^{(a)}(t)\): a random patient in group \(a\) (\(a=1\): treatment; \(0\): control)

Time on a Win or Loss

  • Pairwise win-loss time
    • \(Y^{(1)}(t)\) vs \(Y^{(0)}(t)\) over \([0, \tau]\);
      • \(\tau\): restiction time (e.g., 5 years)
    • Win time \(=\) time residing in a lower-tiered (thus more favorable) state \[ W^{(a, 1-a)}(\tau)=\int_0^\tau I\{Y^{(a)}(t)<Y^{(1-a)}(t)\}{\rm d}t \]

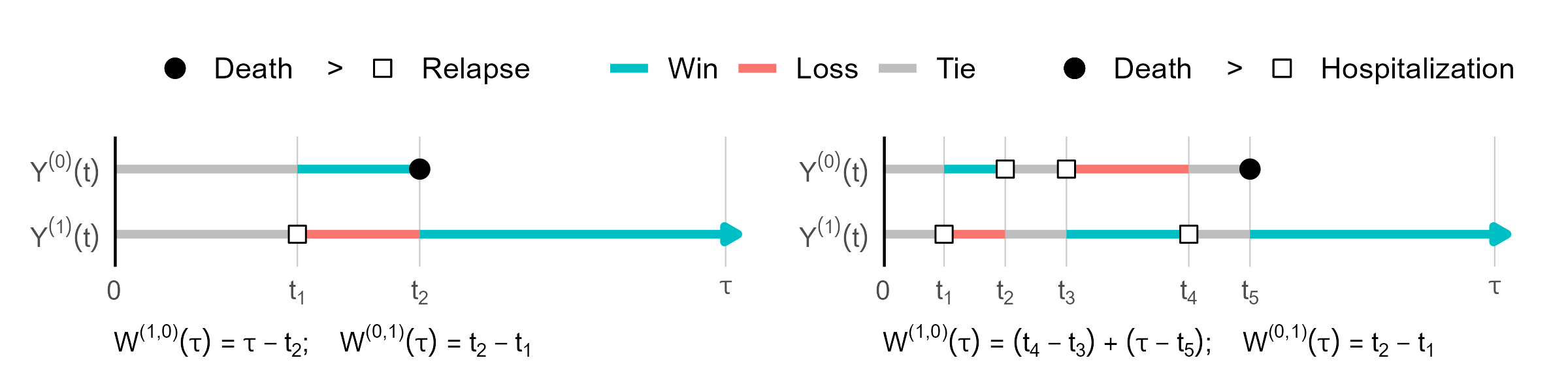
Net Average Win Time

  • Restricted mean time in favor (RMT-IF) of treatment \[ \mu(\tau) = E\{W^{(1, 0)}(\tau)\} - E\{W^{(0, 1)}(\tau)\} \]
    • \(E\{W^{(1, 0)}(\tau)\}\): average win time by treatment vs control
    • \(E\{W^{(0, 1)}(\tau)\}\): average loss time by treatment vs control
    • \(\mu(\tau)\): net average win time by treatment vs control
      • Reduces to difference in RMST in life-death model
    • Decomposition: Time won on which component?
      • Extra survival time + extra relapse-free time + …

Decomposition

  • Stage-wise effects \[\mu(\tau) = \sum_{k=1}^{K,\infty} \mu_k(\tau)\]
    • Time won on \(k\)th state (being in a better state) \[W_k^{(a, 1-a)}(\tau)=\int_0^\tau I\{Y^{(a)}(t)<Y^{(1-a)}(t) = k\}{\rm d}t\]
    • Net average win time on state \(k\) \[ \mu_k(\tau)= E\{W_k^{(1, 0)}(\tau)\} - E\{W_k^{(0, 1)}(\tau)\} \]
      • \(\mu_\infty(\tau)\): net win time on survival \(=\) difference in \(\tau\)-RMST (regardless of other states)
      • \(\mu_2(\tau)\): extra metastasis-free time; \(\mu_1(\tau)\): extra relapse-free time

Simplify for Progressive Processes

  • Progressive process \[Y^{(a)}(t)\leq Y^{(a)}(s) \mbox{ for all } 0\leq t\leq s\]
    • Transition time \(T_k^{(a)}\): time to transition to a state \(\geq k\)
      • \(T_1^{(a)}\): time to relapse/metastasis/death
      • \(T_2^{(a)}\): time to metastasis/death
      • \(T_\infty^{(a)}=D^{(a)}\): time to death
    • Reformulation: \[Y^{(a)}(\cdot)\equiv \big\{0\leq T_1^{(a)}\leq\cdots\leq T_K^{(a)}\leq T_\infty^{(a)}\big\}\]
      • A progressive process \(\Longleftrightarrow\) a sequence of transition marks

Delve into Estimand

  • Average win time on state \(k\)
    • Re-expression with \(S_k^{(a)}(t)=P\{T_k^{(a)}> t\}\) \[\begin{align} E\{W_k^{(a, 1-a)}(\tau)\}&=E\left\{\int_0^\tau I\{Y^{(a)}(t)<Y^{(1-a)}(t) = k\}{\rm d}t\right\}\\ &=\int_0^\tau P\{Y^{(a)}(t)< k\}P\{Y^{(1-a)}(t) = k\}{\rm d}t\\ &=\int_0^\tau P\{T_k^{(a)}> t\}P\{T_k^{(1-a)}\leq t < T_{k+1}^{(1-a)}\}{\rm d}t\\ &=\int_0^\tau S_k^{(a)}(t)\left\{S_{k+1}^{(1-a)}(t) - S_k^{(1-a)}(t)\right\}{\rm d}t\\ \end{align}\]
    • Net average win time \[\mu_k(\tau)=E\{W_k^{(1, 0)}(\tau)\}-E\{W_k^{(0, 1)}(\tau)\}= \int_0^\tau \left\{S_k^{(1)}(t)S_{k+1}^{(0)}(t) - S_k^{(0)}(t)S_{k+1}^{(1)}(t)\right\}{\rm d}t\]

Observed Data & Estimation

  • Censored observations \[ (X_k^{(a)}, \delta_k^{(a)}),\,\,\, k =1,\ldots, K, \infty \]
    • \(X_k^{(a)}= \min(T_k^{(a)}, C^{(a)})\); \(\delta_k^{(a)}= I(T_k^{(a)}\leq C^{(a)})\); \(C^{(a)}=\)censoring time
    • Kaplan–Meier estimator \(\hat S_k^{(a)}(t)\)
  • Estimation: Plug-in KM estimator \[ \hat\mu_k(\tau)= \int_0^\tau \left\{\hat S_k^{(1)}(t)\hat S_{k+1}^{(0)}(t) - \hat S_k^{(0)}(t)\hat S_{k+1}^{(1)}(t)\right\}{\rm d}t \]
    • Robust variance estimator

Hypothesis Testing

  • Test of overall effect \[ H_0: \mu(\tau)= 0 \]
    • \(\chi_1^2\) test based on \(\hat\mu(\tau)=\sum_{k=1}^{K,\infty}\hat\mu_k(\tau)\)
  • Joint test on components \[ H_0: \mu_1(\tau)=\cdots=\mu_K(\tau)=\mu_\infty(\tau) \]
    • \(\chi_{K+1}^2\) test based on \(\hat\mu_1(\tau),\ldots,\hat\mu_K(\tau),\hat\mu_\infty(\tau)\)
      • Or individual components for secondary analyses

Software: rmt::rmtfit() (I)

  • Input data format (long)
    • Standard multistate
      • status = k for entry into state \(k\), K+1 for death, 0 for censoring
    • Recurrent events with death
      • status = 1 for nonfatal event, 2 for death, 0 for censoring
head(hfaction)
#>       patid       time status trt_ab age60
#>  HFACT00001 0.60506502      1      0     1
#>  HFACT00001 1.04859685      0      0     1
#>  HFACT00002 0.06297057      1      0     1
#>  HFACT00002 0.35865845      1      0     1
#>  HFACT00002 0.39698836      1      0     1
#>  HFACT00002 3.83299110      0      0     1
#>  ...

Software: rmt::rmtfit() (II)

  • Basic syntax
library(rmt)
# trt: binary treatment
obj <- rmtfit(id, time, status, trt, 
              type = c("multistate", "recurrent"))
  • Output: a list of class rmtfit
    • obj$t: \(t\); obj$mu: a matrix of \((K+2)\) rows, \(\hat\mu_k(t)\) in \(k\)th row, \(\hat\mu(t)\) in last; obj$var: variances of point estimates in mu
    • summary(obj, tau) for summary results on \(\mu(\tau)\), including the \(\mu_k(\tau)\)
      • Recurrent events: specify Kmax = k to merge \(\mu_{k+}(\tau)\sum_{k'=k}^K=\mu_{k'}(\tau)\)
    • plot(obj) to plot \(\hat\mu(t)\) against \(t\)

Example: HF-ACTION

  • Exercise training vs usual care
Table 1: Descriptive statistics for a high-risk subgroup (n=426) in HF-ACTION trial.
Usual care (N = 221) Exercise training (N = 205)
Age ≤ 60 years 122 (55.2%) 128 (62.4%)
> 60 years 99 (44.8%) 77 (37.6%)
Follow-up (months) 28.6 (18.4, 39.3) 27.6 (19, 40.2)
Death 57 (25.8%) 36 (17.6%)
Hospitalizations 0 51 (23.1%) 60 (29.3%)
1-3 114 (51.6%) 102 (49.8%)
4-10 49 (22.2%) 39 (19%)
>10 7 (3.2%) 4 (2%)

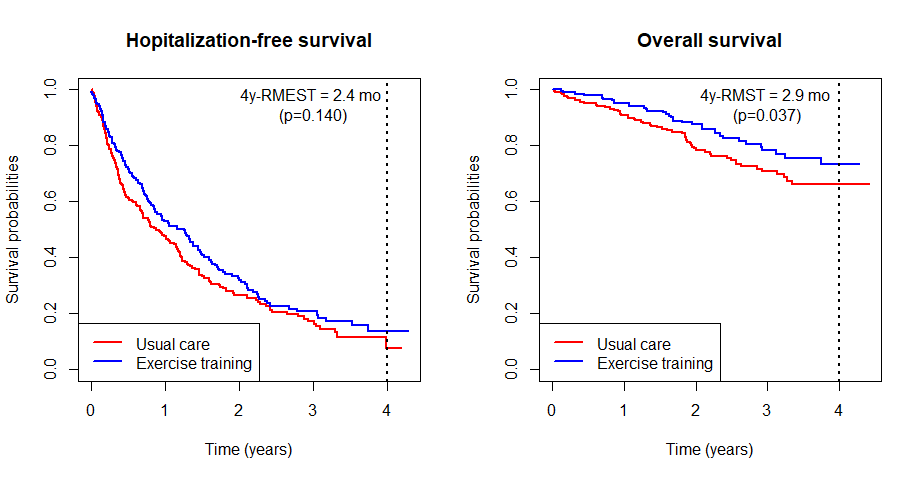
Standard Analyses

  • Traditional composite and overall survival

R-Code

library(rmt)
head(hfaction)
#>       patid       time status trt_ab age60
#>  HFACT00001 0.60506502      1      0     1
#>  HFACT00001 1.04859685      0      0     1
#> ...
# fit RMT-IF
obj <- rmtfit(hfaction$patid, hfaction$time, hfaction$status, hfaction$trt, 
              type = "recurrent")
summary(obj, Kmax=4, tau=3.97) ## combined recurrent events >= 4
# Restricted mean time in favor of group "1" by time tau = 3.97:
#   Estimate    Std.Err Z value Pr(>|z|)    
# Event 1   0.0140515  0.0498836  0.2817 0.778184    
# Event 2   0.0358028  0.0499618  0.7166 0.473619    
# Event 3   0.1385287  0.0409533  3.3826 0.000718 ***
# Event 4+ -0.0064731  0.0600813 -0.1077 0.914203    
# Survival  0.2384169  0.1143484  2.0850 0.037069 *  
# Overall   0.4203268  0.1777363  2.3649 0.018035 *

Graphics

  • \(\hat\mu(t)\) as a function of \(t\)

    • Overall RMT-IF becomes significant after 1 year (see lower CL)
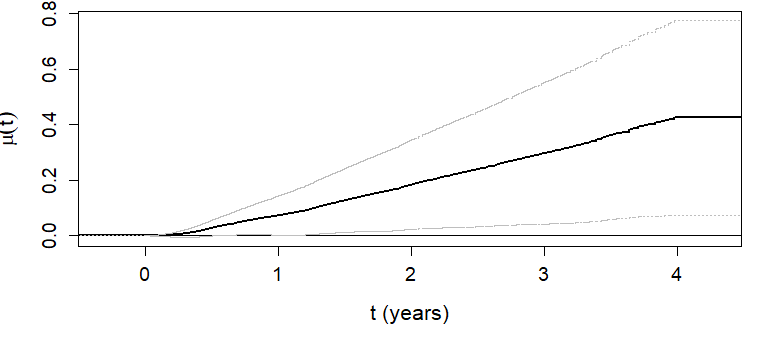
    plot(obj, conf = TRUE, conf.col = "gray", lwd = 2, xlab = "t (years)",
     ylab = "expression(mu(t))", main = "")

Inference Results

  • 4-year RMT-IF of exercise training

    • Training on average gains 5.1 months (\(P\)=0.018) in favorable state

      • 2.9 months net survival \(+\) 2.2 months net time with fewer hospitalizations (little effect on 1st)
Table 2: Analysis of 4-year RMT-IF of exercise training in HF-ACTION trial.
Estimate SE P-value
Hopitalization 2.18 1.22 0.073
1 0.17 0.60 0.778
2 0.43 0.60 0.474
3 1.66 0.49 <0.001
4+ -0.08 0.72 0.914
Death 2.86 1.37 0.037
Overall 5.04 2.13 0.018

Win Ratio Basics

Standard Two-Sample

  • Two-sample comparison (Pocock et al., 2012)
    • Data: \(D_i^{(a)}, T_i^{(a)}, C_i^{(a)}\): survival, hospitalization, censoring times on \(i\)th subject in group \(a\) \((i=1,\ldots, N_a; a= 1, 0)\)
    • Hierarchical composite: Death > hospitalization
    • Pairwise comparisons \[\begin{align} \hat w^{(a, 1-a)}_{ij}&= \underbrace{I(D_j^{(1-a)}< D_i^{(a)}\wedge C_i^{(a)}\wedge C_j^{(1-a)})}_{\mbox{win on survival}}\\ & + \underbrace{I(\min(D_i^{(a)}, D_j^{(1-a)}) > C_i^{(a)}\wedge C_j^{(1-a)}, T_j^{(1-a)}< T_i^{(a)}\wedge C_i^{(1)}\wedge C_j^{(0)})}_{\mbox{inconclusive on survival, win on hospitalization}} \end{align}\]
    • Prioritized comparison on \(\left[0, C_i^{(a)}\wedge C_j^{(1-a)}\right]\)

Pocock’s Rule

  • Win, lose, or tie?

Calculation of Win Ratio

  • Two-sample statistics
    • Win (loss) fraction for group \(a\) (\(1-a\)) \[ \hat w^{(a, 1-a)}=(N_0N_1)^{-1}\sum_{i=1}^{N_a}\sum_{j=1}^{N_{1-a}}\hat w^{(a, 1-a)}_{ij}\]
    • Win ratio statistic \[ WR = \hat w^{(1, 0)} / \hat w^{(0, 1)} \]
    • Other measures
      • Net benefit (proportion in favor): \(\hat w^{(1, 0)} - \hat w^{(0, 1)}\)
      • Win odds: \((\hat w^{(1, 0)} - \hat w^{(0, 1)} + 1)/ (\hat w^{(0, 1)} - \hat w^{(1, 0)} + 1)\)

The Binary Case

  • Consider binary \(Y^{(a)}= 1, 0\)
    • \(\hat w^{(a, 1-a)}_{ij} = I(Y_i^{(a)}> Y_j^{(1-a)})=Y_i^{(a)}(1-Y_j^{(1-a)})\)
    • Win (loss) fraction \[ \hat w^{(a, 1-a)} = (N_1N_0)^{-1}\sum_{i=1}^{N_a}\sum_{j=1}^{N_{1-a}}Y_i^{(a)}(1-Y_j^{(1-a)}) = \hat p^{(a)}(1-\hat p^{(1-a)})\] where \(\hat p^{(a)}= N_a^{-1}\sum_{i=1}^{N_a} Y_i^{(a)}\)
    • Equivalencies \[\begin{align} {\rm Win\,\, ratio}&= \frac{\hat w^{(1, 0)}}{\hat w^{(0, 1)}} = \frac{\hat p^{(1)}(1-\hat p^{(0)})}{\hat p^{(0)}(1-\hat p^{(1)})} = {\rm Odds \,\, ratio}\\ {\rm Net \,\, benefit}&=\hat w^{(1, 0)} - \hat w^{(0, 1)} = \hat p^{(1)}- \hat p^{(0)}= {\rm Risk \,\, difference} \end{align}\]

General Data

  • Outcome data \[\mathcal H^{*{(a)}}(t)=\left\{N^{*{(a)}}_D(u), N^{*{(a)}}_1(u), \ldots, N^{*{(a)}}_K(u):0\leq u\leq t\right\}\]
    • \(N^{*{(a)}}_D(u), N^{*{(a)}}_1(u), \ldots, N^{*{(a)}}_K(u)\): counting processes for death and \(K\) different types of nonfatal events
  • Observed data \[\{\mathcal H^{*{(a)}}(X^{(a)}), X^{(a)}\}\]
    • Life history observed up to \(X^{(a)}= D^{(a)}\wedge C^{(a)}\)

General Rule

  • Win function \[\mathcal W(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(t) =I\left\{\mathcal H^{*{(a)}}(t) \mbox{ is more favorable than } \mathcal H^{*{(1-a)}}(t)\right\}\]
    • Basic requirements
      • (W1) \(\mathcal W(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(t)\) is a function only of \(\mathcal H^{*{(a)}}(t)\) and \(\mathcal H^{*{(1-a)}}(t)\)
      • (W2) \(\mathcal W(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(t)+\mathcal W(\mathcal H^{*{(1-a)}}, \mathcal H^{*{(a)}})(t) \in \{0, 1\}\)
      • (W3) \(\mathcal W(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(t)=\mathcal W(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(D^{(a)}\wedge D^{(1-a)}\wedge t)\)
    • Interpretations
      • (W1) Consistency of time frame
      • (W2) Either win, loss, or tie
      • (W3) No change of win-loss status after death (satisfied if death is prioritized)

Generalized Win Ratio

  • General WR statistics \[\begin{equation}\label{eq:wr:gen_WR} \hat{\mathcal E}_n(\mathcal W)=\frac{(N_1N_0)^{-1}\sum_{i=1}^{N_1}\sum_{j=1}^{N_0}\mathcal W(\mathcal H^{*{(1)}}_{i}, \mathcal H^{*{(0)}}_{j})(X^{{(1)}}_{i}\wedge X^{{(0)}}_{j})} {(N_1N_0)^{-1}\sum_{i=1}^{N_1}\sum_{j=1}^{N_0}\mathcal W(\mathcal H^{*{(0)}}_{j}, \mathcal H^{*{(1)}}_{i})(X^{{(1)}}_{i}\wedge X^{{(0)}}_{j})} \end{equation}\]
    • Window of comparison: \([0, X^{{(1)}}_{i}\wedge X^{{(0)}}_{j}]\), by a general \(\mathcal W\)
    • Stratified win ratio \[ \frac{\text{Weighted sum of within-stratum wins}}{\text{Weighted sum of within-stratum losses}} \]

Pocock’s Win Ratio

  • Win function
    • \(K\) nonfatal events hierarchically ranked
    • \(T^{(a)}_k\): time of first event in \(N_k^{*{(a)}}(t)\) \((k=1,\ldots, K)\) \[\begin{align}\label{eq:wr:PWR} \mathcal W_{\rm P}(\mathcal H^{*{(a)}}, \mathcal H^{*{(1-a)}})(t)&=I\{D^{(1-a)}<D^{(a)}\wedge t\}\notag\\ &\hspace{2mm}+I\{D^{(a)}\wedge D^{(1-a)}>t, T_{1}^{(1-a)}<T_{1}^{(a)}\wedge t\}\notag\\ &\hspace{2mm}+\sum_{k=2}^KI\{\tilde T_{k-1}^{(a)}\wedge \tilde T_{k-1}^{(1-a)}>t, T_{k}^{(1-a)}<T_{k}^{(a)}\wedge t\} \end{align}\]
      • \(\tilde T_{k-1}^{(a)}=D^{(a)}\wedge T_{1}^{(a)}\wedge\cdots\wedge T_{k-1}^{(a)}\)
  • Win ratio statistic: \(\hat{\mathcal E}_n(\mathcal W_{\rm P})\)

Taking Recurrent Events

  • Recurrent-event win ratio (RWR)
    • Death > number of recurrent events > time to last event

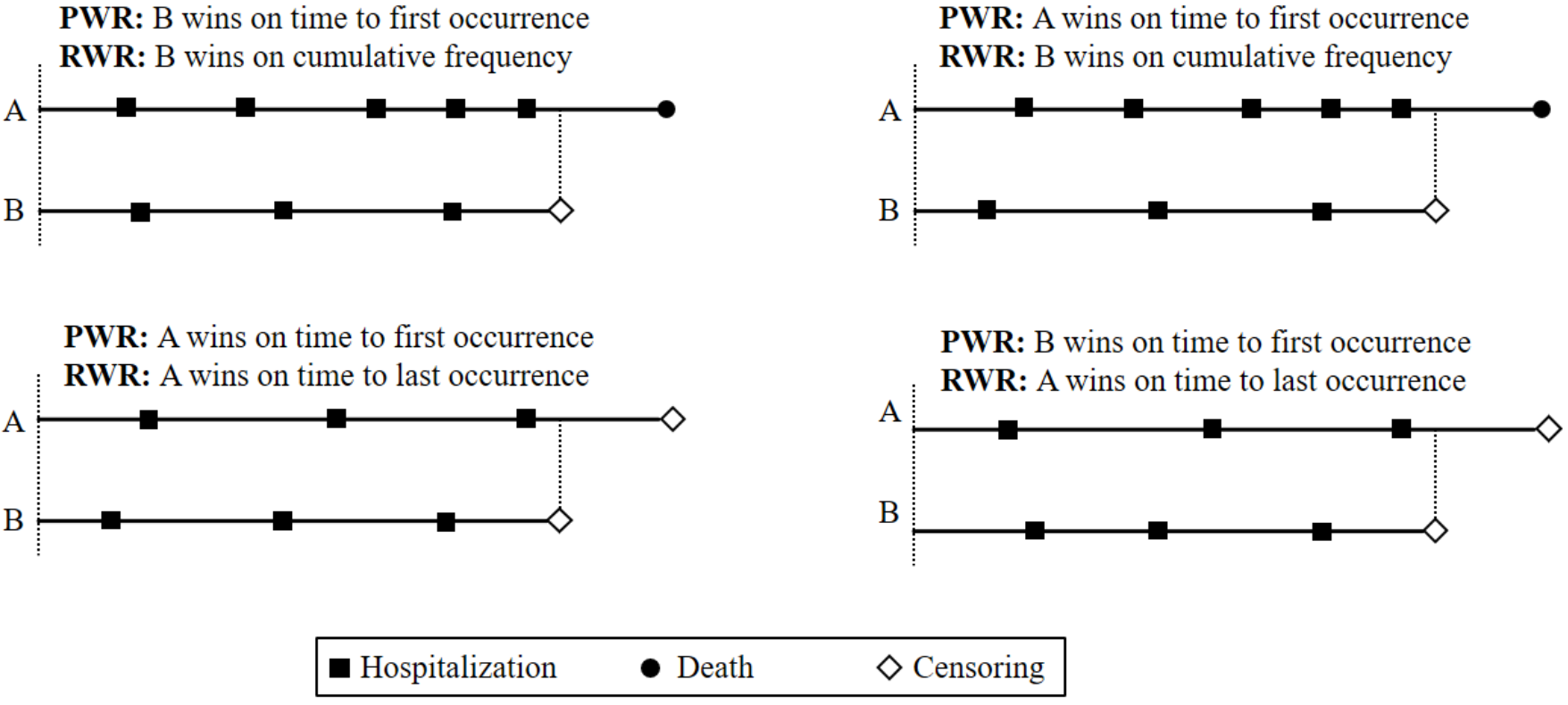
Time-to-First-Event

  • Compare on order of first event
    • Win function \[ \mathcal W_{\rm TFE}(\mathcal H^{*{(a)}},\mathcal H^{*{(1-a)}})(t)=I(\tilde T^{(1-a)}<\tilde T^{(a)}\wedge t) \]
      • \(\tilde T^{(a)}=\min(D^{(a)}, T_1^{(a)},\ldots, T_K^{(a)})\)
    • Allowable but not desirable

Semiparametric Regression of Win Ratio

Regression Framework

  • Motivation
    • Meaningful estimand of effect size
    • Multiple (quantitative) predictors
  • Modelin target
    • Two independent subjects \((\mathcal H_i, Z_i)\) and \((\mathcal H_j, Z_j)\)
      • \(E\{\mathcal W(\mathcal H_i,\mathcal H_j)(t)\mid Z_i, Z_j\}\): Conditional win fraction (probability) for \(i\) against \(j\) at \(t\)
      • \(E\{\mathcal W(\mathcal H_j,\mathcal H_i)(t)\mid Z_i, Z_j\}\): Conditional win fraction (probability) for \(j\) against \(i\) at \(t\)
    • Covariate-specific win ratio \[\begin{equation}\label{eq:cov_spec_curtail_wr} WR(t; Z_i, Z_j;\mathcal W):= \frac{E\{\mathcal W(\mathcal H_i,\mathcal H_j)(t)\mid Z_i,Z_j\}}{E\{\mathcal W(\mathcal H_j,\mathcal H_i)(t)\mid Z_i, Z_j\}} \end{equation}\]
    • Model it against \(Z_i\) and \(Z_j\) to study covariate effect on WR

Model Specification

  • Proportional win-fractions (PW) model \[\begin{equation}\label{eq:wr_reg} WR(t\mid Z_i, Z_j;\mathcal W)=\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\} \end{equation}\]
    • PW: covariate-specific win/loss fractions proportional over time
      • WR constant over time
    • \(\beta\): log-win ratio associated with unit increases in covariates (regardless of follow-up time)
    • Semiparametric model
      • Parametric covariate-specific WRs
      • Nonparametric in other aspects (baseline event rates, etc.)
    • Denote model by PW\((\mathcal W)\)
      • Stresses model’s dependency on \(\mathcal W\) chosen

Special Cases

  • Pocock’s two-sample WR
    • \(Z = 1, 0\)
    • \(\exp(\beta)\): WR comparing group \(z=1\) with group \(0\)
  • Cox PH model
    • PW\((\mathcal W_{\rm TFE})\) \(\Leftrightarrow\) Cox PH model on time to first event

Estimation

  • Construction of estimating function
    • Observed win process \(\delta_{ij}(t)=\mathcal W(\mathcal H_i,\mathcal H_j)(X_i\wedge X_j\wedge t)\)
    • Determinancy (win or loss): \(R_{ij}(t)=\delta_{ij}(t)+\delta_{ji}(t)\)
    • Mean-zero residual \[\begin{equation}\label{eq:wr:resid} M_{ij}(t\mid Z_i, Z_j;\beta)=\underbrace{\delta_{ij}(t)}_{\rm observed\,\,win} - \underbrace{R_{ij}(t)\frac{\exp\left\{\beta^{\rm T}\left( Z_i- Z_j\right)\right\}}{ 1+\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\}}}_{\rm model-based\,\, prediction} \end{equation}\]
    • Estimating equation \[\begin{equation}\label{eq:wr:ee} \Ut\int_0^\infty (Z_i - Z_j) h(t; Z_i, Z_j)\dd M_{ij}(t \mid Z_i, Z_j;\beta)=0 \end{equation}\]
      • Weight function \(h(t; Z_i, Z_j)\equiv 1\)

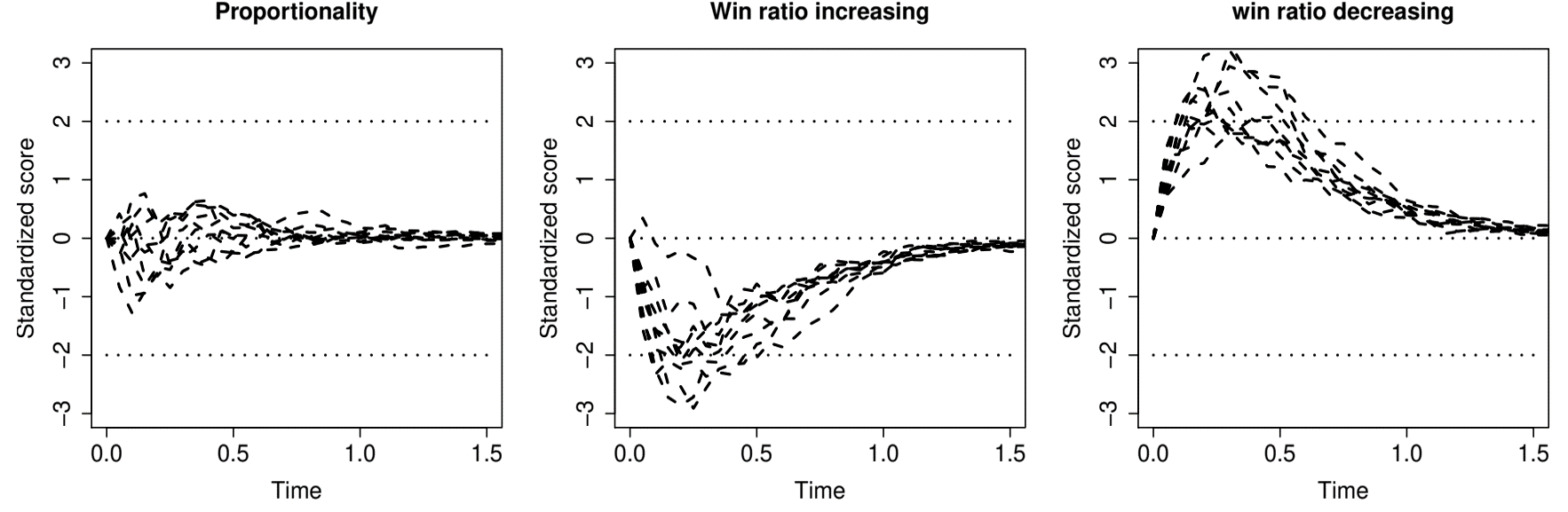
Checking Proportionality

  • Cumulative residuals
    • Rescaled \(\hat U_n(t)=\Ut(Z_i - Z_j)\underbrace{M_{ij}(t \mid Z_i, Z_j;\hat\beta)}_{\rm observed\,\, minus\,\, model-based\,\,wins\,\, by\,\, t}\)

Software: WR::pwreg() (I)

  • Input data format
    • status = 1 for death, 2 for nonfatal events, 0 for censoring
library(WR)
#> Loading required package: survival
head(non_ischemic)
#>   ID time status trt_ab age sex Black.vs.White Other.vs.White   bmi
#> 1  1  221      2      0  62   1              0              0 25.18
#> 2  1  383      0      0  62   1              0              0 25.18
#> 3  2   23      2      0  75   1              1              0 22.96
#> 4  2 1400      0      0  75   1              1              0 22.96
#> ...

Software: WR::pwreg() (II)

  • Basic syntax for PW\((\mathcal W_{\rm P})\)
    • ID: subject identifier
    • Z: covariate matrix; strata: possible stratifier (categorical)
# fit PW model (death > nonfatal event)
obj <- pwreg(ID, time, status, Z, strata = NULL)
  • Output: an object of class pwreg
    • obj$beta: \(\hat\beta\)
    • obj$Var: \(\hat\var(\hat\beta)\)
    • print(obj) to summarize regression results

Software: WR::score.proc()

  • Checking proportionality
    • obj: a pwreg object
# fit PW model (death > nonfatal event)
score.obj <- score.proc(obj)
  • Output: an object of class score.proc
    • score.obj$t: \(t\)
    • score.obj$score: a matrix with rescaled residual process for each covariate per row
    • plot(score.obj, k): plot the rescaled residuals for \(k\)th covariate

HF-ACTION: Data

  • Another subset of HF-ACTION
    • Population: \(n=451\) non-ischemic patients followed over median length of 31.6 months
    • Endpoints: death > first hospitalization
    • Predictors: training vs usual care, age, sex, race, bmi, LVEF, medications, etc.
library(WR)
#> Loading required package: survival
head(non_ischemic)
#>   ID time status trt_ab age sex Black.vs.White Other.vs.White   bmi  ...
#> 1  1  221      2      0  62   1              0              0 25.18
#> 2  1  383      0      0  62   1              0              0 25.18
#> 3  2   23      2      0  75   1              1              0 22.96
#> 4  2 1400      0      0  75   1              1              0 22.96
#> ...

HF-ACTION: Regression Coding

  • Set up PW\((\mathcal W_{\rm P})\)
# extract variables and covariate matrix
ID <- non_ischemic[,"ID"]
time <- non_ischemic[,"time"]
status <- non_ischemic[,"status"]
Z <- as.matrix(non_ischemic[, 4:(3+p)], nr, p)
# pass the parameters into the function
pwreg.obj <- pwreg(ID, time, status, Z)
# print out results
print(pwreg.obj)

HF-ACTION: Regression Results

  • Summary results
    • Training \(\exp(0.191) - 1= 21\%\) more likely to get favorable outcome than UC
    • Race differences substantial and significant
    • LVEF: 1% increases win likelihood by \(\exp(0.021) = 1.02\) (\(p\)-value 0.013)
#> Estimates for Regression parameters:
#>                     Estimate         se z.value p.value
#> Training vs Usual  0.1906687  0.1264658  1.5077 0.13164
#> Age (year)        -0.0128306  0.0057285 -2.2398 0.02510 *
#> Male vs Female    -0.1552923  0.1294198 -1.1999 0.23017
#> Black vs White    -0.3026335  0.1461330 -2.0709 0.03836 *
#> Other vs White    -0.3565390  0.3424360 -1.0412 0.29779
#> BMI               -0.0181310  0.0097582 -1.8580 0.06316 .
#> LVEF               0.0214905  0.0086449  2.4859 0.01292 *
#> ...

HF-ACTION: Residual Analyses

  • Checking proportionality
score.obj <- score.proc(pwreg.obj)
par(mfrow = c(1, 3)) # plot residual processes for treatment, age, LVEF
for(i in c(1, 2, 7)){
  plot(score.obj, k = i, xlab = "Time (Days)")
}

Conclusion

Notes

  • Before win ratio
    • Continuous outcome: Wilcoxon (1945), Mann & Whitney (1947)
    • Hierarchical endpoints: Finkelstein and Schoenfeld (1999), Buyse (2010)
  • More on RMT-IF
  • Hierarchical endpoints
    • Gaining popularity and an active area of research

Summary

  • RMT-IF
    • Model-free, component-wise decomposable \[ \mu(\tau) = \underbrace{E\{W^{(1, 0)}(\tau)\}}_{\rm win\,time\,by\,\tau} - \underbrace{E\{W^{(0, 1)}(\tau)\}}_{\rm loss\,time\,by\,\tau} \]
    • rmt::rmtfit()
  • Win ratio regression
    • Proportionality and multiplicativity \[ WR(t\mid Z_i, Z_j;\mathcal W)=\exp\left\{\beta^{\rm T}\left(Z_i- Z_j\right)\right\} \]
    • \(\exp(\beta)\): WRs with unit increases in covariates
    • WR::pwreg()