Applied Survival Analysis

Chapter 11 - Joint Analysis of Longitudinal and Survival Data

Lu Mao
lmao@biostat.wisc.edu

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Linear mixed effects models for longitudinal data
  2. A two-stage joint modeling approach
  3. Extensions and dynamic prediction
  4. Analysis of an anti-retroviral drug trial
  5. An example with multiple biomarkers*

\[\newcommand{\d}{{\rm d}}\] \[\newcommand{\T}{{\rm T}}\] \[\newcommand{\dd}{{\rm d}}\] \[\newcommand{\cc}{{\rm c}}\] \[\newcommand{\pr}{{\rm pr}}\] \[\newcommand{\var}{{\rm var}}\] \[\newcommand{\se}{{\rm se}}\] \[\newcommand{\indep}{\perp \!\!\! \perp}\] \[\newcommand{\Pn}{n^{-1}\sum_{i=1}^n}\]

Overview

  • Background
    • Biomarkers, quality of life measured longitudinally while being followed for a clinical event
  • Joint modeling
    • Association between biomarker and (clinical) endpoint
      • CD4 cell count \(\to\) death from AIDS
      • Serum creatinine/eGFR \(\to\) kidney failure
    • Dependent dropout (death) in longitudinal analysis
    • Dynamic prediction of survival/biomarker

Linear Mixed Effects Models

Longitudinal Data

  • Outcome Data
    • \(Y_{i1},\ldots, Y_{in_i}\) longitudinal responses measured on subject \(i\) at the \(t_{ij}\)
    • \(t_{i1},\ldots, t_{in_i}\): measurement occasions for subject \(i\)
    • \(Z_{ij}\): covariates on subject \(i\) at \(t_{ij}\)
      • Patient characteristics \(+\) time trend (functions of \(t_{ij}\))
  • Longitudinal regression
    • Mean model: \(E(Y_{ij}\mid Z_{ij}) = \gamma_0 + \gamma^\T Z_{ij}\)
    • Example: \(E(Y_{ij}\mid A_i)=\gamma_0+\gamma_1A_i+\gamma_2t_{ij}+\gamma_3A_it_{ij}\)
      • \(Z_{ij}=(A_i, t_{ij}, A_it_{ij})^\T\); \(A_i = 1, 0\): treatment indicator

Handling Correlations

  • Challenge: correlation of the \(Y_{ij}\) over \(t_{ij}\)
    • Standard least squares invalid or suboptimal
  • Linear mixed effects (LME) models \[\begin{equation}\label{eq:longit:lme} Y_{ij}=\gamma_0+\gamma^\T Z_{ij}+b_i^\T\tilde Z_{ij}+\epsilon_{ij} \end{equation}\]
    • \(\tilde Z_{ij}\) contains 1 and a subset of \(Z_{ij}\)
    • \(b_i\sim \mathcal N(0,\Sigma_b)\): subject-specific random effects (intercept, slope)
      • Induces correlation within subject
    • \(\epsilon_{ij}\sim_{\rm i.i.d.} \mathcal N(0,\sigma^2)\): random measurement error
    • True values: \(E(Y_{ij}\mid Z_{ij}, b_i)=\gamma_0+\gamma^\T Z_{ij}+b_i^\T\tilde Z_{ij}\)

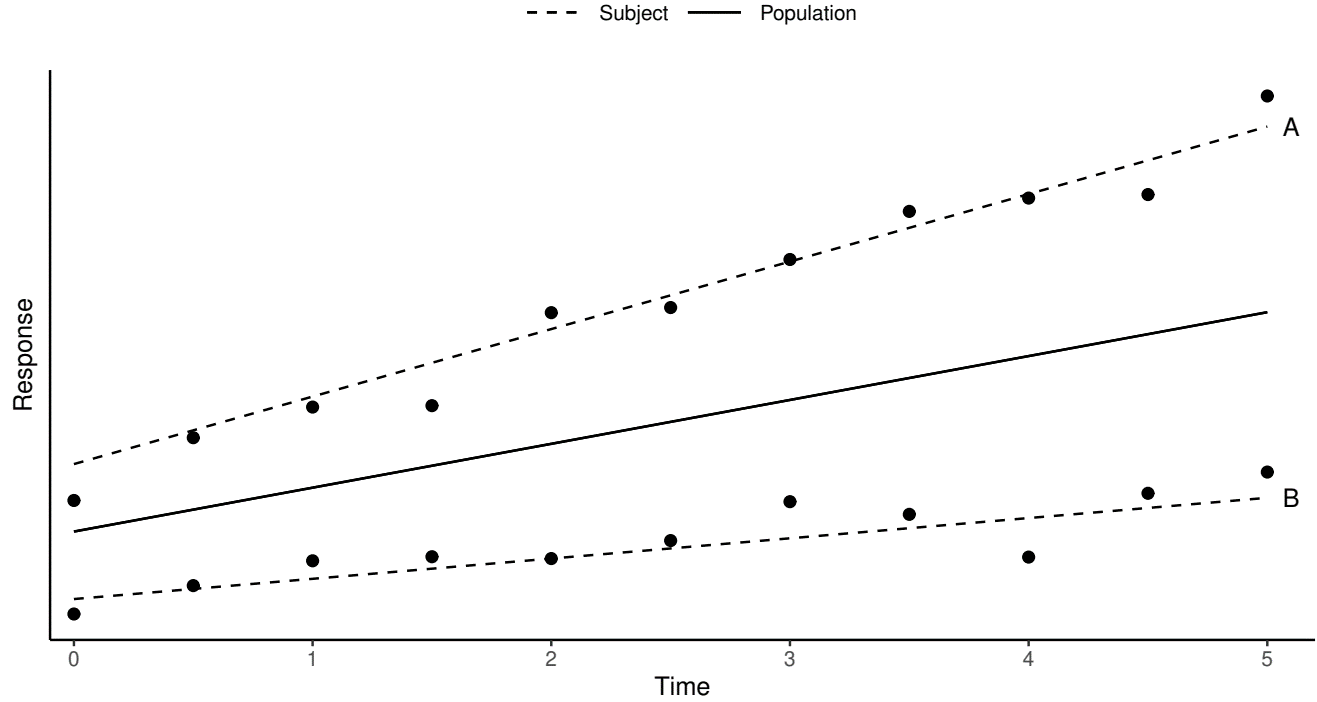
LME Example

  • Random intercept \(+\) random slope
    • \(Y_{ij}=\gamma_0+\gamma_1t_{ij}+b_{i0}+b_{i1}t_{ij}+\epsilon_{ij}\)
      • \(Z_{ij}=t_{ij}\), \(\tilde Z_{ij}=(1, t_{ij})^\T\), \(b_i=(b_{i0},b_{i1})^\T\)

Estimation and Inference

  • EM algorithm with \(b_i\) as missing data
    • \(E\)-step: conditional expectation of \(b_i\) and \(b_i^2\) given observed data
      • Explicit under multivariate normal
    • \(M\)-step: (weighted) least squares
  • Variance components
    • \(\hat\Sigma_b\): between-subject
    • \(\hat\sigma_2\): within-subject

Two-Stage Joint Modeling

Rationale

  • Traditional Cox model
    • Survival vs observed biomarker as (internal) time-varying covariates
  • Limitations
    • Biomarker measured at discrete times, with missing data in-between
    • Biomarker measured with error (sometimes with erratic noise)
  • Two-stage modeling
    • Longitudinal sub-model: true biomarker process over continuous time
    • Survival sub-model: Cox model with true biomarker process as time-varying covariate

Longitudinal Sub-Model

  • Conceptual setup
    • \(Y_i(t)\): latent biomarker process at time \(t\)
      • \(Y_i(t_{ij}) = Y_{ij}\)
    • \(Z_i(t), \tilde Z_i(t)\): latent covariate processes at time \(t\)
      • \(Z_i(t_{ij}) = Z_{ij}\); \(\tilde Z_i(t_{ij}) = \tilde Z_{ij}\)
  • Reformulation of LME \[\begin{equation}\label{eq:longit:longit_sub} Y_i(t)=m_i(t)+\epsilon_i(t), \end{equation}\]
    • \(m_i(t)=\gamma_0+\gamma^\T Z_i(t)+b_i^\T\tilde Z_i(t)\): True biomarker process
    • \(\epsilon_i(t)\): Error process

Survival Sub-Model

  • Model specification \[\begin{equation}\label{eq:longit:survival_sub} \pr\{t\leq T_i<t+\dd t\mid Z_i^*, \overline m_i(t)\}=\exp\{\beta^\T Z_i^*+\nu m_i(t)\}\lambda_0(t)\dd t \end{equation}\]
    • \(T_i\): survival endpoint
    • \(\overline m_i(t)=\{m_i(u):0\leq u\leq t\}\): biomarker history
    • \(Z_i^*\): baseline covariates to be adjusted for in survival model
    • \(\nu\): log-hazard ratio with one unit increase in current biomarker
  • Estimation
    • \(E\)-step: conditional expectation of the \(b_i\) (numerical integration)
    • \(M\)-step: (weighted) least squares \(+\) partial-likelihood score

Extensions and Dynamic Prediction

Interaction and Trend Effect

  • Biomarker effect by baseline group
    • Biomarker \(\times\) baseline interaction \[ \pr(t\leq T_i<t+\dd t\mid Z_i^*, \overline m_i(t))=\exp\big\{\beta^\T Z_i^*+\nu m_i(t)+ \tilde\nu^\T Z_i^*m_i(t)\big\}\lambda_0(t)\dd t \]
  • Effect of biomarker trend (change rate)
    • Longitudinal sub-model \[\begin{equation}\label{eq:longit:longit_sub_slope} m_i(t)=\gamma_0+\gamma^\T Z_i+\eta t+b_{i0}+b_{i1}t, \end{equation}\]
    • Survival sub-model \[\begin{equation}\label{eq:longit:survival_sub_rand} \pr(t\leq T_i<t+\dd t\mid Z_i, b_i)=\exp\{\beta^\T Z_i+\nu_0b_{i0}+\nu_1b_{i1}\}\lambda_0(t)\dd t. \end{equation}\]
    • \(\nu_1\):log-hazard ratio by unit increase in biomarker change rate

GLMM

  • Generalized linear mixed-effects models (GLMM)

    • Binary, categorical, count biomarkers \[\begin{equation}\label{eq:longit:glmm} g\left[E\{Y_i(t)\mid Z_i,b_i\}\right]=\gamma_0+\gamma^\T Z_i(t)+b_i^\T\tilde Z_i(t) \end{equation}\]

      • Example : logistic regression with \(g(x)=\log\{x/(1-x)\}\)

    • Subject-level trajectory \[m_i(t)=g^{-1}\left\{\gamma_0+\gamma^\T Z_i(t)+b_i^\T\tilde Z_i(t)\right\}\]

    • Survival sub-model: plug in \(m_i(t)\) or \(g\{m_i(t)\}\)

Multivariate Models

  • Multple biomarkers
    • Longitudinal sub-models \[ m_{ik}(t)=\gamma_{0k}+\gamma_k^\T Z_i(t)+b_{ik}^\T\tilde Z_i(t), \quad k =1,\ldots, K \]
    • Survival sub-model \[ \pr\{t\leq T_i<t+\dd t\mid Z_i^*, \overline m_{i1}(t), \ldots, \overline m_{iK}(t)\}=\exp\left\{\beta^\T Z_i^*+\sum_k\nu_k m_{ik}(t)\right\}\lambda_0(t)\dd t \]
  • Multple events
    • Shared-fraity sub-models \[\begin{equation}\label{eq:longit:survival_sub_mult} \pr\{t\leq T_{ik}<t+\dd t\mid \xi_i, Z_i^*, \overline m_i(t)\}=\xi_i\exp\{\beta_k^\T Z_i^*+\nu_k m_i(t)\}\lambda_{0k}(t)\dd t \end{equation}\]

Dynamic Prediction

  • Setup
    • Question: Prediction of survival/biomarker given current data
    • Observed biomarker history: \(\overline Y_i(u)=\{Y_i(t_{ij}):0\leq t_{ij}\leq u\}\)
  • Prediction of future outcomes
    • Survival \[ \mathcal S_i\{t\mid u, \overline Y_i(u)\}=\pr\{T_i > t \mid T_i>u, \overline Y_i(u)\} \]
    • Biomarker \[ \mathcal M_i(t\mid u)=E[Y_i(t)\mid T_i>u, \overline Y_i(u)] \]
    • Both computable under fitted model

Software: JM package (I)

  • Longitudinal sub-model
    • id: subject identifier; y: response; covariates: \(Z\); cov_rand: \(\tilde Z\)
# Longitudinal sub-model
longit_sub <- lme(y ~ covariates, 
                  random = ~ cov_rand | id, data = df)
  • Survival sub-model
    • covariates1: \(Z^*\); x = TRUE to include \(Z^*\) in model fit
df_surv <- df[!duplicated(df$id), ] # De-duplicate data
# Fit Cox model without biomarker 
surv_sub <- coxph(Surv(time, status) ~ covariates1, 
                  data = df_surv, x = TRUE)

Software: JM package (II)

  • Joining two sub-models
    • "occasion": time variable in longitudinal model (same unit as time)
    • "piecewise-PH-aGH": piecewise linear baseline with 6 internal knots
# combine the two models
obj <- jointModel(longit_sub, surv_sub, timeVar = "occasion",
                            method = "piecewise-PH-aGH")
  • Output: a list of class jointModel
    • obj$coefficients: main component
      • betas: \(\hat\gamma\); gammas: \(\hat\beta\); alpha: \(\hat\nu\); sigma: \(\hat\sigma\); D: \(\hat\Sigma_b\)
    • Summary(obj) to print summary results

Software: JMbayes2 package (I)

  • Multiple non-Gaussian biomarkers (Bayesian approach)
    • mixed_model(formula, family = binomial()): logistic GLMM
# Fit longitudinal sub-models (linear time)
# Biomarker 1 (Continuous)
longit_sub1 <- lme(y1 ~ covariates + obstime, 
                   random = ~ obstime | id, data = df)
# Biomarker 2 (Binary)
longit_sub2 <- mixed_model(y2 ~ covariates + obstime, 
                           random = ~ obstime | id, data = df,
                           family = binomial())

# Fit the Cox sub-model without the biomarker
surv_sub <- coxph(Surv(time, status) ~ covariates, 
                  data = df_surv, x = TRUE)

Software: JMbayes2 package (II)

  • Join models (Bayesian approach)
    • Specify functional_forms for each biomarker
      • value(): \(m_{ik}(t)\) (\(g\{m_{ik}(t)\}\) for GLMM)
      • slope(): \(\d m_{ik}(t)/\d t\);\(\quad\) area(): \(\int_0^t m_{ik}(u)\d u\)
# Define functional forms of biomarkers to include in joint model
fForms <- list("y1" = ~ value(y1) + slope(y1), 
               "y2" = ~ value(y2) + slope(y2))
# Combine the longitudinal and survival sub-models
obj <- jm(surv_sub, list(longit_sub1, longit_sub2), 
          time_var = "obstime",
          functional_forms = fForms)
# Dynamic prediction
pred <- predict(obj, newdata = df_new)

Anti-Retroviral Drug Trial

Study Background

  • Study information
    • Population: 467 HIV-positive patients randomized to receive didanosine (ddI) and zalcitabine (ddC) followed over a median length of 13.2 month
    • Primary endpoint : All-cause mortality
    • Longitudinal biomarker: number of CD4 cells per cubic millimeter of blood (square-root transformed), measured at baseline, 2, 6, 12, 18 months
    • Aims: evaluate associations between
      • Treatment (ddI vs ddC) \(\to\) CD4 cell count
      • CD4 cell count \(\to\) mortality

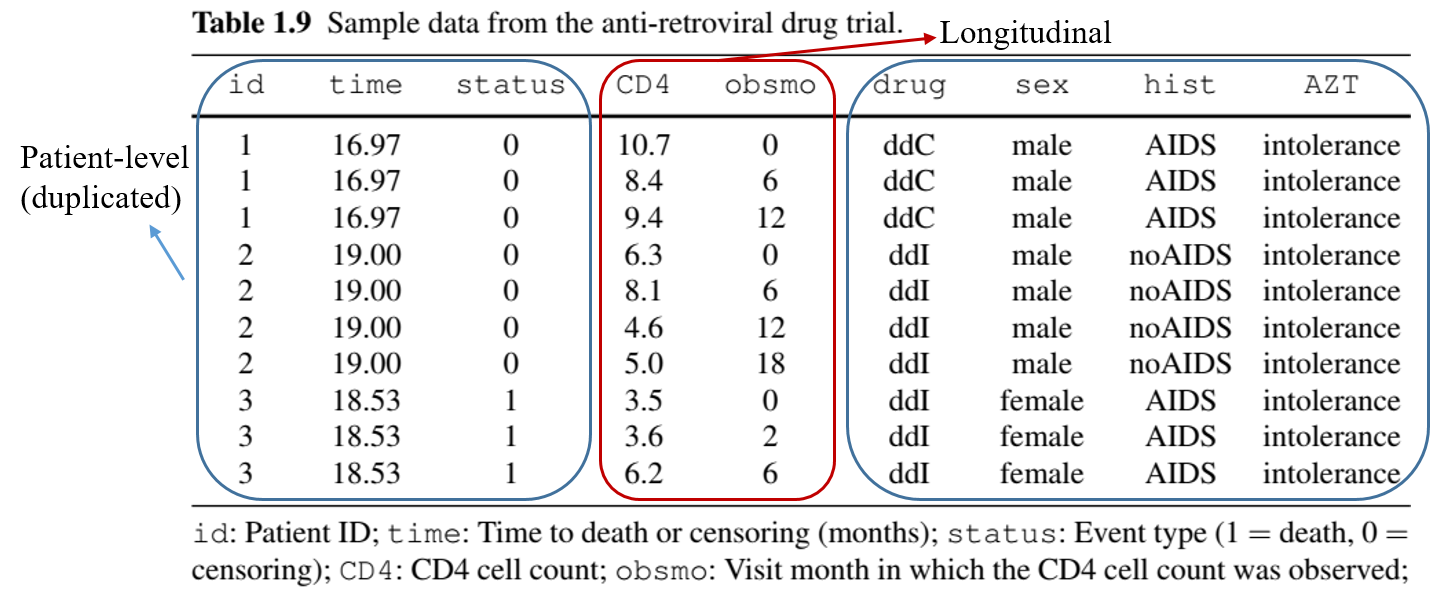
Study Data

  • Data format
    • Repeated measures of CD4 cell count + death

Joint Modeling of Mortality and CD4

  • LME + Cox model
    • Random intercept & time slope
    • Fixed effects: time, treatment \(\times\) time
      • adjusting for patient sex, history of HIV infection
# Longitudinal sub-model: linear time
longit_sub <- lme(CD4 ~ obsmo + obsmo:drug + sex + hist,
                  random = ~ obsmo|id, data = df)
# Survival sub-model
df_surv <- df[!duplicated(df$id),]
surv_sub <- coxph(Surv(time, status) ~ drug + sex + hist,
                  data = df_surv, x = TRUE)

Summary Results (I)

  • Longitudinal sub-model
# Combine the two models
obj_joint <- jointModel(longit_sub, surv_sub, timeVar = "obsmo",
                            method = "piecewise-PH-aGH")
summary(obj_joint)
#> Variance Components:
#>              StdDev    Corr
#> (Intercept)  3.9797  (Intr)
#> obsmo        0.1928 -0.0890
#> Residual     2.0428    
#> Longitudinal Process
#>                 Value Std.Err z-value p-value
#> (Intercept)    5.8614  0.6562  8.9322 <0.0001
#> obsmo         -0.1922  0.0240 -8.0175 <0.0001
#> sexmale       -0.3823  0.6642 -0.5757  0.5649
#> histnoAIDS     4.8617  0.4091 11.8835 <0.0001
#> obsmo:drugddI  0.0219  0.0333  0.6558  0.5120

Summary Results (II)

  • Survival sub-model
summary(obj_joint)
#> Event Process
#>              Value Std.Err z-value p-value
#> drugddI     0.3487  0.1576  2.2118  0.0270
#> sexmale    -0.3313  0.2608 -1.2701  0.2040
#> histnoAIDS -0.5873  0.2255 -2.6040  0.0092
#> Assoct     -0.2569  0.0374 -6.8708 <0.0001 # CD4 effect
#> ...
  • Results
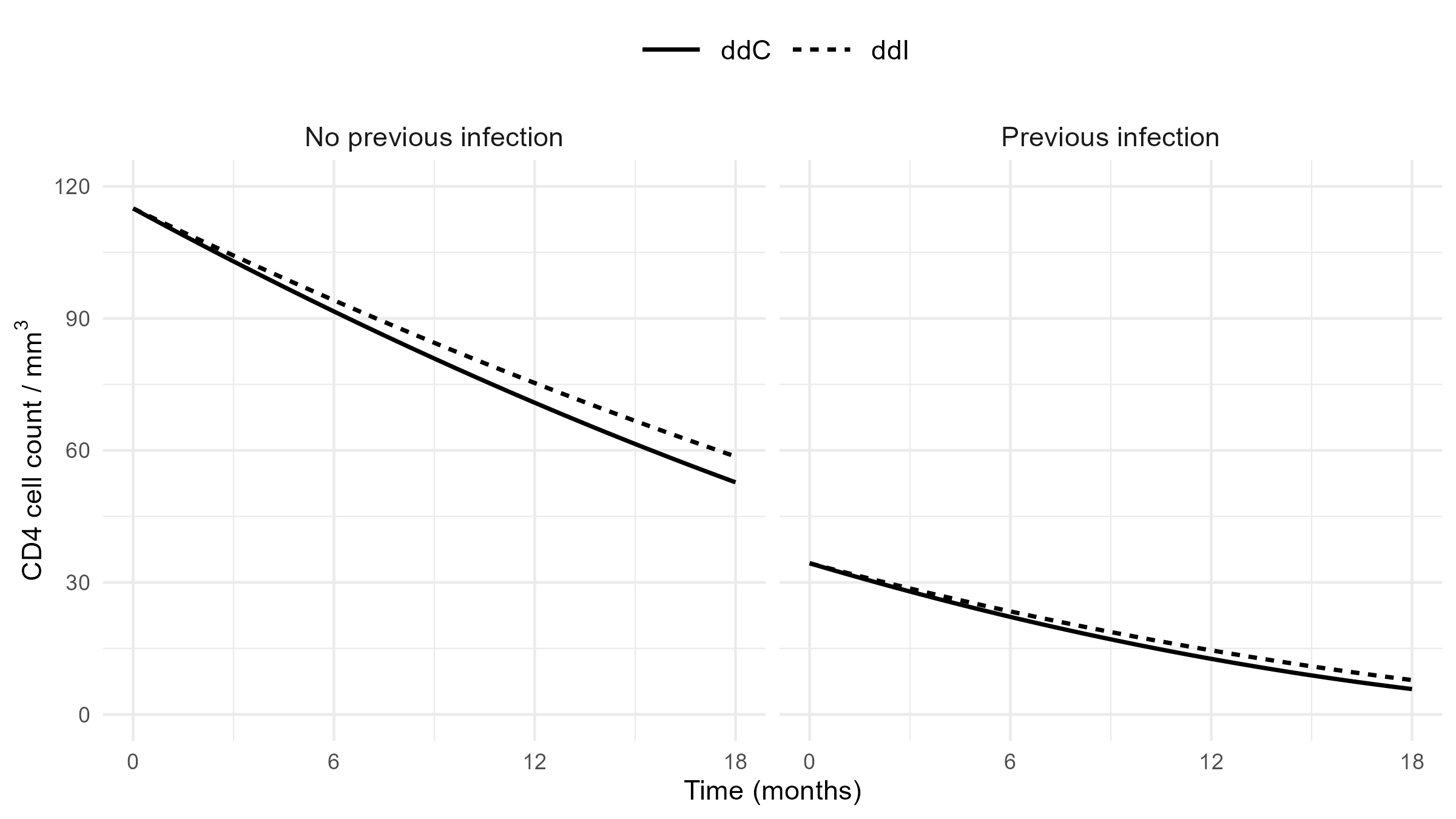
    • ddI leads to slightly slower rate of decline (by 0.0219 per month) in \(\sqrt{\rm CD4}\)
    • One unit decline in \(\sqrt{\rm CD4}\) increases the risk of death by \(\exp(0.2569) = 1.30\)-fold (p-value \(< 0.0001\))

Mean CD4 Trajectory

  • Model-based predictions

Multiple Biomarkers Example*

Heart Valve Replacement Study

  • Study information
    • Population: 256 patients receiving a valve replacement surgery, followed for up to 10 years from 1991–2002
    • Primary endpoint : All-cause mortality
    • Longitudinal biomarkers
      • Left ventricular ejection fraction (LVEF): < 50%
      • Valve gradient (mmHg): pressure difference across heart valve during blood flow (valve narrowing)
      • LV mass index (g/m\(^2\)): mass of LV relative to subject’s body surface area (hypertrophy)
    • Baseline factors
      • Patient age, sex, LV size (mm), LV function grade (1: good, 2: moderate, and 3: poor), history of cardiac surgery, presence of a coronary artery bypass graft (CABG), current use of ACE inhibitor, presence of high cholesterol, and operative urgency (0: elective, 1: urgent, and 3: emergency)

Data Format

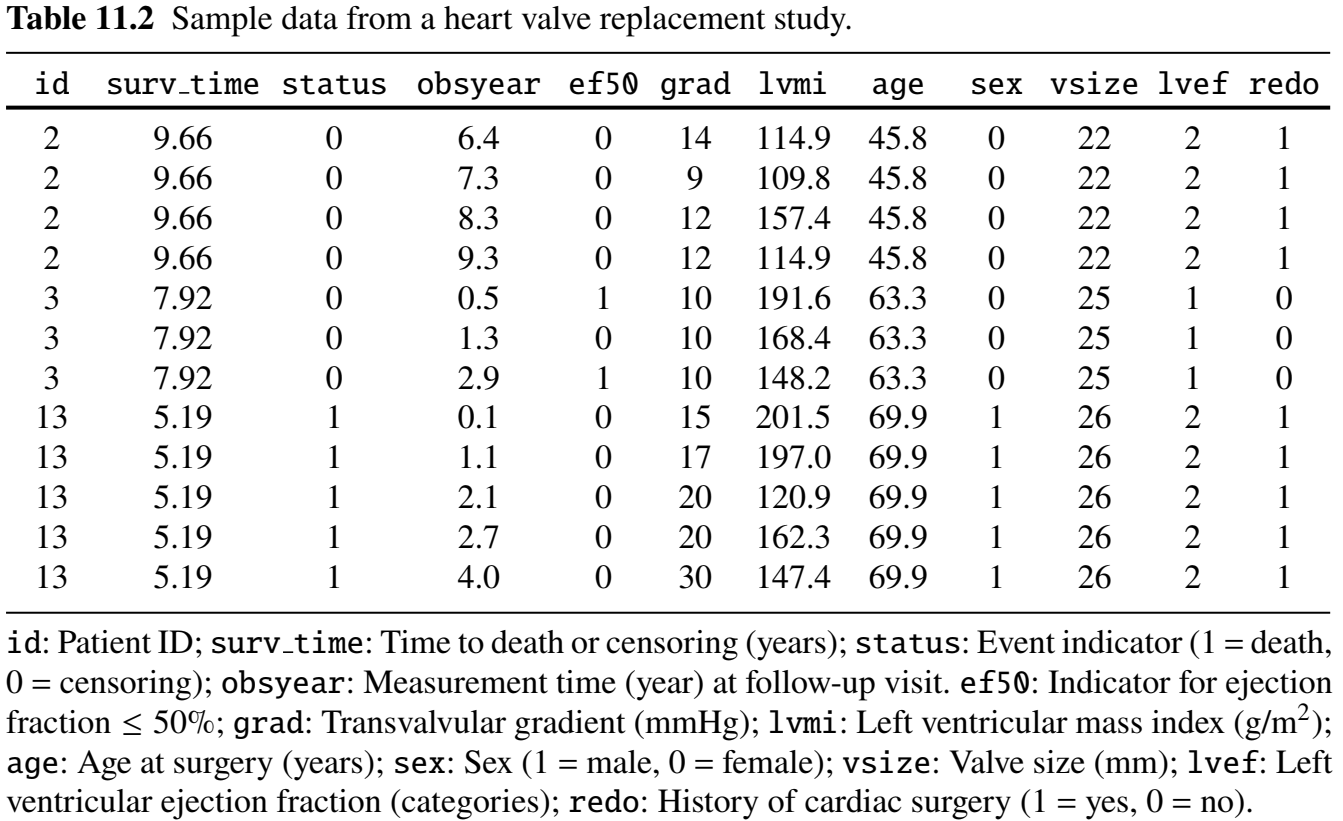
Longitudinal & Survival Sub-Models

  • Longitudinal sub-models
    • LVEF\(\le 50\%\): logistic GLMM (binary)
    • Valve gradient: LME (continuous)
    • LV mass index: LME (continuous)
  • Survival (Cox) sub-model
    • Current log-odds of LVEF\(\le 50\%\)
    • Current values and change rates of valve gradient and LVMI
    • Baseline age, sex

Model Fitting (I)

  • Longitudinal sub-models
# 1. Ejection fraction <= 50% at follow-up
ef_mod <- mixed_model(ef50 ~ obsyear + age + sex  + vsize + lvef + redo 
                      + cabg + acei + hc + emergenc, 
                      random = ~ obsyear | id, data = df,
                      family = binomial())

# 2. Valve gradient at follow-up
grad_mod <- lme(grad ~ obsyear + age + sex  + vsize + lvef + redo 
                + cabg + acei + hc + emergenc, 
                random = ~ obsyear | id, data = df)

# 3. LV mass index at follow-up
lvmi_mod <- lme(lvmi ~ obsyear + age + sex  + vsize + lvef + redo 
                + cabg + acei + hc + emergenc, 
                random = ~ obsyear | id, data = df)

Model Fitting (II)

  • Join with survival sub-model
# Survival sub-model
df_surv <- df[!duplicated(df$id),] # de-duplicated data
surv_mod <- coxph(Surv(surv_time, status) ~ age + sex,  
                  data = df_surv)

# Set-up functional forms biomarkers in Cox model
fForms <- list(
  "grad" = ~ slope(grad) + value(grad),
  "lvmi" = ~ slope(lvmi) + value(lvmi)
)

# Fit joint model
obj <- jm(surv_mod, list(ef_mod, grad_mod, lvmi_mod), 
                time_var = "obsyear",
                functional_forms = fForms)

Regression Results (I)

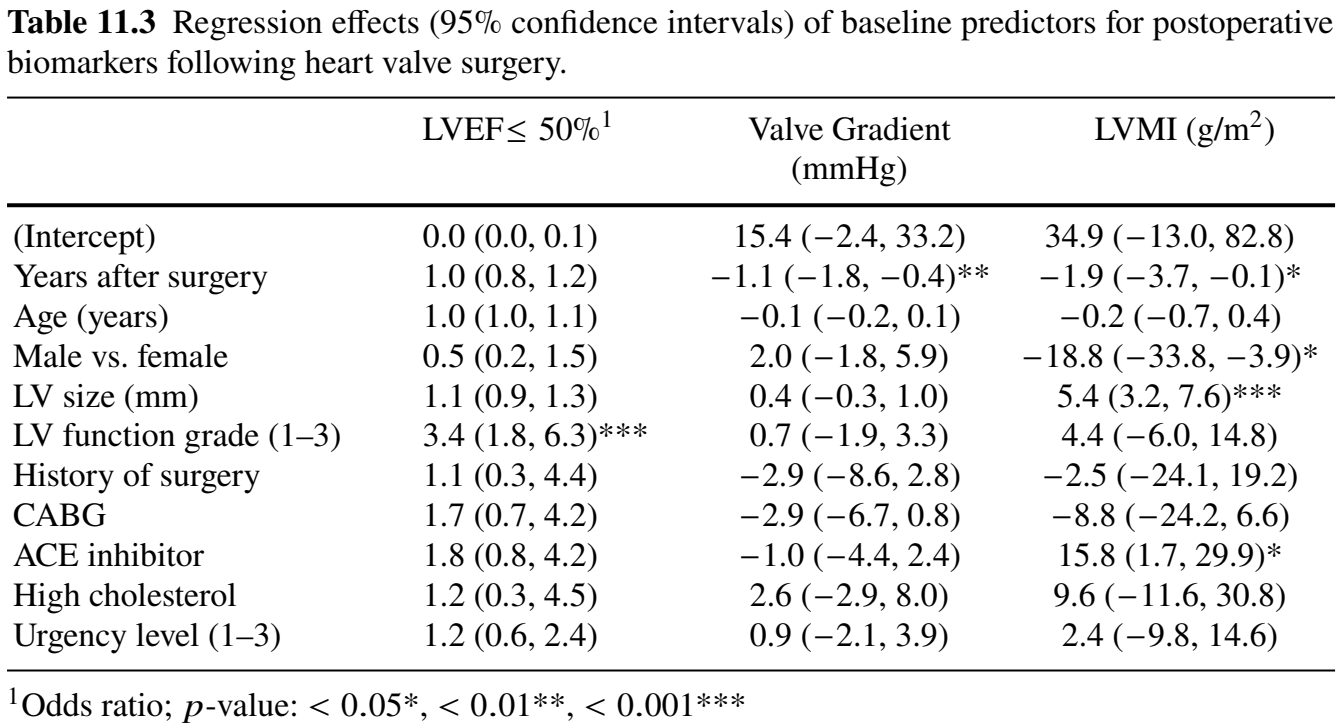
  • Three longitudinal sub-models

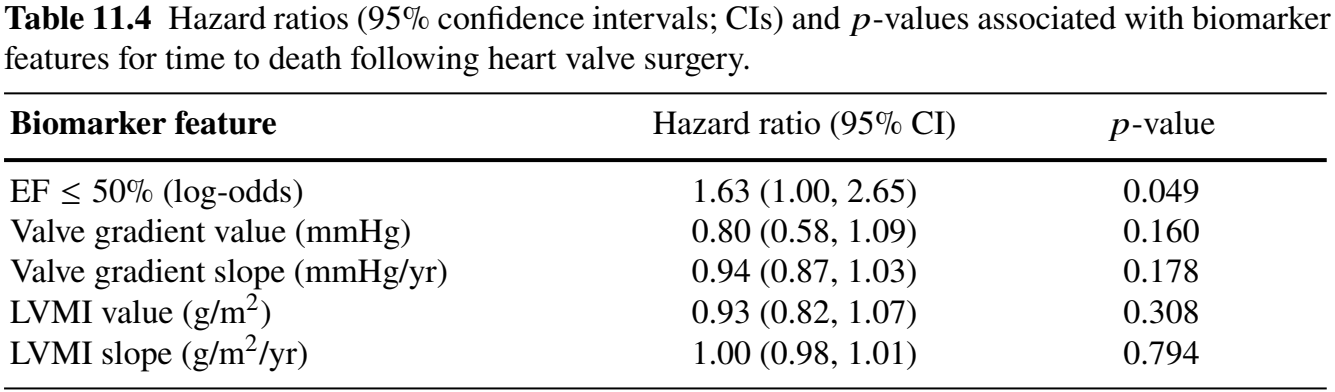
Regression Results (II)

  • Cox sub-model for mortality
    • Doubling odds of reduced LVEF \(\longrightarrow\) \(2^{1.63} - 1 = 210\%\) increase in mortality (\(p\)-value \(= 0.049\))

Prediction for Patient ID 3

  • Dynamic prediction: patient ID = 3 by year 3
# Set up data
t0 <- 3 # Set current time u
newdf <- df[df$id == 3, ] # Get data from patient 3
newdf <- newdf[newdf$obsyear < t0, ] # Subset to times before t0
# Indicate that the patient is alive at t0
newdf$status <- 0
newdf$surv_time <- t0
# Predict longitudinal trajectories
pred_longit <- predict(obj, newdata = newdf,
                       times = seq(t0, 10, length.out = 10),
                       return_newdata = TRUE)

# Plot the predicted trajectories
par(mfrow = c(1, 3))
plot(pred_longit, outcomes = 1:3, ...)

Prediction Results (I)

  • Biomarker trajectories

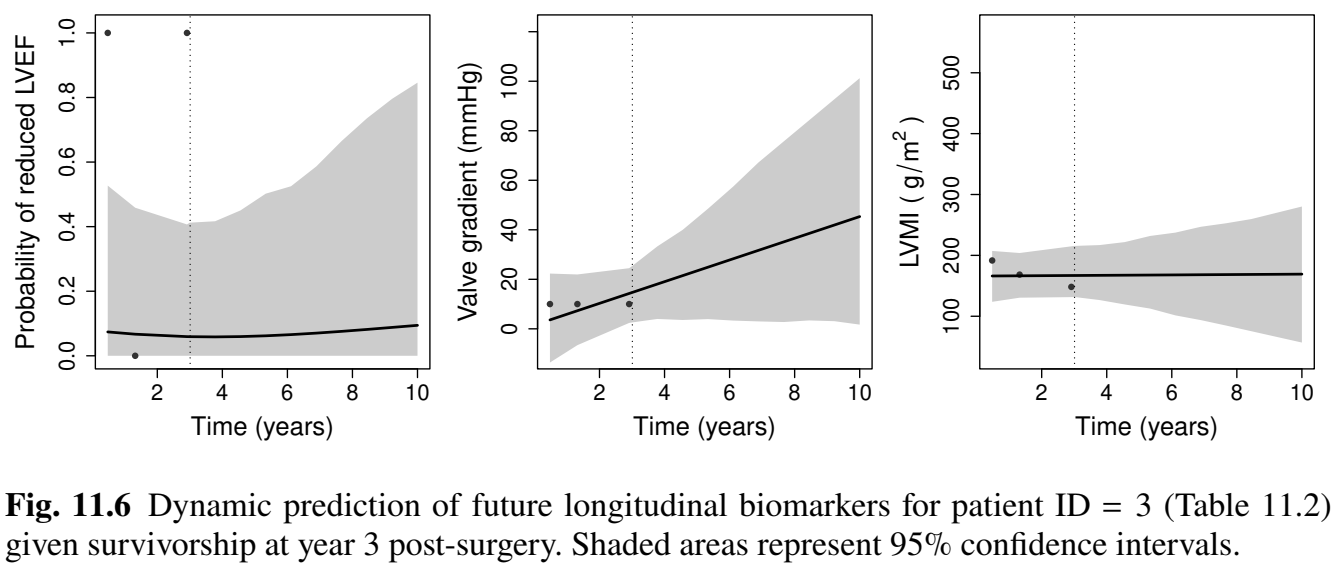
Prediction Results (II)

  • Predict survival curve
# Predict survival probabilities
pred_surv <- predict(obj, newdata = newdf, process = "event",
                     times = seq(t0, 10, length.out = 10),
                     return_newdata = TRUE)
# Plot the predicted survival probabilities
plot(pred_longit, pred_surv, outcomes = 1:3,
     fun_event = function(x) 1 - x, ...)

Prediction Results (III)

  • Predicted survival curve

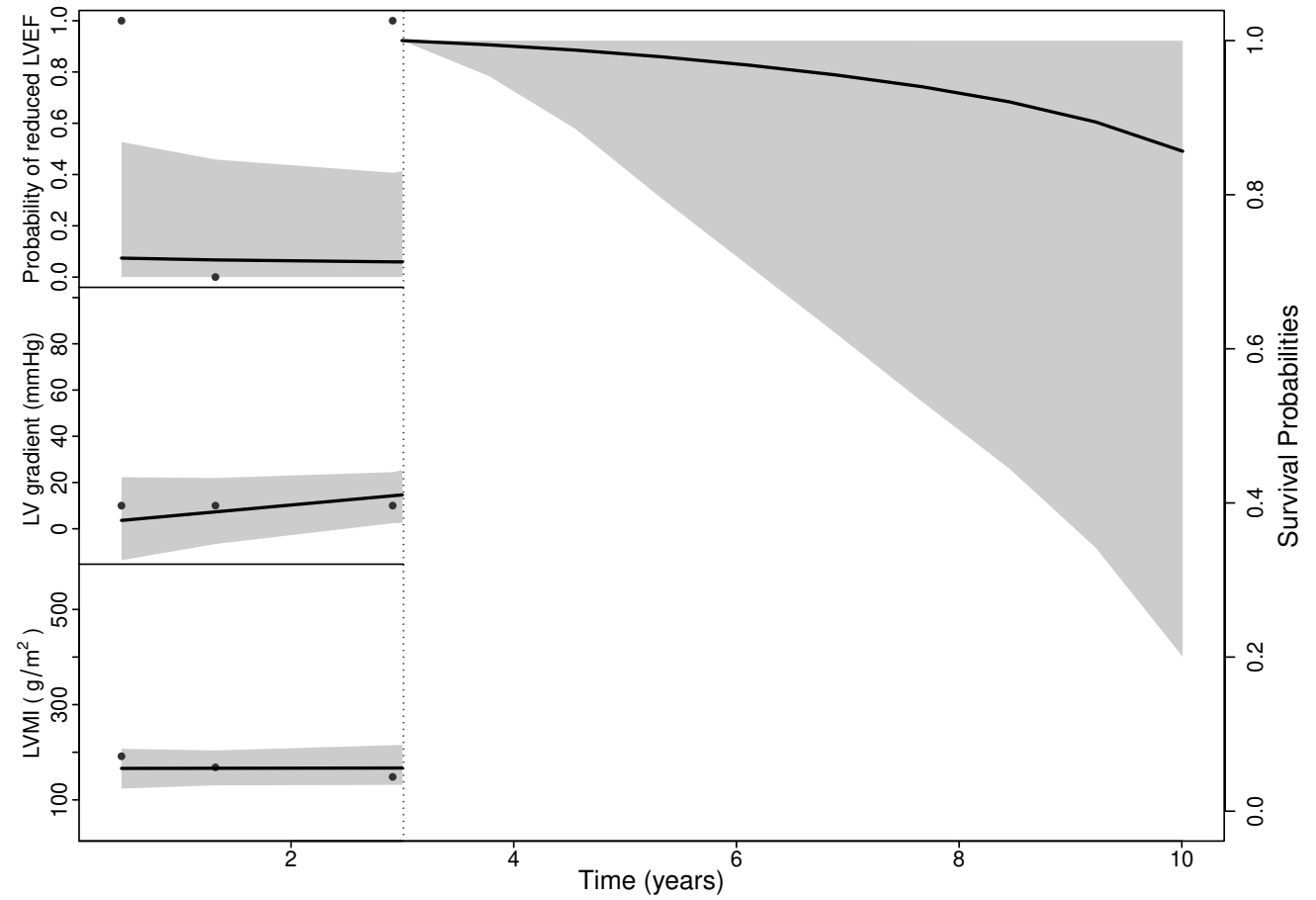
Conclusion

Notes

Summary (I)

  • Two-stage joint models
    • Longitudinal sub-model \[m_i(t)=\gamma_0+\gamma^\T Z_i(t)+b_i^\T\tilde Z_i(t)\]
      • obj1 <- nlme::lme()
    • Survival sub-model \[ \pr\{t\leq T_i<t+\dd t\mid Z_i^*, \overline m_i(t)\}=\exp\{\beta^\T Z_i^*+\nu m_i(t)\}\lambda_0(t)\dd t \]
      • obj2 <- survival::coxph()
    • Joining two models
      • JM::jointModel(obj1, obj2, timeVar)

Summary (II)

  • Extensions (Rizopoulos, 2012)
    • Biomarker \(\times\) baseline interactions
    • Change rate \(\to\) survival
    • GLME GLMM
    • Multivariate failure times (competing risks, recurrent events)
    • Dynamic predictions
    • JMbayes2 package for Bayesian approach
obj <- jm(surv_sub, list(longit_sub1, longit_sub2), 
          time_var = "obstime",
          functional_forms = fForms)