Applied Survival Analysis

Chapter 1 - Introduction

Author
Affiliations

Lu Mao

Department of Biostatistics & Medical Informatics

University of Wisconsin-Madison

Outline

  1. Time-to-event data and examples
  2. Censoring mechanisms and implications
  3. Summarizing the raw data

\[\newcommand{\indep}{\perp \!\!\! \perp}\]

Data and Examples

What are time-to-event data?

  • Common outcome type in medical studies
    • Starting point: Randomization, study entry, birth, etc.
    • Endpoint: Death, hospitalization, disease onset, etc.
    • In engineering: Machine failure times (reliability analysis)
  • Right censoring
    • Event does not occur by study end or dropout
    • Only know event time \(>\) censoring time
  • Survival analysis: Statistical methods for censored data

Example: Univariate event (I)

  • German Breast Cancer (GBC) Study
    • Population: 686 patients with node-positive breast cancer
    • Objective: Assess if tamoxifen + chemo reduces mortality
    • Baseline info: Age, tumor size, hormone levels, menopausal status, etc.
    • Follow-up: Median 44 months
      • 171 deaths \(\to\) exact times known
      • 515 censored \(\to\) survival time \(>\) censoring time

Example: Univariate event (II)

  • German Breast Cancer (GBC) Study

Example: Recurrent events (I)

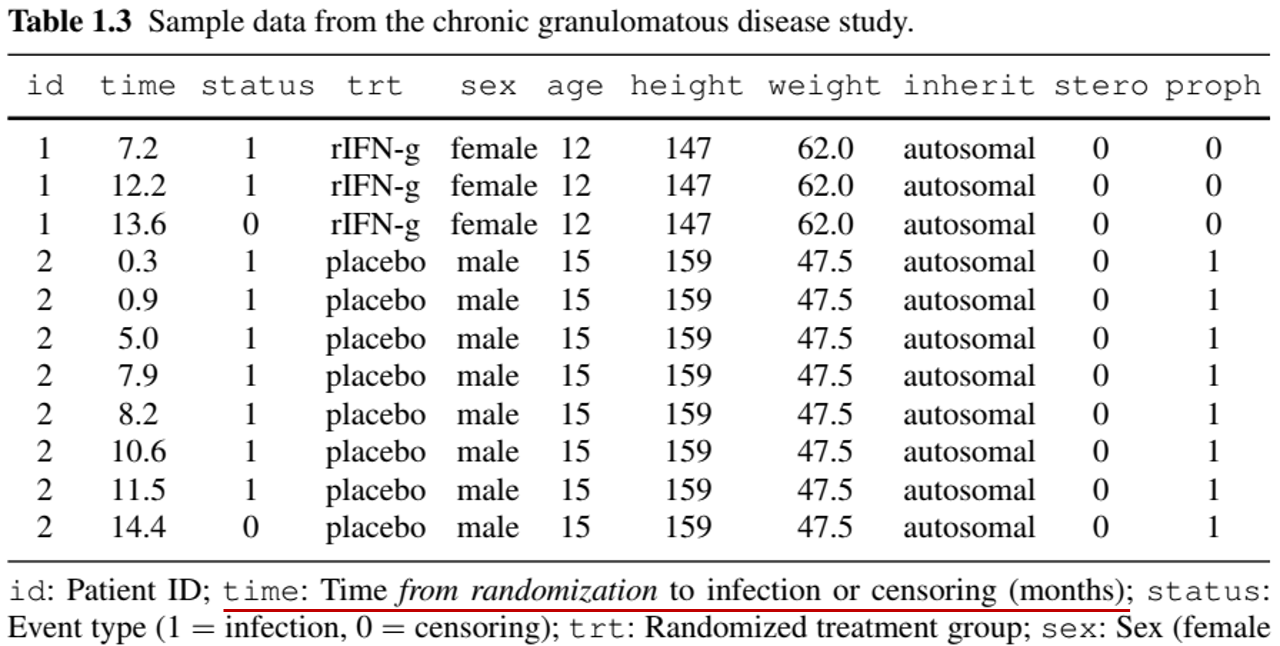
  • Chronic Granulomatous Disease (CGD) Study
    • Population: 128 patients in a randomized placebo-controlled trial
    • Objective: Assess gamma interferon effect on recurrent infections
    • Follow-up: Median 293 days
      • Infections: Min = 0, Max = 7
    • Challenge: Correlated events within individuals
    • Data in “long” format (multiple records per patient)

Example: Recurrent events (II)

  • Chronic Granulomatous Disease (CGD) Study

Example: Multivariate/Clustered Events (I)

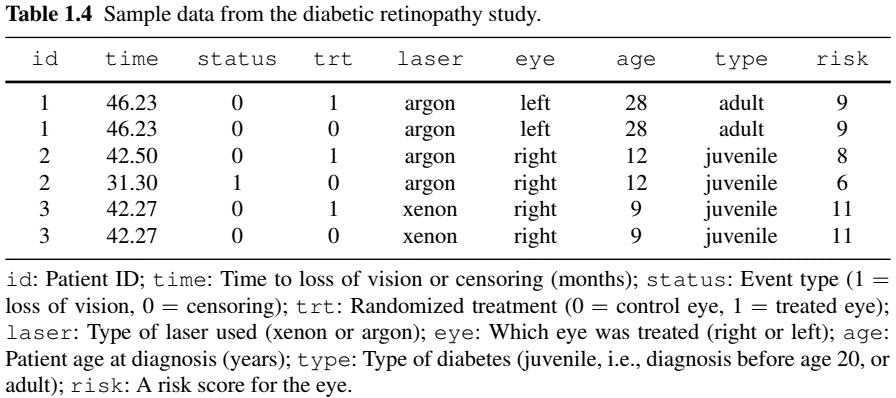
  • Diabetic Retinopathy Study
    • Population: 197 high-risk diabetic patients in a randomized controlled trial
    • Objective: Determine if photocoagulation (a laser treatment) delays blindness onset
    • Design: One eye treated (by either xenon or argon), the other untreated (control)
    • Challenge: Correlation between eyes

Example: Multivariate/Clustered Events (II)

  • Diabetic Retinopathy Study

Example: Competing Risks (I)

  • Definition: Multiple types of events where one prevents the occurrence of the others
    • Natural example: different causes of death
  • Competing risk vs censoring:
    • Both terminate follow-up
    • Competing risk: part of the outcome; inference based on its presence
    • Censoring: irrelevant to outcome; inference based on its absence
  • Example: death from prostate cancer as main outcome
    • Death from other (metastasized) cancers \(\to\) competing risk
    • Death from traffic accidents \(\to\) censoring

Example: Competing Risks (II)

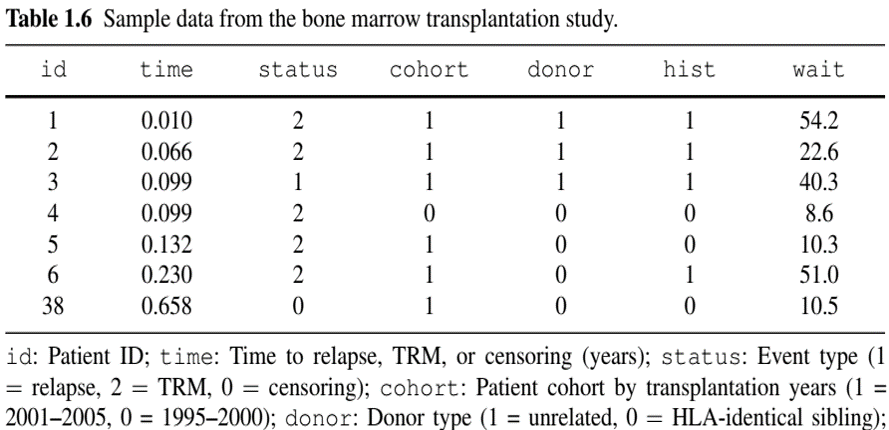
  • Bone Marrow Transplant Study

    • population: 864 multiple-myeloma leukemia patients undergoing allogeneic haematopoietic cell transplantation (HCT)
    • Objective: Evaluate risk factors for treatment-related mortality (TRM) and relapse of leukemia
    • Competing risks: TRM defined as death in remission (i.e., before relapse); thus is precluded by relapse
    • Risk factors: cohort indicator (years 1995–2000 or 2001–2005), type of donor (unrelated or identical sibling), history of a prior transplant, time from diagnosis to transplantation (<24 months, or ≥ 24 months)

Example: Competing Risks (III)

  • Bone Marrow Transplant Study
    • Why only one record per patient?

Example: More Complex Outcomes (Semi-competing risks)

  • German Breast Cancer (GBC) Study
    • Nonfatal event + terminal event (death)

Example: More Complex Outcomes (with Longitudinal data)

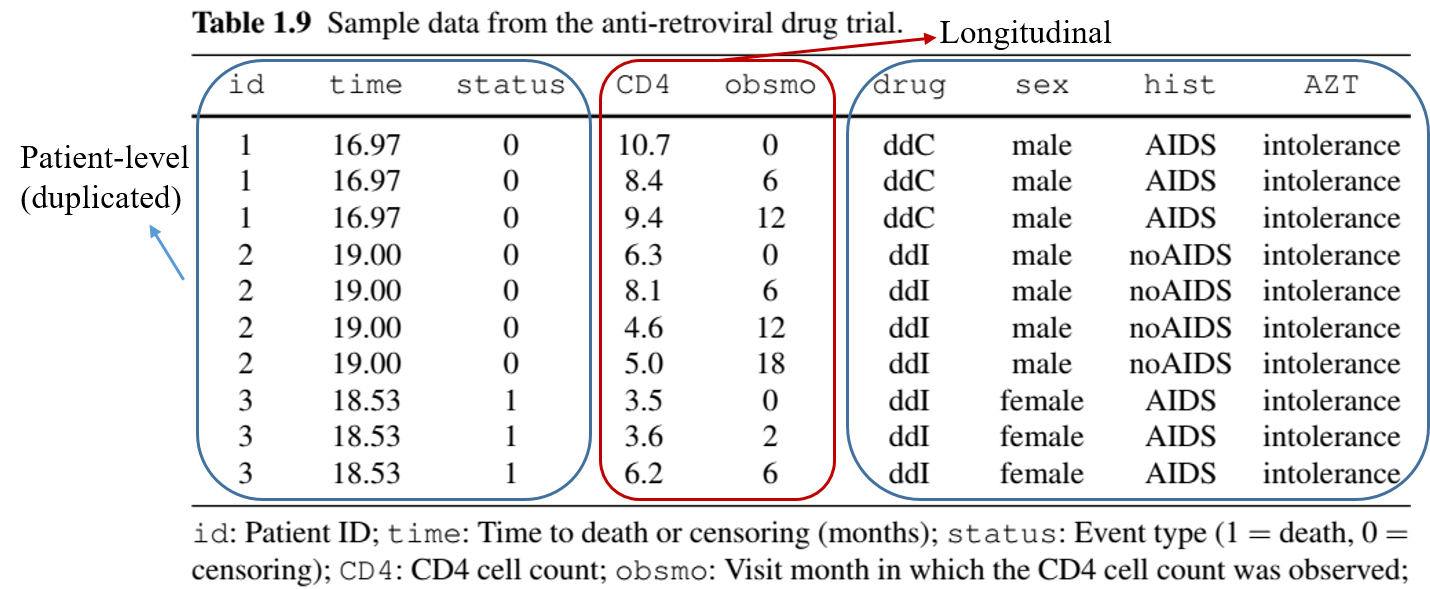
  • Anti-Retroviral Drug Trial
    • Repeated measures of CD4 cell count + death

Example: More Complex Outcomes (Multistate process)

  • Breast Cancer Life History Study
    • Remission \(\to\) relapse \(\to\) metastasis \(\to\) death (can skip states)

Example: Composite Endpoints(I)

  • Composite endpoint: one with multiple components
    • Recurrent/multivariate events
    • (Semi-)Competing risks
    • Longitudinal measurements
    • Multistate processes
  • Analysis of complex outcomes
    • Marginal approach: models components separately
    • Conditional approach: models components jointly
    • Composite approach: combines components
      • Progression/relapse-free survival (time to the earlier of progression/relapse or death)

Example: Composite Endpoints(II)

  • Advantages:
    • Concentrates information \(\to\) Statistical efficiency
    • No need for multiple testing adjustment
    • A single measure of overall effect size
  • Preferred for primary analysis of Phase-III clinical trials by
    • US Food and Drug Administration (FDA)
    • ICH (International Council for Harmonisation for pharmaceuticals)
  • Challenges:
    • Statistical efficiency (e.g., beyond first event)
    • Scientific relevance (e.g., relative importance of components)

Censoring mechanisms and implications

Censoring Mechanisms

  • Two mechanisms
    • Study termination (administrative censoring)
    • Loss to follow-up (LTFU, e.g., withdrawal, death from other causes)
Caution about censoring

  • Event/censoring time \(=\) time from starting point (e.g., randomization) to event/censoring (as opposed to time on the calendar)

  • LTFU may not be independent of outcome (e.g., sicker patients withdraw early)

  • Collect withdrawal reasons if possible

  • Censoring or competing risk? \(\leftarrow\) Domain knowledge

Censoring Mechanisms: Illustration

  • Calendar time vs time synchronized by starting point

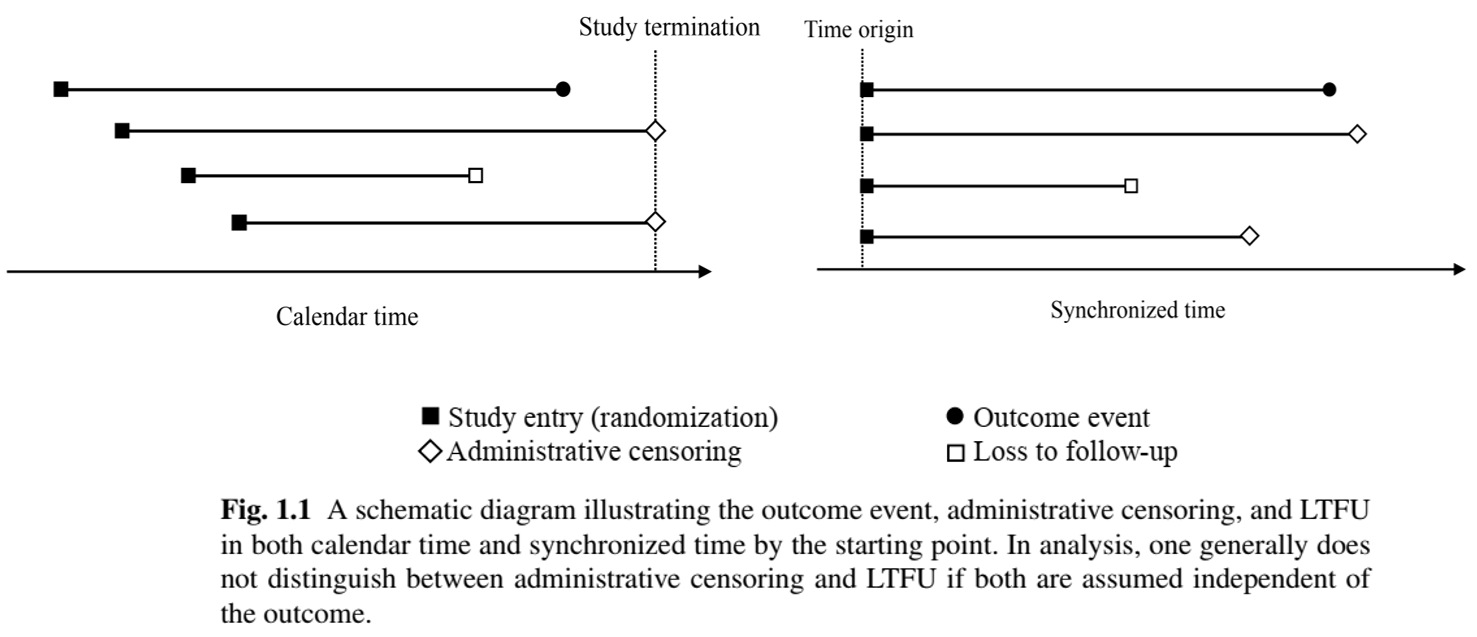
Statistical Implications (I)

  • Censored observation
    • Not completely missing!
    • Partial information: event time \(>\) censoring time
    • Ignoring partial information \(\to\) Bias in inference
  • Naive approaches
    • Treat censoring as event \(\to\) Underestimates time to event
    • Exclude censored observations \(\to\) Underestimates time to event (longer event times more likely censored)

Statistical Implications (II)

  • Notation

    • \(T\): Outcome event time
    • \(C\): Censoring time
    • Observed data: \(X=\min(T, C)\), \(\delta = I(T\leq C)\)
      • (𝑋, 𝛿) = (time, status) in previous data examples

  • Estimation

    • Independent censoring assumption

    \[ C \indep T\]

    • Estimand: \(S(t)={\rm pr}(T > t)\), i.e., probability of subject “surviving” to time \(t\), using a random sample of \((X_i, \delta_i)\) \((i=1,\ldots, n)\)

Statistical Implications (III)

  • Naive methods

    • Event-imputation empirical survival function: \[\hat S_{\rm imp}(t)=n^{-1}\sum_{i=1}^n I(X_i > t) \to {\rm pr}(X > t)\leq S(t)\]

    • Complete-case empirical survival function: \[\hat S_{\rm cc}(t)=\frac{\sum_{i=1}^n I(X_i > t, \delta_i = 1)}{\sum_{i=1}^n\delta_i} \to {\rm pr}(T > t\mid T\leq C)\leq S(t)\]

    • Both naïve methods underestimate the true survival function

Statistical Implications: Example

  • German Breast Cancer (GBC) Study

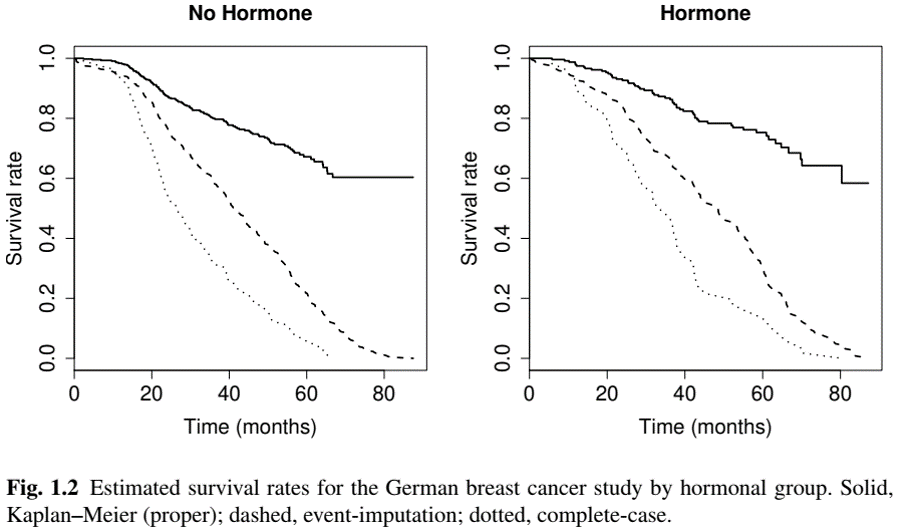
Summarizing Raw Data

Importance of Descriptive Analysis

  • Statistical models rely more or less on assumptions
  • Good practice to summarize data descriptively as first step
    • Get to know the data
    • Informs subsequent analysis
    • Check balance of baseline characteristics between randomized arms
    • “Table 1” in medical research papers
  • Two types of summary statistics
    • Subject-level characteristics (baseline variables, number of events per subject)
    • Event rates (over aggregate length of follow-up)

How to Calculate Event Rate (I)

  • Length of follow-up is event-specific
    • If an event is “non-recurrent”, its occurrence means patient is no longer at risk for it

Note

Denominator is called person-year (or person-time) of follow-up.

How to Calculate Event Rate (II)

  • Semi-competing risks

How to Calculate Event Rate (III)

  • Recurrent events

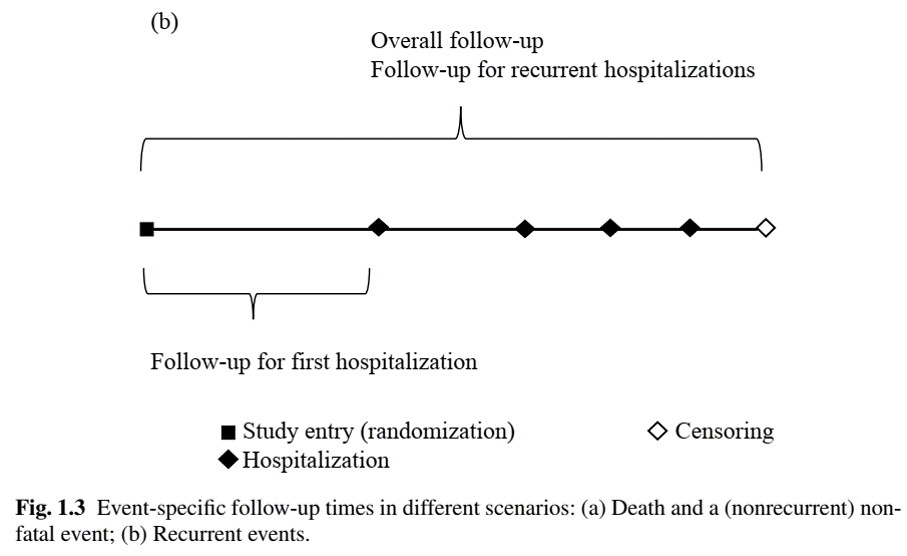
Table One: Example

Conclusion

Chapter Summary

  • Types of time-to-event outcomes
    • Univariate, recurrent, multivariate/clustered, (semi-)competing risks, repeated measures, multistate processes, and everything in between…
  • Common feature: censoring
    • Arises if study ends or patient drops out prior to event
    • Must be handled with care to avoid false conclusion
  • Importance of descriptive analysis
    • Event rate \(\to\) attention to denominator

HW1 (Due Feb 5)

  • Choose one
    • Problem 1.1 (Recommended for PhD in Stats/BDS)
    • Problem 1.2
  • Problem 1.8 (Attach you annotated code)
  • (Extra credit) Problem 1.3

Guidelines for HW

  • Present a readable and coherent text to report your methods and results
    • Include numerical/graphical results only if they contribute to your narrative
    • All tables and figures should be properly titled/captioned, with informative labels/legends
    • Use full names instead of abbreviations/acronyms
      • E.g., “meno” \(\to\) “Menopause (yes v no)”; “est” \(\to\) “Estrogen (fmol/mg)”
    • Specify the unit of variable, e.g., “Age (years)”
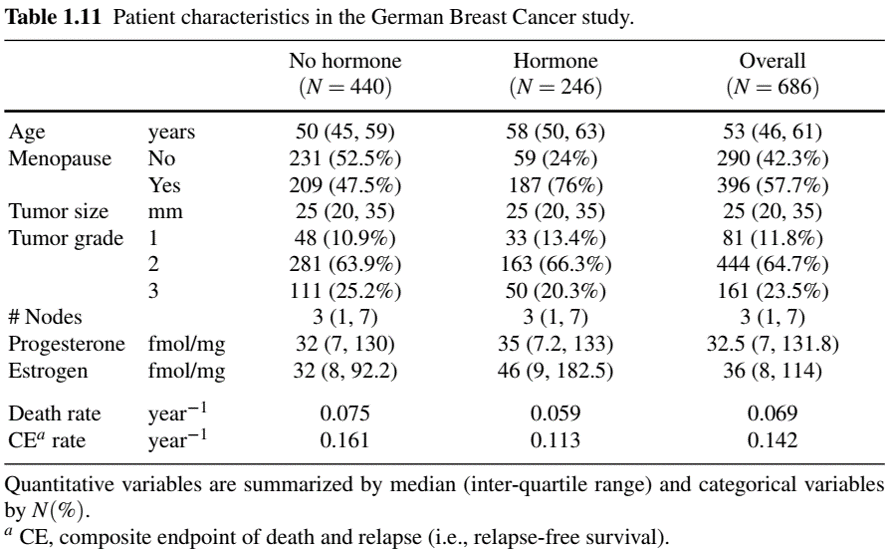
    • See Table 1.11 and Fig. 1.2 for examples
  • Append the full code for diagnostic purposes